Предельная себестоимость характеризует себестоимость C прироста продукции Q

(6)

Считая зависимость (5) непрерывной, естественно выражение (6) заменить точным выражением:

(7)

В экономике под предельной себестоимостью понимают именно эту производную. Применяют производные и в других случаях.

В анализе и прогнозах цен применяют понятие эластичности спроса. Пусть D = D (P)-функция спроса от цены товара P, тогда под эластичностью спроса понимают величину:

(8),

которую можно выразить и так:

(9)

II. Исследование функций с помощью производных.

Краткие сведения из теории.

При исследовании функций с помощью производных находят интервалы возрастания и убывания функции, интервалы выпуклости и вогнутости, точки перегиба графика функции, точки, в которых функция достигает экстремальных значений и характер экстремумов. При этом используют определения и теоремы.

Определение 1. Функция f(x) называется возрастающей в интервале (a, b) если для любых двух чисел x1 и x2 из неравенства x1> x2, следует неравенство f(x2)< f(x1), то функцию f(x) называют убывающей.

Замечание: Если из неравенства x1> x2 следует нестрогое неравенство , то функцию f(x) соответственно называют неубывающей или не возрастающей. Функции, возрастающие и убывающие, а также функции невозрастающие и неубывающие называют монотонными.

Теорема 1. (достаточный признак возрастания и убывания функции на интервале)

Если во всех точках некоторого интервала первая производная , то функция f(x) на этом интервале возрастает. Если же во всех точках некоторого интервала 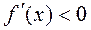, то функция f (x) на этом интервале убывает.

Пример: Определить интервалы возрастания и убывания функции

Решение: ОДЗ функции – вся числовая ось OX, ее производная . Для нахождения интервалов возрастания решаем неравенство:

> 0, а для нахождения интервалов убывания – неравенство: < 0.

Практически для решения задачи удобно, используя метод интервалов для решения неравенств, провести кривую знаков производной для всех интервалов на оси ОХ. Напомним, что такая кривая меняет знак при переходе через корень нечетной кратности производной (см. рис. 1)

Рис. 1 Кривая знаков

Из рис.1 следует, что на интервалах и ; на этих интервалах функция f(x) возрастает. На интервале (-1; 1) ; на этом интервале функция f(x) убывает.

Определение 2. Функция f(x) имеет в точке максимум, если ее значение в этой точке больше, чем ее значения f(x) во всех точках x, достаточно близких к , т.е.

Определение 3. Функция f(x) имеет в точке 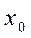минимум, если ее значение в этой точке меньше, чем ее значение f(x) во всех точках x, достаточно близких к 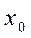, т.е.

Замечания: Максимум и минимум функции называют ее экстремумами.

1. Здесь и далее будем иметь в виду локальный экстремум, т.е. экстремум, достигаемый функцией в окрестности точки 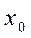. Вне рассматриваемой окрестности точки 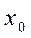функция может принимать большие или меньшие значения, чем в этой точке.

2. Функция f(x) может иметь несколько максимумов и минимумов; в этом случае может оказаться, что максимум в какой-либо точке меньше какого-либо ее минимума.

3. Функция f(x), определенная на отрезке, может достигать экстремума только во внутренних точках этого отрезка x. Это значит, что точки считаются экстремальными, если они имеют двустороннюю окрестность.

Теорема 2. (Необходимое условие экстремума)

Если функция f(x) имеет экстремум в точке 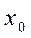, то ее производная в этой точке равна нулю или не существует.

Теорема утверждает, что точки экстремума следует искать только среди тех, в которых ее первая производная равна нулю или не существует. Такие точки называются критическими, если они входят в ОДЗ функции.

Указанный признак является только необходимым, но не является достаточным, так как производная может быть равна нулю или не существовать не только в тех точках, где функция имеет экстремум. Поэтому критические точки являются лишь «подозрительными» на экстремум и, найдя их, надо каждую из этих точек исследовать на экстремум отдельно с помощью достаточных признаков существования экстремума. Их две.

Теорема 3. (Первый достаточный признак экстремума)

Если при переходе слева на право через критическую точку 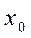функция f(x) первая производная функции меняет знак с плюса на минус, то - точка максимума; если же производная меняет знак с минуса на плюс, то - точка минимума функции f(x).

Если при таком переходе производная нем меняет знак, то экстремума в точке нет.

Теорема 4. (Второй достаточный признак экстремума)

Пусть ; тогда при функция f(x) имеет максимум, если и минимум, если .

Замечания: 1. Если в критической точке , то в точке экстремум может быть, но может и не быть.
В этом случае исследование надо проводить по первому достаточному признаку.

2. В точках графика функции, соответствующих максимуму или минимуму, касательная:

а) Может быть параллельна оси ОХ, если ; при этом экстремум имеет вид, изображенный на рис.2.

б) может быть параллельна оси OY, если (см. рис. 3)

в) если 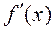не существует, то касательная не имеет определенного направления и экстремум имеет вид, изображенный на рис. 4.

		X0

Пример: Исследовать на экстремум функцию

Решение: Находим производную и приравняем ее нулю: .

Корни этого уравнения 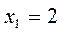и будут критическими точками. Так как всюду существует и конечна, то других «подозрительных» на экстремум точек нет. Представим производную в виде

И исследуем функцию на экстремум с помощью первого достаточного признака (см. теорему 3).

1) Исследуем точку 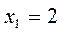. Рассмотрим знаки в окрестности этой точки , где и достаточно мало, например , тогда

Так как при переходе через точку 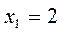слева на право меняет знак с «+» на «-», то в этой точке функция имеет максимум.

2) Исследуем точку

Отсюда следует, что в точке - минимум.

Замечание: Исследуя второй достаточный признак экстремума (см. теорема 4.) получим:

1) В точк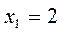е , в точке 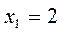функция имеет максимум,

2) В точке , функция имеет минимум,
С точки зрения трудоемкости вычислений, второй вариант решения представляется более предпочтительным. Применение второго достаточного признака, по-видимому, рациональней, чем применение первого, если вторая производная легко вычисляется и не является громоздким выражением. С другой стороны если первая производная не существует в «подозрительной» на экстремум точке, то исследование возможно производить только с помощью первого достаточного признака экстремума.

Пример 2. Исследовать на экстремум функцию:

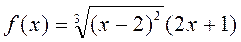
Решение: Находим производную.

Производная равна нулю при и не существует при . Исследуя эти точки с помощью первого достаточного признака, положив

1)
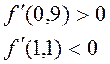
при переходе через точку меняет знак с «+» на «-», следовательно в этой точке функция достигает максимума.

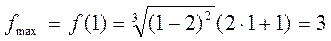
3) Аналогично находим, что при переходе через точку меняет знак с «-» на «+»:

Поэтому функция имеет минимум в точке

Важными характеристиками графика функции являются выпуклость и вогнутость дуг кривой и точками перегиба.

Определение 3. Говорят, что на интервале кривая вогнута если она лежит выше касательной, проведенной в любой ее точке и кривая выпукла, если она лежит ниже касательной, проведенной в любой ее точке.

Теорема 5. (Достаточное условие выпуклости и вогнутости)

Дуга кривой выпукла на интервале , если во всех точках этого интервала вторая производная функции 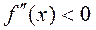и вогнута на этом интервале, если во всех его точках .

Из этой теоремы вытекает, что интервалы, в которых дуги кривой выпуклы, определяются из неравенства 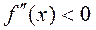, а интервалы в которых дуги этой кривой вогнуты, - из неравенства .

Определение 4. Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой, называется точкой перегиба кривой.

Определение 5. Точки из ОДЗ кривой , в которых 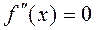или не существует, называются критическими точками второго рода.

Теорема 6. (Достаточное условие существования точки перегиба.)

Если или не существует, и при переходе через точку вторая производная меняет знак, то точка кривой с абсциссой есть точка перегиба графика функций .

Из теоремы 6 вытекает, что для нахождения точек перегиба кривой надо определить все критические точки второго рода и рассмотреть знаки в каждом из двух соседних интервалов, на которые эти точки делят область существования функции. В случае, если знаки в двух соседних интервалах различны, критическая точка второго рода, разделяющая эти интервалы, является абсциссой точки перегиба. В противном случае точки перегиба нет. В точке перегиба кривая пересекает касательную.

Пример: Найти интервалы выпуклости и вогнутости, а также точки перегиба графика функции.

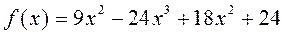
Решение: Находим производные

Функция и ее производные определены на всей числовой оси ОХ, причем в точке и обращается в нуль. Таким образом, вся ОДЗ функции разбивается этими точками на три промежутка 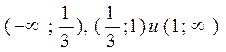. Проводя кривую знаков , получим:

Рис. 5

на интервалах и на интервале . Отсюда заключаем, что кривая на интервалах вогнута, а на интервале выпукла. При переходе, через точки и меняет знак, что в силу теоремы 6 означает: точки и являются абсциссами точек перегиба графика функций .