Цикл Карно

Анализируя формулу (3.3), можно заметить, что η _t возрастает при уменьшении q ₂ или увеличении q ₁. Отсюда можно заключить что, выбирая соответствующим образом процессы расширения и сжатия, протекающие с подводом и отводом теплоты q ₁, q ₂, можно изменять величину кпд. В связи с этим возникает вопрос - можно ли найти такой цикл, который обладал бы наибольшим кпд?

Такой цикл был предложен Сади Карно. Он состоит из двух обратимых изотермических и двух обратимых адиабатных процессов (см. рис.3.2, 3.3).

Рис. 3.2 Рис. 3.3

Изотермический и адиабатный процессы являются самыми выгодными процессами в смысле получения работы, т.к. в изотермическом процессе вся теплота, подводимая к рабочему телу, превращается в работу, а адиабатный процесс протекает без теплообмена.

Рассмотрим все процессы цикла Карно. Процесс 1-2 представляет про­цесс изотермического расширения рабочего тела с подводом теплоты q ₁ от верхнего источника теплоты с температурой T ₁. Количество теплоты q ₁, равное работе l ₁, полученной в процессе 1-2, определяется по формуле (см. § 4.4 – изотермический процесс).

Работа l ₁ определяется также площадью фигуры v ₁-1-2- v ₂ (см. рис.3.2.).

Процесс 2-3 является процессом адиабатического расширения. Газ со­вершает работу, численно равную площади фигуры v ₂-2-3- v ₃ и определяе­мую по формуле (см. адиабатный процесс § 4.5).

где k - показатель адиабаты.

В процессе 3-4 происходит изотермическое сжатие рабочего тела с отво­дом теплоты q ₂ к низшему источнику теплоты с температурой Т ₂. На сжатие затрачивается работа l ₃, численно равная площади фигуры v ₄-4-3- v ₃, равная количеству отведенной теплоты q ₂ и определяемая по формуле

В процессе адиабатного сжатия 4-1 газ нагревается до температуры T ₁. Работа, затрачиваемая на сжатие, численно равна площади фигуры v ₁-l-4- v ₄ и определяется по формуле

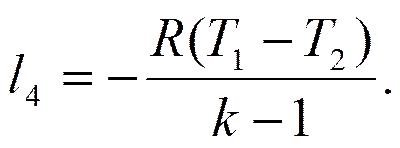
Если в процессе 3-4 сжимать газ, не охлаждая его (без отвода теплоты q ₂), то этот процесс будет адиабатным. Ввиду того, что адиабаты являются эквидистантными кривыми (не пересекаются между собой), то через одну точку (точка 3) можно провести лишь одну адиабату. Тогда в результате та­кого сжатия процесс пойдет не по изотерме 3-4, а по адиабате 3-2. В исход­ное состояние рабочее тело должно быть возвращено лишь по изотерме, так как в изотермическом процессе на сжатие затрачивается наименьшее коли­чество работы. В итоге на сжатие в процессах 3-4 и 4-1 будет затрачено то же самое количество работы, которое было получено в процессах расшире­ния 1-2 и 2-3. Полезная работа цикла l _ц и кпд η _t будут равны нулю. Отсюда можно сделать вывод: для того, чтобы получить полезную работу, необходи­мо какую-то часть подведенной теплоты безвозмездно отдать в окружающую среду, то есть потерять.

Полезная работа l _ц цикла 1-2-3-4 определяется алгебраической суммой работ, полученных или затраченных в отдельных процессах цикла. Суммируя площади, выражающие работу газа в отдельных процессах цикла с уче­том знаков работы, получим

l _ц = пл. 1-2-3-4-1 = пл. v ₁-1-2- v ₃ + пл. v ₃-2-3- v ₄ - пл. v ₄-4-3- v ₃ – пл. v ₁-1-4- v ₄.

Суммируя формулы работ для всех процессов цикла, получим

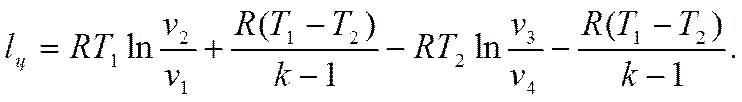(3.4)

Из полученной формулы видно, что работы в адиабатных процессах 2-3 и 4-1 взаимно уничтожаются. Тогда формула (3.4) примет вид

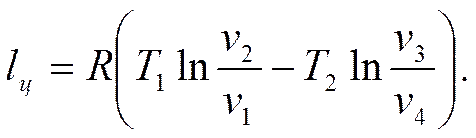
Коэффициент полезного действия любого цикла тепловой машины (в том числе и цикла Карно) определяется по формуле

Отсюда

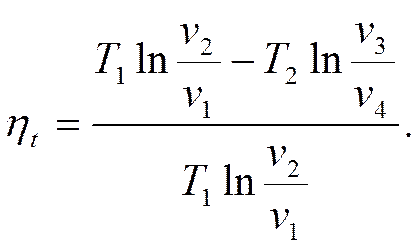(3.5)

Для адиабат 2-3 и 4-1 справедливы следующие зависимости

После деления первого уравнения на второе получим

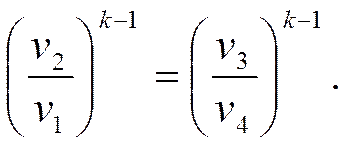
Логарифмируя последнее соотношение, будем иметь

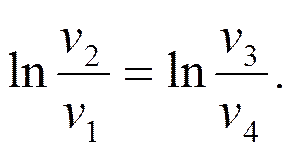(3.6)

Формула (3.5), учитывая (3.6), примет вид

(3.7)

Анализируя формулу (3.7), приходим к выводу, что η _t может быть равен единице лишь в случаях, когда T ₁→ ∞, либо T ₂=0 К. Эти условия невозмож­но осуществить даже в идеальном цикле, так как температура верхнего ис­точника теплоты T ₁, равная бесконечности, практически недостижима, а также и недостижима температура нижнего источника теплоты T ₂, равная абсолютному нулю температур T ₂=0 K=-273, 15 ⁰C.

Из формулы (3.7) также следует, что при Т ₂= T ₁ η _t=0. Это означает невоз­можность превращения теплоты в работу в случае равенства температур верхнего и нижнего источников теплоты. Отсюда можно дать еще одно оп­ределение вечного двигателя второго рода (первое определение было дано в § 3.3), являющееся также одной из формулировок второго закона термоди­намики (формулировка Оствальда): " Вечным двигателем второго рода назы­вается тепловой двигатель, с помощью которого можно было бы получать полезную работу в случаях, когда нет разности температур ". Согласно вто­рому закону термодинамики такой тепловой двигатель невозможен.

Анализ цикла Карно позволяет сделать также следующий важный вывод - невозможно превращение теплоты в работу без компенсации. Трудность усвоения формулировок второго закона термодинамики, содержащих поня­тие компенсации, связана со сложностью самого этого понятия.

Необходимо учитывать, что различают компенсацию двух родов. Ком­пенсация первого рода имеет место в случае, когда процесс превращения те­плоты в работу сопровождается изменением термодинамического состояния рабочего тела. Например, при изотермическом расширении идеального газа внутренняя энергия его, как известно, остается постоянной, и вся теплота, сообщаемая газу, превращается в работу. Увеличение объема газа, пред­ставляющее компенсацию первого рода, является здесь необходимым усло­вием превращения теплоты в работу.

В случае, когда превращение теплоты в работу влечет за собой изменение состояния не только рабочего тела, но и других тел, имеем компенсацию второго рода. В тепловых машинах такими телами обычно являются НИТ.

Что такое компенсация второго рода, наиболее просто понять из следую­щей формулировки второго закона термодинамики (формулировка Планка): " Невозможно построить периодически действующую тепловую машину, ко­торая не производила бы ничего другого, кроме поднятия груза и охлажде­ния источника тепла ".

Из этой формулировки следует, что для превращения теплоты в работу недостаточно одного только процесса передачи теплоты от ВИТ к рабочему телу. По второму закону термодинамики здесь предполагается наличие неко­торого дополнительного процесса. Для теплового двигателя таким дополни­тельным процессом является передача теплоты к НИТ. Этот дополнитель­ный процесс и представляет компенсацию второго рода.

В природе существуют процессы, которые могут протекать самостоятель­но, без сопровождения их другими процессами (без компенсации). Такие процессы являются самопроизвольными, естественными или некомпенсиро­ванными.

Примером самопроизвольного процесса может служить процесс превра­щения работы в теплоту при трении, который может протекать без сопрово­ждения его какими-либо другими процессами - без компенсации. Работа здесь полностью превращается в теплоту, тогда как процесс превращения те­плоты в работу, являющийся обратным по отношению к прямому процессу превращения работы в теплоту, нельзя провести без компенсации. Такие процессы, которые не могут протекать без того, чтобы вместе с ними не про­текал какой-либо дополнительный процесс, считаются не самопроизвольными.