Локальная структура обобщенных функций.

Лемма 1: 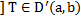- сужение обобщенной функции из . Для функции . Тогда для некоторого имеет место неравенство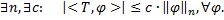

Лемма 2: 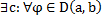справедлива оценка: .

Теорема (о локальной структуре обобщенных функций): 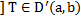- сужение обобщенной функции 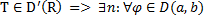справедливо представление .

Пояснение к теореме: . Мы можем к добавить произвольный многочлен и от этого интеграл не изменится.

Доказательство: рассм. здесь взято из оценки

В силу леммы 2: . Пусть - функционал на Докажем, что - инъективно.

многочлен степени Но многочлен не является функцией с компактным носителем. Многочлен является функцией с компактным носителем только в случае => j – инъективно. Инъективность:

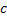. Левая часть неравенства – норма в . => S ограничен в смысле нормы в . S определен на подпространстве функции По теореме Хана-Банаха S продолжается до линейно ограниченного функционала на с сохранением . По теореме Рисса у нас имеется 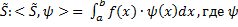из нашего подпространства.

Теорема доказана.