Фундаментальное решение.

Определение: Фундаментальным решением для дифференциального оператора L называется функция (читается как L примененная к G).

Теорема: Предположим, что функция является решением однородного дифференциального уравнения , удовлетворяющим следующим начальным условиям Тогда является фундаментальным решением для данного дифференциального оператора.

Доказательство: Применим Р к G:

. Докажем эту формулу: => получили исходную формулу.

@

….

@@

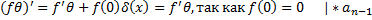
Сложим все равенства от @ до @@: . Теорема доказана.

Зачем нужно фундаментальное решение?

получили нужное решение

Рассмотрим неоднородное уравнение:

Предположим, что мы знаем фундаментальное решение для сдвига .

Тогда частное решение имеет вид

Замечание: Фундаментальное решение – решение неоднородного уравнения.