Носитель обобщенной функции. Структура обобщенной функции с точечным носителем.

Пусть - определена на .

Утверждение:

Следствие:

Определение: Носителем обобщенной функции называется , где - максимальное открытое множество, на котором

Примеры: 1) Пусть обобщ. функция - Дельта функция Дирака Её носитель – компактное множество.

2) Функция Хевисайда 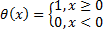. Её носитель - не компактное множество.

Теорема: (о структуре обобщенной функции с точечным носителем)

.

Доказательство: .

Открытый интервал . Рассмотрим Рассмотрим

По формуле Тейлора

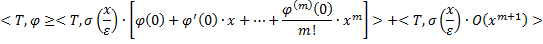
Первое слагаемое =

Возьмем и рассмотрим

Точно так же все выражения вида не зависят от .

первая сумма имеет нужный вид.

Докажем, что второе выражение =0.

. Эта оценка верна, так как .

Рассмотрим .

……. Везде получится .

|второе слагаемое| и второе слагаемое не зависит от второе слагаемое =0. Теорема доказана.