Приклад виконання завдання. Розглянемо приклад виконання завдання за наступних вихідних даних: авт./год; год; n = 5.

Розглянемо приклад виконання завдання за наступних вихідних даних: авт. / год; год; n = 5.

Розв’язок.

У випадку рівномірного закріплення автомобілів за кранами маємо одноканальних розімкнених СМО, до кожної з яких надходить потік вимог з інтенсивністю

авт. / год.

Використовуючи розрахункові формули для одноканальної СМО отримаємо:

1) інтенсивність обслуговування

авт. / год;

2) параметр завантаження системи (імовірність того, що кран зайнятий навантаженням)

;

3) імовірність того, що кран вільний від навантаження

;

4) середня тривалість очікування автомобілем початку навантаження

год.;

5) середня довжина черги автомобілів

автомобіля;

6) середня кількість автомобілів на контейнерному пункті

автомобілів.

Таким чином, біля кожного з кранів буде утворюватись черга довжиною автомобіля, що загалом становить на контейнерному пункті чергу з 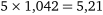автомобілів.

У випадку організації роботи пункту без закріплення автомобілів за кранами маємо одну п’ятиканальну СМО.

Використовуючи розрахункові формули для багатоканальної СМО отримаємо:

1) параметр завантаження системи

;

2) для виконання подальших розрахунків заповнимо розрахункову таблицю 9.3.

Таблиця 9.3 — Розрахунок багатоканальної розімкненої СМО

k	k!
				0, 0405	0, 2025
		3, 125	3, 125	0, 1266	0, 5063
		9, 766	4, 883	0, 1978	0, 5933
		30, 52	5, 087	0, 2060	0, 4120
		95, 37	3, 974	0, 1609	0, 1609
			18, 07		1, 875

3) імовірність того, що всі крани вільні від навантаження

;

4) імовірність того, що всі крани зайняті навантаженням

;

5) середня тривалість очікування автомобілем початку навантаження

год.;

6) середня довжина черги автомобілів

автомобілів;

7) середня кількість автомобілів на контейнерному пункті

;

8) середня кількість вільних від навантаження кранів (сума значень останнього стовпчика табл. 9.3)

.

Аналізуючи результати розрахунків бачимо, що у випадку організації роботи контейнерного пункту без закріплення автомобілів за кранами у порівнянні з варіантом закріплення автомобілів за кранами середня довжина черги зменшується з 5, 21 до 0, 447 автомобілів, а тривалість очікування зменшується з 0, 417 год. до 0, 036 год.

Контрольні запитання

1. Які задачі досліджує теорія масового обслуговування?

2. Дайте визначення каналу обслуговування та вимоги.

3. Назвіть особливості функціонування розімкненої системи масового обслуговування з очікуванням.

4. Перелічить вихідні дані, необхідні для розрахунку розімкненої СМО. За якої умови у системі не буде створюватись безкінечна черга?

5. Назвіть основні показники функціонування замкненої СМО.