
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Положення.
|
|
(Спосіб прямокутного трикутника)
Натуральна величина відрізка прямої загального положення дорівнює гіпотенузі прямокутного трикутника одним із катетів якого є проекція відрізка
на одну із площин проекцій, а другим катетом є різниця координат кінців відрізка (дивись другу проекцію). Кут між гіпотенузою і катетом-проекцією відрізка буде кутом нахилу відрізка до тієї площини проекцій, на якій ведеться побудова (рис. 2.8.)
Різниця координат кінців відрізка позначається значком ∆ (дельта) незалежно від координат х, у чи z.
Взаємне положення точки і прямої
Якщо точка А (наприклад) належить прямій b, то А2  b2, А1
b2, А1  b1, А1 і А2 розташовані на одній вертикальній лінії зв'язку. Можна сказати по іншому: Пряма b проходить через точку А (b
b1, А1 і А2 розташовані на одній вертикальній лінії зв'язку. Можна сказати по іншому: Пряма b проходить через точку А (b  А) (див. рис. 2.9.)
А) (див. рис. 2.9.)
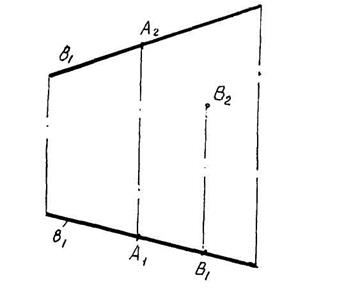
Взаємне положення точки і прямої використовується при діленні відрізка в даному співвідношенні, при визначенні положення відрізка в різних четвертях.
Точка В не лежить на прямій и (В1  b1, В2
b1, В2  b2)
b2)
Сліди прямої лінії
Сліди - це точки перетину прямої з площинами проекцій. Приклад на рис. 2.10.
Горизонтальний слід Н=b∩ П1. Для його побудови досить продовжити
фронтальну проекцію прямої (відрізка) до перетину з віссю Х12. b2∩ Х12=Н2.
Горизонтальна проекція Н1 знаходиться в результаті перетину продовження горизонтальної проекції прямої з вертикальною лінією, яка проходить через проекцію Н2. (Н1  b1).
b1).
Фронтальний слід F=b∩ П2. Для його побудови необхідно продовжити горизонтальну проекцію прямої (відрізка) до перетину з віссюХ12. b∩ Х12=F1; F2  b2. Горизонталі і фронталі мають один слід. Сліди прямих ліній використовують при побудові тіней елементів простору.
b2. Горизонталі і фронталі мають один слід. Сліди прямих ліній використовують при побудові тіней елементів простору.

Взаємне положення двох прямих
В просторі прямі можуть займати таке положення:
1. а ||b-прямі паралельні;
2. с∩ d -прямі перетинаються;
3. m _ n: - прямі мимобіжні.
Прямі а і b будуть паралельними коли однойменні проекції їх будуть паралельними. Тобто а||b, коли а1 ||b1, а2||b2 (рис. 2.11.)

Прямі, які мають одну спільну точку будуть перетинатися. А=с∩ d, коли А1=c1∩ d1, А2=с2∩ d2. Проекції А2 і А1 повинні лежати на вертикальній лінії зв'язку (рис. 2.12.).

Якщо прямі m і n не перетинаються і не паралельні, то вони будуть мимобіжними. Точки перетину їх однойменних проекцій не лежать на одній
вертикальній лінії зв'язку. На прикладі мимобіжних прямих (рис. 2.13.) визначимо видимість прямих за допомогою " конкуруючих" точок. Точка перетину фронтальних проекцій фактично відповідає двом точкам: (11  m1; 21
m1; 21  n1). Видима буде та точка, яка ближче до спостерігача (S). Точка 2, буде видимою, а точка 1 - ні. (проекція 12 взята в дужки). Аналогічно визначають видимість точок 3 і 4.
n1). Видима буде та точка, яка ближче до спостерігача (S). Точка 2, буде видимою, а точка 1 - ні. (проекція 12 взята в дужки). Аналогічно визначають видимість точок 3 і 4.
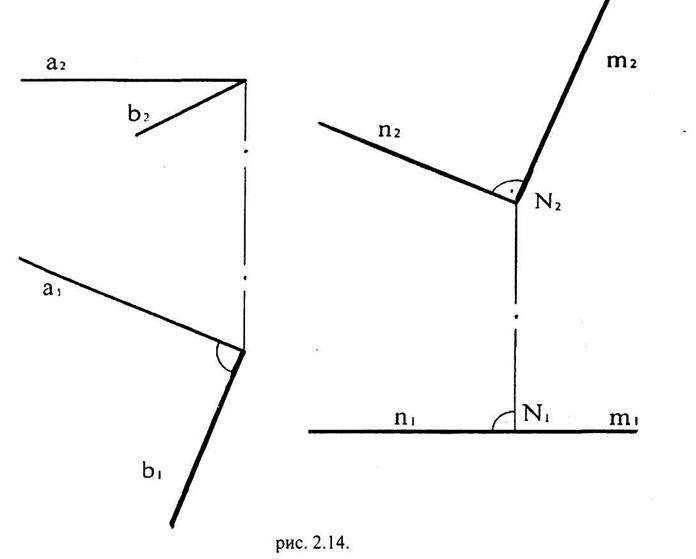
Проекції прямих кутів (окремі випадки)
Проекція прямого кута, утвореного двома прямими, які довільно розташовані в просторі, як правило, не прямий кут. Якщо ж одна сторона прямого кута паралельна одній із площин проекцій (рис. 2.14.), то на цю площину проекцій прямий кут буде проекціюватися в натуральну величину. Якщо обидві сторони прямого кута (чи будь якого кута) паралельні площині проекцій, то він також буде проекціюватися в Н.В. на цю П.
III. Площина. Точка і пряма на площині.

|
Задання площини на кресленні;
Площина утворюється рухом прямої твірної по прямій направляючій іаралельно заданому напрямку (рис. 3.1). Визначником площини називається сукупність кількості елементів, однозначно виділяючих дану площину з безлічі нших.