V. Комплексне креслення поверхонь.

Поверхні діляться не дві групи:

1 - багатогранні;

2 - криві.

Багатогранні - поверхні утворені частинами площин які перетинаються.

Тіло, обмежене багатогранною поверхнею називається, багатогранником.

Основні елементи багатогранної поверхні: грані, ребра та вершини.

Найбільш поширені багатогранники - призми і піраміди. Серед безлічі багатогранників в окрему групу виділяють правильні опуклі багатогранники, або тіла Платона. їх п'ять, у них усі ребра, грані, кути рівні між собою.

♦ Тетраедр - чотиригранник, гранями якого є чотири рівносторонніх трикутника.

♦ Октаедр - восьмигранник, гранями якого є вісім рівносторонніх трикутників.

♦ Ікосаедр - двадцятигранник утворений з двадцяти рівносторонніх трикутників.

♦ Гексаедр (куб) - шестигранник, гранями якого є шість квадратів.

♦ Додекаедр (дванадцятигранник) утворений з дванадцяти правильних п'ятикутників.

Задання пірамід та призм на комплексному кресленні.

Піраміда (рис. 5.1.) - багатогранник, у якого всі грані крім однієї (основи) мають спільну вершину. Оскільки всі грані піраміди - трикутники, піраміда визначається заданням її основи та вершини.

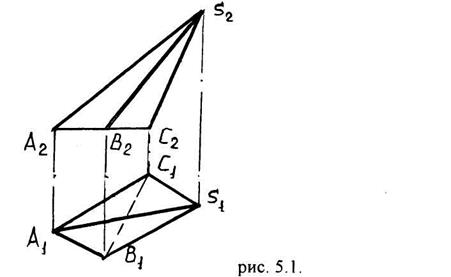
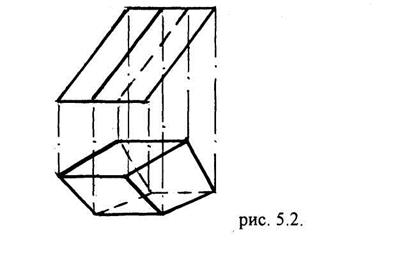
Призма (рис. 5.2.) - багатогранник, обмежений призматичною поверхнею та двома паралельними площинами (основами). Основами призми є рівні багатокутники, а бічні ребра рівні між собою. Коли основи призми не паралельні між собою, вона називається зрізаною. Якщо ребра призми

перпендикулярні до її основи призму називають прямою, коли ні - похилою. Призми та піраміди розрізняють за числом вершин основи. Коли основою призми чи піраміди є привильний багатокутник, а висота збігається з віссю, поверхню називають правильною.

Криві поверхні.

Сукупність послідовних положень тверної лінії, що переміщується по направляючій, утворюють поверхню Ф (кінематичний спосіб задання фігур) (рис. 5.З.), існують інші визначення.