
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Круги и квадраты человеческого сознания
|
|
Мы подойдем к третьей информационной системе непрямым путем.
По мере нашего продвижения будет проявляться источник, Плод
Жизни. Назовем эту новую систему круги и квадраты человеческо
го сознания. Китайцы называют ее квадратурой круга и окружением
квадрата.
Согласно Тоту, все уровни сознания во Вселенной объединены в Сакральной геометрии единым образом. Этот образ - ключ ко времени, пространству и измерениям, а также к самому сознанию. По словам Тота, даже эмоции и мысли основаны на Сакральной геометрии, но данная тема пока подождет и будет рассмотрена в этой книге позже.
Для каждого уровня сознания есть связанная с ним геометрия, которая полностью определяет, как этот конкретный уровень сознания ин-
|
| терпретирует одну Реальность. Каждый уровень - это геометрический образ или линза, сквозь которую смотрит дух, чтобы увидеть одну Реальность, получая совершенно уникальный опыт. Даже Духовная иерархия Вселенной геометрична по своей структуре, копируя в этом природу. Как сказал Тот, под Сфинксом находятся заключенные одна в другую девять хрустальных сфер. Археологи и ясновидящие давно уже ищут их - такова древняя легенда. Считается, что хрустальные сферы каким-то образом связаны с сознанием Земли и тремя уровнями сознания, которые сейчас свойственны человечеству. Поиском легендарных сфер занимались многие, они потратили на это огромное количество времени и денег, но, как говорит Тот, вам не нужны хрустальные сферы; вам надо только нарисовать девять концентрических кругов, потому что это точно так же все объясняет. Если бы люди знали, что искомым является сознание и геометрия, а не обязательно объект, то это знание могло бы прийти и раньше. Согласно Тоту, если бы вам предстояло приблизиться к планете, которую вы никогда раньше не видели, и узнать, какие уровни сознания существуют на ней, вам нужно было бы взять небольших существ с этой планеты и обмерить их, конечно, если допустить, что вы сумеете достаточно долго удерживать их в неподвижном состоянии. На основании измерений вы можете установить связанные с их телами сакральные пропорции квадрата и круга, а по этой информации определить точный уровень их сознания. Для определения уровня сознания «нечеловеческих» форм жизни, таких как животные, насекомые и внеземные существа, применяются другие пропорции, всегда выводимые из куба, но в случае с человеком - это круг и квадрат. Сравнив, что больше - квадрат или круг, описанные вокруг тела, и точно подсчитав насколько, - вы можете определить, как эти формы жизни интерпретируют Реальность и на каком уровне сознания они находятся. Есть, правда, и более быстрые способы определения, но данный способ фундаментален для самого существования. Тот велел нарисовать девять концентрических кругов и расположить вокруг каждого из них квадрат со стороной, равной диаметру круга, как на рисунке 9-1. Тем самым вы получаете уравновешенные мужскую и женскую энергии. Затем посмотрите, каким образом квадраты соотносятся с кругами, то есть как мужская энергия взаимодействует с женской. Согласно Тоту, самое главное в том, насколько периметр квадрата и длина окружности круга приближаются к пропорции фи. Это - ключ к человеческой жизни. Нахождение пропорций фи, близких к совершенным Глядя на внутренний квадрат, мы не видим пересекающих его кругов; это справедливо и для второго квадрата. Третий квадрат начинает пересекать четвертый круг, хотя очевидно, что это не пропорция фи. Однако четвертый квадрат пересекает пятый круг и между ними про- |
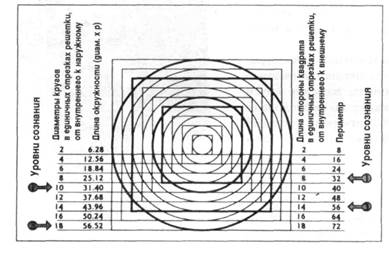
| Рис. 9-1. Концентрические круги и квадраты. Более темные круги и квадраты составляют пары, приближающиеся к пропорции фи. Они также задают расположение первого и третьего уровней человеческого сознания. (Единица измерения сети равна радиусу центрального круга или половине стороны окружающего его квадрата. Видно, что диаметр центрального круга и сторона описывающего его квадрата имеют одинаковую длину) |
| В этом томе вместо понятия Решетка Сознания Христа будет использовано понятие Сеть Сознания Христа, что является более точным по смыслу переводом английского эквивалента. - Прим, ред. |
является почти точная пропорция фи. На пятом и шестом квадратах изображение снова отклоняется от этой пропорции. Затем, неожиданно, седьмой квадрат пересекает девятый круг так, что вновь появляется почти точная пропорция фи, но не с одним кругом за его пределами, как это было в случае четвертого квадрата и пятого круга, а с двумя кругами. И соотношение становится еще ближе к Золотому сечению (равному 1, 6180339...), чем в первом случае.
Это начало геометрической прогрессии, которая может продолжаться бесконечно, прогрессии, где мы, люди - всего лишь вторая возможная ступень. (А мы так высоко себя ценим!) Если взять за единицу измерения продолжительность человеческой жизни, то мы сейчас находимся на уровне сознания, представленного развитием человеческой зиготы сразу после образования первой клетки. Жизнь во Вселенной превосходит все, что мы можем себе представить, но мы — это семя, содержащее в себе как начало, так и конец.
Если вернуться к практическому аспекту, то вы можете сделать все измерения даже без линейки, приняв радиус самого внутреннего круга за единичный отрезок. Первый круг и первый квадрат имеют поперечный размер в два радиуса. (Такими отрезками и создается применяемая здесь сеть*). И когда вы дойдете до четвертого квадрата, то в поперечнике он будет составлять 8 радиусов. Чтобы узнать число радиусов, составляющих все четыре стороны этого квадрата, вы просто умножаете их на 4, и тогда видно, что периметр четвертого квадрата составляет 32 радиуса. Нам надо знать периметр, потому что когда он будет равен или приблизится к длине окружности круга, мы получим пропорцию фи (см. главу 7).

|
Допустим, мы хотим посмотреть, равна ли (или близка ли) длина окружности пятого круга периметру четвертого квадрата (32 отрезка). Сначала определим длину окружности путем умножения диаметра круга на число пи (3, 14). Поскольку пятый круг в поперечнике составляет 10 единиц (радиусов), то, если вы умножите это на число пи (3, 14), длина окружности будет равна 31, 40 радиусам. Периметр квадрата равен точно 32, значит размеры круга и квадрата очень близки, но окружность чуть меньше. По Тоту, это соответствует моменту, когда человеческое сознание впервые начинает самоосознавать себя.
А теперь давайте проведем аналогичные расчеты для седьмого квадрата и девятого круга. В поперечнике седьмого квадрата 14 радиусов; умножение стороны на 4 дает нам 56 радиусов для периметра седьмого квадрата. Девятый круг имеет диаметр в 18 радиусов, и это число, умноженное на пи, есть 56, 52. Следовательно, в этом случае круг чуть больше квадрата, хотя до этого он был немного меньше. Если вы продолжите создавать круги за пределами девяти первоначальных, то увидите ту же картину: чуть больше, чуть меньше, чуть больше, чуть меньше — все больше и больше приближаясь к совершенству ряда Фибоначчи, стремящегося к пропорции фи (см. главу 8).
| Рис. 9-2. Первый и третий уровни человеческого сознания, почти совершенная пропорция фи |