
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Изъян в лестнице
|
|
До того, как я соединил два рисунка, 9-12 и 9-13, полученные из исходного рисунка Люси Лэми, я начал рисовать концентрические круги для каждой линии лестницы, кроме 20-й, как показано на рисунке 9-13а.
Обратите внимание, что на исходном рисунке (рис. 9-8) центральный круг был разделен ровно на пять горизонтальных составляющих, или ступенек лестницы (горизонтальную линию, идущую через середину круга, не считайте). Вы это ясно увидите. Поэтому я предположил, что и другие круги Плода Жизни надо также поделить ровно на пять частей. Довольно просто. Я так и сделал. Вот что получилось (рис. 9-14), если взять только три верхних вертикальных круга, опустив для упрощения остальные.
В каждом круге пять равных частей. Единственная проблема была в том, что это построение не годилось, оно не работало. Я не мог в это поверить! Я-то думал, что все будет так просто, и отсюда я пойду дальше, но ничего не получалось. Это построение не работало геометрически. Тогда я вернулся назад и проверил оба рисунка, уверенный, что не мог ошибиться. Оно там, это же ясно как день. Но когда я снова их соединил, они опять-таки не совмещались.
После многих, многих часов бесплодных попыток, я вернулся к тому, с чего начал, и принялся заново изучать исходный рисунок Люси. Определенно, в среднем круге было пять делений и по семь делений с каждой его стороны. Потом я раздобыл специальный небольшой прибор для измерения размера ступенек лестницы. Оказалось, что семь делений под и семь делений над центральным кругом были меньше тех, что находились внутри него! Люси изменила размеры, чтобы они подходили! Она знала, что мы находимся на негармоничном уровне сознания; она знала, что лестница не впишется, если не изменить некие параметры, но хотела все это поместить в одном рисунке. Поэтому она заставила лестницу вписаться, зная, что если люди исследуют ее, то они поймут, что уровень с 19 делениями, который она нарисовала, является негармоничным уровнем сознания.
Это был тонкий подход, подобный тому, как в каноне человека, в верхней части своего рисунка Леонардо сделал надпись в зеркальном отражении, чтобы вам пришлось держать зеркало для ее прочтения. Точно так же исходный рисунок Люси - это мужской аспект, а его женской составляющей является зеркальное отражение. Это как бы небольшая игра по сокрытию того, что вы не хотите сообщать внешнему миру. Словно внезапно прозрев, я и впрямь стал понимать, что наш уровень сознания действительно дисгармоничный, и египтяне тоже это знали. С той поры я стал намного больше времени проводить за изучением рисунков Люси.
|

|
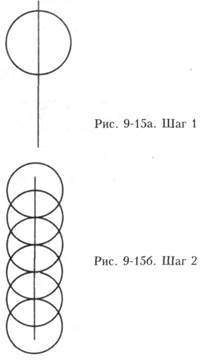
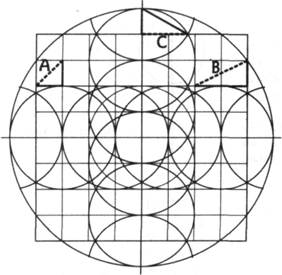
| Tpи линзы Теперь, зная, что египтянам были известны три уровня сознания, мы вернемся к тем трем геометрическим рисункам и тщательно их изучим. Это — линзы, которыми пользуется каждый уровень человеческого сознания для интерпретации Реальности: 8 на 10, 10 на 12 и 14 на 18. Начнем с прорисовки 8 на 10, первого уровня сознания. Тот показал мне гениальный способ построения этого рисунка без замеров и расчетов. Вам нужны лишь линейка и циркуль. Он сам показал мне, как это делается, сказав, что данный метод сбережет массу времени (см. инструкции внизу справа к рис. 9-15). Закончив последний шаг, вы имеете сеть из 64 квадратиков в большом квадрате и большой круг, выходящий за периметр большого квадрата ровно на одну ширину квадратика (рис. 9-16). Большой квадрат в поперечнике составляет 8 квадратиков, а большой круг 10 квадратиков - идеальные 8 на 10. И вам не нужна линейка! |
| 1. Проведите вертикальную линию, потом начертите на линии круг (рис. 9-15а) 2. Начертите еще пять идентичных кругов с центрами в точках, где вертикальная линия пересекает окружность предыдущего круга (рис. 9-156) 3. Проведите горизонтальную линию через точки среднего Весика Писцис. Из центра пересечения горизонтальной и вертикальной линий начертите большой круг, охватывающий четыре внутренних круга (рис. 9-15в) 4. Начертите круг того же размера, что на рис. 9-156, с центром в точке пересечения горизонтальной линии с окружностью большого круга. Начертите еще 5 кругов, как во втором шаге, но расположенных горизонтально (рис. 9-15г) 5. Постройте квадрат в пропорции фи, стороны которого проходят через длинные оси четырех внешних Весика Писцис 6. Внутри квадрата проведите параллельные линии через каждую точку касания окружностей (где круги касаются, но не пересекаются), а также через длинные оси каждой из оставшихся Весика Писцис (рис. 9-16). Так вы получите сеть 8 на 10 |
|
| Рис. 9-17а. Корень квадратный из 2гх (треугольник А), корень квадратный из 5-ти* (треугольник В) и корень квадратный из 3-х (треугольник С) Примечание, Теорема Пифагора соотносит гипотенузу треугольника с его сторонами: h2 = а2 + b2 или h = V а2 + b2, где h — гипотенуза, а и b — стороны треугольника * Так, при а = 2, а b = 1 (как в треугольнике В) а2 + b2 = 5 и h = V 5 |