Сформулировать и доказать теорему о связи смешанного произведения с объемом параллелепипеда

Найдем по определению смешанное произведени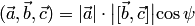е: , где 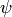— угол между векторам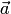и и . Модуль векторного произведения (по геометрическому свойству 1) равен площади параллелограмма, построенного на векторах 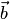и 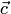:. Поэтому . Алгебраическое значение 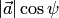длины проекции вектора 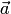на ось, задаваемую вектором , равно по модулю высоте 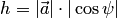параллелепипеда, построенного на векторах (рис. 1.47). Поэтому модуль смешанного произведения равен объему 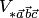этого параллелепипеда:

Записать условие компланарности векторов

Три вектора компланарны если их смешанное произведение равно нулю.

25. Вывести способ вычисления смешанного произведения в координатах

Покажем, как находится смешанное произведение, если известны координаты умножаемых векторов в прямоугольной системе координат. Пусть 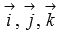- координатные векторы.

Векторное произведение в координатах имеет вид

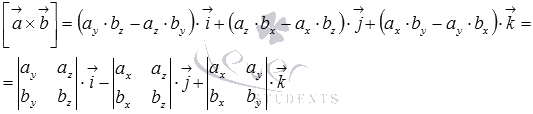
а скалярное произведение векторов в прямоугольной системе координат равно сумме произведений соответствующих координат, поэтому,

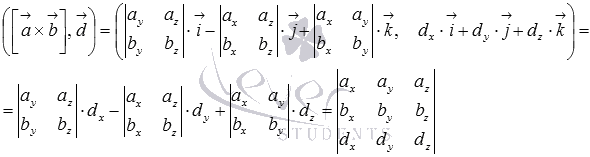
Таким образом, смешанное произведение векторов равно определителю матрицы третьего порядка, строками которой являются координаты умножаемых векторов, то есть,
.
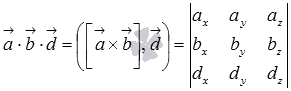