Способы реализации случайного механизма выбора стратегий

Для реализации применения игроком его активных стратегий с оптимальными вероятностями (относительными частотами), необходимо иметь случайный механизм выбора стратегий.

Например, если оптимальная смешанная стратегия 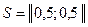(относительные частоты 1: 1), то для её реализации можно использовать подбрасывание монеты: если выпадает “герб”, применяется первая стратегия, а если “решка”, – вторая.

Игральную кость можно использовать при относительных частотах 1: 5; 2: 4; 1: 1; 4: 2; и так далее до 5: 1.

Секундная стрелка часов может служить для выбора случайных чисел от 0 до 59, если только игрок не смотрел на часы недавно и не знает наперед, даже приблизительно, ответ.

Но на практике могут потребоваться любые сочетания чисел в качестве относительных частот. Механизмом, удовлетворяющим вышеуказанному требованию, является датчик случайных чисел R от 0 до 1 с равномерной плотностью вероятности.

Так как стратегии A ₁, A ₂,..., A_m несовместны (в каждый момент применяется лишь одна из этих стратегий) и образуют полную группу событий , то для реализации случайного механизма выбора стратегий поступают следующим образом. Делят интервал (0, 1) на m участков длиной p ₁, p ₂,..., p_m (рис. 3.13). На какой из участков попало число R – ту стратегию и следует в данной партии использовать.

Рис. 3.13. Реализация случайного механизма выбора стратегий

Возникает вопрос: а как же реализуется сам датчик случайных чисел R? Самый простой из датчиков случайных чисел (ДСЧ) – это вращающийся барабан, в котором перемешиваются пронумерованные шары. Пусть, например, нам надо разыграть случайное число R от 0 до 1 с точностью 0, 001. Заложим в барабан 1000 пронумерованных шаров и после выбора случайным образом одного из шаров разделим его номер на 1000.

Можно поступить и иначе: вместо1000 шаров заложить только 10, с номерами 0, 1, 2,...., 9. Вынув случайным образом первый шар и разделив его номер на 10, получаем первый десятичный знак дроби. Вернём шар в барабан и опять приведём барабан во вращение. Выберем случайным образом второй шар, – его номер даст второй десятичный знак и т.д.

Можно доказать, что получаемые таким образом десятичные дроби будут иметь равномерное распределение от
0 до 1. Достоинство этого способа в том, что он может обеспечить любую точность задания числа R.

На практике широко применяются таблицы случайных чисел. Ниже приведен пример такой таблицы (рис.3.14). Числа сгруппированы лишь для удобства пользования таблицей. Можно начинать с любой точки таблицы, отсчитывать числа вверх или вниз, группировать числа.

Как использовать таблицу случайных чисел, чтобы получить желаемые относительные частоты? Возьмем в качестве примера оптимальную стратегию . Далее выбираем из таблицы любое случайное однозначное число. Если это число равно 0, 1, 2, 3 или 4, используем в данной партии первую стратегию. Если число равно 5 или 6, применяем вторую стратегию. Если это число равно 7, 8 или 9, то отбрасываем его и берём число под ним. Для следующей партии используется число ниже предыдущего.

Часто желательно модифицировать этот способ. Например, в случае относительных частот 8: 3 сумма чисел равна 8+3=11. Приходится применять двухзначные числа от 00 до 99. Но чтобы не отбрасывать числа от 11 до 99, разделим 99 на 11, получаем 9 (в общем случае это будет смешанная дробь). Далее умножаем 8× 9 = 72 и 3× 9 = 27. Теперь, если выбранное двухзначное число лежит в пределах от 00 до 71, используем первую стратегию, а если от 72 до 99, – вторую. Число 99 будем отбрасывать.

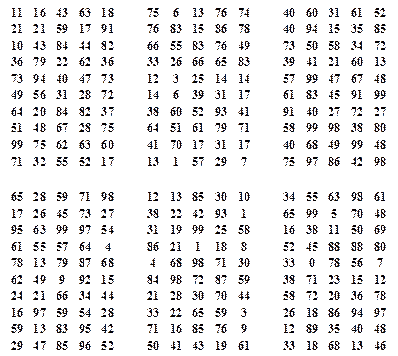
Рис.3.14. Таблица случайных чисел

Для получения R в ЭВМ применяются специальные датчики случайных чисел. Это могут быть как “физические датчики”, принцип действия которых основан на преобразовании случайных шумов, так и вычислительные алгоритмы, по которым сама машина вычисляет так называемые “псевдо­случайные” числа. Один из самых простых алгоритмов вычисления псевдослучайных чисел состоит в следующем. Берут два произвольных n -значных числа a ₁ и a ₂, перемножают их, и в полученном результате берут n средних знаков. Так получают число а ₃. Затем перемножают а ₂ и а ₃ и в полученном результате берут n средних знаков, получая число а ₄, и т.д. Полученные таким образом числа рассматриваются как последовательность двоичных дробей с n знаками после запятой. Такая последовательность дробей практически ведет себя как ряд случайных чисел R от 0 до 1.

В заключение изложения матричных игр отметим, что хотя само понятие смешанной стратегии требует многократного повторения партий игры, полученные результаты справедливы и к играм, которые играются только один раз, поскольку все изложения теории были выведены применительно к одной партии игры.

Качественно аргументировать этот тезис можно следующим образом: очевидно, что если противник узнает, какую мы выбрали стратегию, то предпримет ход, который будет иметь для нас наихудшие последствия. Поэтому единственным выходом является использование для выбора стратегии случайного механизма (жребия), результат которого противник не может предвидеть (хотя, конечно, ему может и повезти). Теория игр указывает на характеристики (частоты применения стратегий), которыми должен обладать используемый случайный механизм выбора стратегии в каждой партии.