Чистые и смешанные стратегии

Если в игре каждый из противников применяет только одну и ту же стратегию, то про саму игру в этом случае говорят, что она происходит в чистых стратегиях, а используемые игроком А и игроком В пара стратегий называются чистыми стратегиями.

Определение. В антагонистической игре пара стратегий (А_i, В_j) называется равновесной или устойчивой, если ни одному из игроков не выгодно отходить от своей стратегии.

Применять чистые стратегии имеет смысл тогда, когда игроки А и В располагают сведениями о действиях друг друга и достигнутых результатах. Если допустим, что хотя бы одна из сторон не знает о поведении противника, то идея равновесия нарушается, и игра ведется бессистемно.

В рассмотренном в 3.3.2 примере 1 максиминные чистые стратегии А ₄ и В ₅ неустойчивы по отношению к информации о поведении противника; они не обладают свойством равновесия.

Действительно, предположим, что мы узнали, что противник придерживается стратегии В ₃. Используя эту информацию, выберем стратегию А ₁ и получим больший выигрыш, равный 7. Но если противник узнал, что наша стратегия А ₁, он выберет стратегию В ₄, сведя наш выигрыш к 4.

Таким образом, в рассмотренном примере максиминные чистые стратегии оказались неустойчивы по отношению к информации о поведении другой стороны. Но это не всегда так.

Рассмотрим матричную игру G (3´ 4), платёжная матрица которой приведена на рис 3.4.

Рис. 3.4. Пример матричной игры с седловой точкой

В этом примере нижняя цена игры равна верхней:
a = b = 9 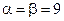, т.е. игра имеет седловую точку.

Оказывается, что в этом случае максиминные стратегии А ₂ и В ₂ будут устойчивыми по отношению к информации о поведении противника.

Действительно, пусть игрок А узнал, что противник применяет стратегию В ₂. Но и в этом случае игрок А будет по-прежнему придерживаться стратегии А ₂, потому что любое отступление от стратегии А ₂ только уменьшит выигрыш. Равным образом, информация, полученная игроком В, не заставит его отступить от своей стратегии В ₂.

Пара стратегий А ₂ и В ₂ обладает свойством устойчивости, а выигрыш (в рассматриваемом примере он равен 9), достигаемый при этой паре стратегий, оказывается седловой точкой платёжной матрицы.

Признак устойчивости (равновесности) пары стратегии – это равенство нижней и верхней цены игры.

Стратегии А_i и В_j (в рассматриваемом примере А ₂, В ₂), при котором выполняется равенство нижней и верхней цены игры, называются оптимальными чистыми стратегиями, а их совокупность – решением игры. Про саму игру в этом случае говорят, что она решается в чистых стратегиях.

Величина

(3.5)

называется ценой игры.

Если n > 0 , то игра выгодна для игрока А, если n < 0 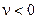– для игрока В; при n = 0 игра справедлива, т.е. является одинаково выгодной для обоих участников.

Однако наличие седловой точки в игре – это далеко не правило, скорее, – исключение. Большинство матричных игр не имеет седловой точки, а следовательно, не имеет оптимальных чистых стратегий. Разновидностью игр, которые всегда имеют седловую точку и, значит, решаются в чистых стратегиях, являются игры с полной информацией.

Теорема 2. Каждая игра с полной информацией имеет седловую точку, а следовательно, решается в чистых стратегиях, т.е. имеется пара оптимальных чистых стратегий, дающая устойчивый выигрыш, равный n.

Например, шахматная игра, как игра с полной информацией, либо всегда кончается выигрышем белых, либо всегда выигрышем черных, либо всегда ничьей (только чем именно – мы пока не знаем, так как число возможных стратегий в шахматной игре огромно).

Если матрица игры содержит седловую точку, то её решение сразу находится по принципу максимина.

Возникает вопрос: как найти решение игры, платёжная матрица которой не имеет седловой точки? Применение максиминного принципа каждым из игроков обеспечивает игроку А выигрыш не менее a, игроку В проигрыш не больше b. Учитывая, что 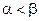, естественно для игрока А желание увеличить выигрыш, а для игрока В – уменьшить проигрыш. Поиск такого решения приводит к необходимости применять смешанные стратегии: чередовать чистые стратегии с какими-то частотами.

Определение. Случайная величина, значениями которой являются чистые стратегии игрока, называется его смешанной стратегией.

Таким образом, задание смешанной стратегии игрока состоит в указании тех вероятностей, с которыми выбираются его чистые стратегии.

Будем обозначать смешанные стратегии игроков А и В соответственно

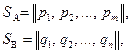
где p_i – вероятность применения игроком А чистой стратегии А_і; ;

q_j – вероятность применения игроком В чистой стратегии B_j; .

В частном случае, когда все вероятности, кроме одной, равны нулю, а эта одна – единице, смешанная стратегия превращается в чистую.

Применение смешанных стратегий осуществляется, например, таким образом: игра повторяется много раз, но в каждой партии игрок применяет различные чистые стратегии с относительными частотами их применения, равными p_i и q_j.

Смешанные стратегии в теории игр представляют собой модель изменчивой, гибкой тактики, когда ни один из игроков не знает, какую чистую стратегию выберет противник в данной партии.

Если игрок А применяет смешанную стратегию , а игрок В смешанную стратегию 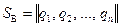, то средний выигрыш (математическое ожидание) игрока А определяется соотношением

. (3.6)

Естественно, что ожидаемый проигрыш игрока В равен такой же величине.

Итак, если матричная игра не имеет седловой точки, то игрок должен использовать оптимальную смешанную стратегию, которая обеспечит максимальный выигрыш n.

Возникает вопрос, какими соображениями нужно руководствоваться при выборе смешанных стратегий? Оказывается принцип максимина сохраняет свое значение и в этом случае. Кроме того, Важное значение для понимания решения игр играют основные теоремы теории игр.