Дискретно - стохастические модели

Дискректно - стохастические модели классифицируются как вероятностные автоматы, которые отличаются от конечных автоматов тем, что функции 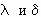представляют собой распределение вероятностей, т.е. при данном состоянии q(t) и данном входе x(t) следующие состояния случайны. При этом известны вероятности попадания в каждое из состояний:

Сказанное относится и к выходу. Вероятность осуществления события является условной и выполняется при условии, что имело место равенство Важным частным случаем является вероятностный автомат без входа и выхода. Такой автомат называется цепью Маркова. Цепь Маркова является частным случаем марковского случайного процесса с дискретным состоянием и дискретным временем.

Если известно начальное состояние, то в последующие моменты времени цепь проходит через свои состояния случайным образом. Поэтому в каждый момент времени t=n можно говорить о вероятности p 4i 0(n) того, что цепь находится в состоянии i, i=1, 2...m. Применение формулы полной вероятности дает соотношение

По этой формуле можно найти распределение вероятностей состояния для любого момента времени.

Основным моментов теории марковских цепей является теорема Маркова о стационарном режиме.