Гармонические функции

Связь с аналитическими функциями. Аналитические функции тесно связаны с гармоническими функциями от двух переменных, т. е. с решениями двумерного уравне­ния Лапласа

(1)

В самом деле, дифференцируя первое из условии ана­литичности

(2)

по x, а второе по у и приравнивая смешанные производные и 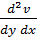, мы найдем, что функция u – действительная часть аналитической функции - является гармонической функцией. Точно так же доказывается, что и мнимая часть аналитической функции является функцией гармонической.

С другой стороны, для каждой гармонической в о д н о с в я з н о й области D функции и можно найти дру­гую гармоническую в D функцию v, которая называется сопряженной гармонической к и и вместе с которой и удовлетворяет системе (2), так что f будет аналитической в D. В самом деле, в силу уравнения (1) выражение в односвязной области является точным дифференциалом некоторой функции v, которая и является искомой. Таким образом, сопря­женные гармонические функции находятся простым ин­тегрированием.

Из свойств аналитических функций можно выводить соответствующие свойства функций гармонических (при желании можно поступать и наоборот). Так, мы можем утверждать, что каждая гармоническая функция беско­нечно дифференцируема. Из формулы (19) предыду­щего параграфа отделением действительных частей мы получаем теорему о среднем для гармонических функций:

(3)

Где r столь мало, что круг {|ζ — z|< r} принадлежит области гармоничности и.

Эта теорема является одним из основополагающих фактов теории гармонических функций. Из нее, в ча­стности, получается важный принцип экстремума: непо­стоянная гармоническая в области D функция не может достигать внутри D ни максимума, ни минимума.

Задача Дирихле. Принцип экстремума показывает, что гармоническая в области D и непрерывно продол­жающаяся в замыкание функция полностью опреде­ляется своими значениями па границе. Действительно, пусть существуют две такие функции u₁ и u₂ с одина­ковыми граничными значениями. Тогда их разность u₁ – u₂ будет гармонической в D и непрерывной в функцией, равной нулю всюду на границе. По свойствам непрерывных функций u₁ – u₂ должна достигать и мак­симума и минимума где-то в , а по принципу экстре­мума это должно происходить на границе. Но там u₁ — и₂ 0, следовательно, и максимум и минимум u₁ — и₂ в оба равны нулю. Таким образом, u₁ — и₂ 0, т. е. u₁ и₂ всюду в D.

Возникает естественная задача восстановления гар­монической в области функции по ее граничным значениям. Эта задача является основной в теории гар­монических функций и ее приложениях и называется задачей Дирихле. Вот как она формулируется:

На границе у области D задана функция и(ζ), тре­буется найти гармоническую в D и непрерывную в функцию u(z) так, чтобы в каждой точке ζ она принимала заданные значения и(ζ).

Приведенное выше рассуждение показывает, что за­дача Дирихле не может иметь двух различных реше­ний, т. е. доказывает единственность решения этой задачи. Более тонким и сложно доказываемым фактом является существование решения задачи Дирихле. Впрочем, для ряда простейших областей су­ществование решения можно доказать прямой кон­струкцией.

Пусть, например, D представляет собой единичный круг. Предположим сначала, что задача решена и мы нашли гармоническое продолжение и (z) заданной на окружности функции u(ζ). Тогда мы можем построить сопряженную с ней гармоническую функцию v (z) и к аналитической в круге функции f = и + iv применить интегральную формулу Коши:

(4)

Постараемся преобразовать правую часть этой фор­мулы так, чтобы ее действительная часть содержала лишь известные граничные значения и и не зависела от v. Для этого возьмем точку и, заметив, что она не принадлежит единичному кругу (ибо у нас и, следовательно , воспользуемся теоремой Коши, по которой

.

Теперь мы вычтем это равенство из предыдущего, пред­варительно подсчитав, что

(У нас ζ =|ζ |²= 1) и что при = 1 мы имеем ζ = мы получим

Наша цель достигнута, ибо справа при f (ζ) стоит действительный множитель. Отделяя формуле действительные части, мы получим так назы­ваемый интеграл Пуассона

u (z) = dt (z= (5)

Прямой оценкой можно доказать, что он и решает за­дачу Дирихле для круга - при любой непрерывной па окружности функции и(e^it) определяет гармоническую в круге функцию и (z) с заданными граничными зна­чениями.

Преобразованием формулы Коши (4), похожим на описанное, можно получить также интеграл Шварца который восстанавливает аналитическую в единичном круге функцию f(z) по граничным значениям ее дей­ствительной части:

(6)

эта задача, очевидно, решается с точностью до мнимой постоянной.

Такую же задачу для полосы {0 < у < 1} решает формула

} dt+iC, (7)

где и₀ и обозначают, соответственно, значения действительной части f на нижней и верхней границах по­лосы.

Связь с конформными отображениями. Между гар­моническими и аналитическими функциями имеется еще одна связь — гармоничность сохраняется при аналити­ческих преобразованиях. Это выражается следующей теоремой: если функция и(z) гармонична в области D, а функция () аналитична в области и принимает там значения из D, то сложная функция u[ ()] = U () гармонична в . Теорема доказывается пря­мым подсчетом, по которому оператор Лапласа

() = . (8)

В частности, гармоничность сохраняется при кон­формных отображениях, которые представляют собой взаимно однозначные аналитические преобразования.

Связь теории гармонических функций с теорией кон­формных отображений проявляется также в связи со­ответствующих граничных задач. Основной граничной задачей теории конформных отображении служит сле­дующая задача Римана:

Заданы две односвязные области D и 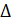; требуется построить функцию — f (z), реализующую конформ­ное отображение одной из этих областей на другую.

Эту задачу мы обсудим в следующей главе, а здесь лишь укажем ее связь с задачей Дирихле. Прежде всего, если для некоторой области D мы умеем решать задачу Римана и, следовательно, знаем ее конформное отображение f на единичный круг то мы можем решать для этой области и задачу Дирихле.

В самом деле, если граница области D является про­стой непрерывной кривой (что мы и предположим), то, как доказывается в теории конформных отображений, f продолжается до непрерывного и взаимно однозначного отображения на . Поэтому на единичной окружно­сти | |=1 мы можем рассматривать обратную к f функцию f ^--1 и с ее помощью перенести на эту окруж­ность заданные граничные значения: U( Теперь по этим значениям мы можем при помощи интеграла Пуассона построить гармоническую в круге | < 1 функцию

Остается вернуться к переменной z и воспользоваться сохранением гармоничности при конформных отображе­ниях; мы получим искомое решение:

u(z) = U [f(z)].

Во многих случаях оказывается полезным обратный ход — построение конформного отображения области D на единичный круг при помощи решения в D задачи Дирихле. Зададимся точкой z₀ D, которую искомое отображение f переводит в центр круга = 0 (рис. 19).

В ней функция f должна иметь нуль, и притом первого порядка, ибо в окрестности нулей высшего порядка аналитическая функция не взаимно однозначна (она имеет там характер степени). Поэтому в окрестности z₀ функция f должна иметь тейлоровское разложение вида

f (z) = c₁ (z — z₀) + с₂ (z — z₀)² +...,

где c₁=f’(z₀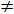₎ 0. Отсюда следует, что функция = c₁ + с₂ (z — z₀)² +..., аналитична в точке z₀, а в ос­тальных точках D она и подавно аналитична. Нигде в области D эта функция не обращается в 0, потому что числитель дроби равен 0 лишь при z = z₀, но там эта функция равна c₁ . Но тогда логарифм этой функции аналитичен в D, а значит, его действительная часть, т. е. функция

u(z) = log , (9)

должна быть гармонической в D.

Теперь уже нетрудно понять замысел проведенных построений, ведь если f отображает D на единичный круг, то | f (z)| должен равняться 1 на границе D а зна­чит, еще не зная самого конформного отображения, мы знаем граничные значения функции (9), они равны

u(ζ) = log , (10)

и определяются геометрической формой границы об­ласти и выбранной точкой z₀ (рис. 19). Чтобы найти ис­комое конформное отображение, нужно, следовательно, выполнить следующие операции: 1) по известным гра­ничным значениям (10) построить гармоническую в D

Рис. 20.

функцию u(z) (задача Дирихле), 2) найти функцию v(z), гармонически сопряженную с и (интегрирование). Теперь мы знаем функцию

g (z) = и (z) + iv (z) = log ,

откуда искомое отображение находится по формуле

f(z)=(z-z₀)e^g(z). (11)

Хочется обратить внимание на некоторые тонкости, связанные с построенным решением. Из конструкции видно, что функция f аналитична в D и что на грани­це D ее модуль равен 1. Однако остается еще доказать, что эта функция взаимно однозначно отображает D на единичный круг. Это можно сделать прямой (по отнюдь не простой) проверкой. Если же у нас есть уверенность, что наша задача разрешима (т. е. мы умеем доказывать теорему существования конформного отображения D на круг), то такая проверка излишня — проведенные выше рассуждения показывают, что если искомое отображе­ние есть, то оно непременно восстанавливается по фор­муле (И).

В заключение заметим, что задача конформного ото­бражения криволинейной полосы D = {у₀(х) < у < < y(х)} на прямолинейную полосу = {0 < v < h} с нормировкой f (± ) = + сводится к задаче Ди­рихле еще проще. Из геометрических соображений (рис. 20) ясно, что гармоническая функция v = 1m f на нижней границе Г₀ полосы D должна принимать значе­ние v 0, а на верхней границе Г — значение v , кроме того, функция v должна быть ограниченной (О ). Таким образом, искомую гармоническую функцию и мы знаем па всей границе области D исклю­чая бесконечные точки х = ± . Можно доказать, что эта обобщенная задача Дирихле имеет и притом един­ственное решение v в классе ограниченных гармониче­ских функций. Интегрированием мы найдем сопряжен­ную гармоническую к v функцию и (с точностью до постоянного слагаемого) и тогда f = и + iv будет ис­комым конформным отображением.

Г л а в а IX
ВИХРИ

В этой главе изложены некоторые результаты тео­ретических и экспериментальных исследований, связан­ных с образованием, структурой и движением кольце­вых вихрей.

Несмотря на большое число работ, посвященных этой проблеме, многие важные и интересные вопросы, к ней относящиеся, до последнего времени оставались без ответа. Исследования, проведенные за последнее де­сятилетие, улучшили положение. Были поставлены мно­гочисленные опыты, на основе которых создана мате­матическая модель, позволяющая определить закон движения, структуру кольцевых вихрей, количество при­меси, которое они могут переносить, и другие характе­ристики. Полученные результаты дают хорошее совпа­дение с опытом.

Более трудным для исследования оказался механизм образования кольцевых вихрей. Здесь получены неко­торые экспериментальные результаты, дающие основу для качественного понимания явления, однако задача его полного математического описания еще не решена.