Кольцевые вихри

Если обычному воздушному шарику в резиновой обо­лочке сообщить скорость 5—10 м/сек, то он проходит расстояние 1, 5 2 м. С другой стороны, давно известно, что если с той же скоростью кинуть (например, вытолк­нуть поршнем из трубки) такую же массу воздуха без оболочки, то она пройдет расстояние, в 10—15 раз большее.

Опыт показывает, что во втором случае движение происходит так, как показано на рис.121, где изобра­жены линии тока для движения относительно системы координат, движущейся вместе с вытолкнутой массой воздуха. Движение обладает осевой симметрией; внутри выпуклой области, образованной вращением участка АВС линии тока, оно вихревое, а вне этой области – практически потенциальное. На АВС скорости внутрен­него и внешнего движений совпадают, так что поле скоростей оказывается непрерывным. Это и объясняет эффект, с которого мы начали, – из-за непрерывности трение на границе, движущейся без оболочки массы меньше, чем массы в оболочке, следовательно, мень­ше сопротивление и больше про­ходимое массой расстояние.

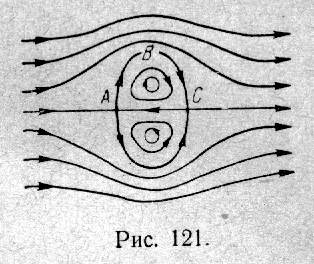
Аналогичное движение мож­но наблюдать и в воде. Оно из­вестно уже давно и называется кольцевым вихрем. В конце прошлого века такая схема движения привлекала внимание в связи с попытками создания вихревой модели атомов (У. Томсон-Кельвин, Дж. Дж. Томсон). Эти попытки успеха не имели, но они послужили поводом для интересных исследований, с ко­торыми можно ознакомиться по книге Ламба [4].

Интерес к проблеме сильно возрос после появления атомных бомб, при взрыве которых образуется харак­терное грибовидное облако, структура которого анало­гична структуре кольцевого вихря, изображенного на фото рис. 122. Такое облако с большой скоростью под­нимается на высоту нескольких километров. Аналогич­ное явление наблюдается и при взрыве больших заря­дов обычных ВВ.

В последнее время исследуются возможности прак­тического применения кольцевых вихрей для удаления дыма, вредных газов и т. п. на промышленных пред­приятиях. В связи с этим возникает много вопросов, от­веты на которые нельзя получить без учета вязкости, диссипации энергии, турбулентного характера движения и т. д. Однако прежде чем переходить к описанию ма­тематической модели, учитывающей эти факторы, мы должны напомнить некоторые результаты, полученные в схеме идеальной несжимаемой жидкости.

Вихри в идеальной жидкости. Если пренебречь вяз­костью и рассматривать осесимметричные движения не­сжимаемой жидкости, стационарные в системе

коорди­нат, движущейся вместе с вихрем, то уравнения, связывающие функцию тока 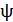и завихренность 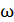в цилинд­рических координатах (r, ɑ, z), имеют вид

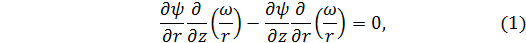
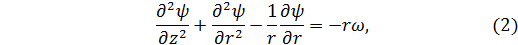
(см. гл. I). Из (1) следует, что отношение постоянно вдоль линии тока, т. е. что

где F – произвольная функция.

Так как движение на бесконечности должно быть потенциальным, то F должна тождественно обращаться в нуль вне некоторой области, ограниченной замкнутой линией тока, а на этой линии составляющие скорости должны быть непрерывными. При заданной F возникает типичная задача о склейке потенциального и вихревого течения, аналогичная тем, кторые мы рассматривали в гл. V.

В такой форме эта задача не исследована даже для простейших функций F, известны только отдельные при­меры точных и приближенных решений. Пример точногo решения дает сферический вихрь Хилла. Здесь завихрен­ность распределена внутри шара радиуса по закону

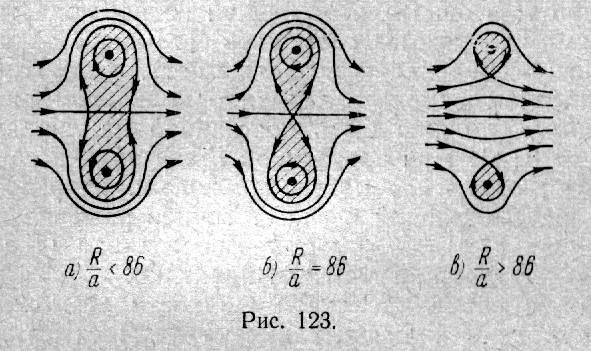
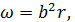где b –постоянная; вне шара поток – потен­циальный и жидкость, содержащаяся в этом шаре, движется вместе с вихрем со скоростью

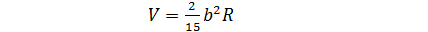(4)

относительно неподвижной системы координат (см. Л а м б [4], стр. 309—310).

Вихри такого типа в опытах не наблюдаются. Боль­шее сходство с наблюдениями имеет приближенное ре­шение, полученное еще Максвеллом, где завихренная область представляет собой тор, радиус а поперечного сечения которого много меньше радиуса R самого тора. Тороидальный вихрь Максвелла движется со скоростью

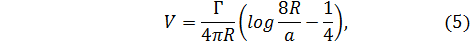
а форма объема, заключенного внутри замкнутой по­верхности тока и движущегося вместе с вихрем, зависит от отношения 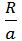(см. Лам б [4], стр. 299—305). На рис. 123 изображены линии тока при различных 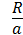; область, движущаяся вместе с вихрем, на этом рисунке заштрихована, а область завихренной жидкости зачернена. При < 86 форма области, движущейся с вих­рем, мало отличается от наблюдаемой. При > 86 эта область, как и область завихренности, имеет тороидаль­ную форму; в опытах этот случай не наблюдается, что, по-видимому, можно объяснить его неустойчивостью (строгого исследования здесь еще нет).

В плоском варианте задачи о кольцевом вихре за­вихренность должна быть постоянной на линиях тока, т. е. 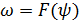. При постоянной F эта задача совпадает с задачей о склейке потенциального и вихревого дви­жения, рассмотренной в гл. V. Точное решение имеется для случая 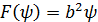, где b – постоянная (Л а м б [4], стр. 308—309), но он далек от практики.

Итак, в схеме идеальной жидкости возможны раз­личные модели кольцевых вихрей — эта схема не дает никаких условий для определения вида функции F и формы области, в которой завихренность отлична от нуля. Поэтому ясно, что решения, полученные в рамках невязкой несжимаемой жидкости, не позволяют опреде­лить изменение скорости и размеров вихрей, наблюдае­мых в экспериментах.

Влияние вязкости. Вязкость жидкости приводит к диссипации энергии, поэтому движение вихря в отсут­ствии внешних сил становится нестационарным. Можно было бы ожидать, что закон движения и распределение завихренности в кольцевом вихре определяются началь­ными и краевыми условиями и, следовательно, суще­ственно зависят от способа образования вихря. Однако опыт показывает, что дело обстоит не совсем так.

Классический способ образования вихря состоит в следующем: в верхней крышке коробки с эластичным дном делается отверстие, диаметр которого существенно меньше, чем размеры коробки. К отверстию могут при­крепляться насадки в виде сопел различной формы. Ко­робка наполняется дымом, после чего по дну произ­водится удар.

При малых числах Рейнольдса, определяемых радиу­сом и скоростью вихря, образуется ламинарный вихрь с четко выраженной спиральной структурой, хорошо ви­димой на фотографиях¹) (рис. 124, а).

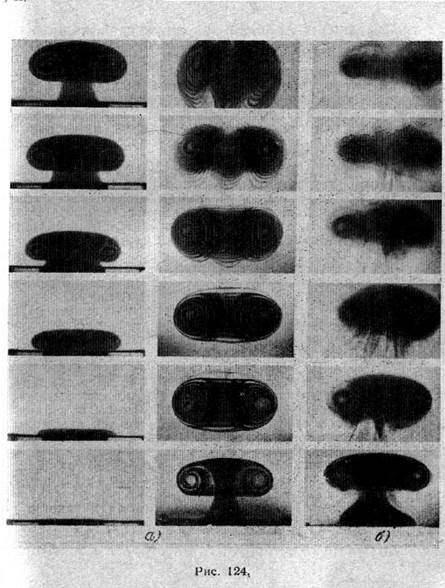
В этом случае распределение завихренности действительно опреде­ляется начальным полем скоростей, формой насадки, зависит от того, плавный или резкий был удар, и т. д. Это движение в принципе может быть описано с по­мощью уравнений Навье — Стокса, но решение соответ­ствующей нестационарной задачи, даже с применением вычислительных машин, связано с огромными трудно­стями.

С другой стороны, начиная с Rе ~ 10³, характер дви­жения резко меняется, оно становится турбулентным (рис. 124, 6). В этом случае, как показывает опыт, структура кольцевого вихря не зависит (или, по край­ней мере, зависит очень слабо) от деталей начальных и краевых условий. После того, как вихрь проходит рас­стояние порядка нескольких радиусов отверстия, вырабатывается некоторое распределение завихренности, вообще не зависящее от способа образования вихря. Усредненное движение в турбулентном вихре опреде­ляется только размером и скоростью вихря. При дальнейшем движении, как показывает эксперимент, размеры вихря линейно увеличиваются с пройденным расстоянием, причем форма вихря преобразуется подобно.

Турбулентная вязкость. Турбулентное движение вяз­кой жидкости, как известно, не описывается замкнутой системой уравнений – в каждом конкретном случае для получения такой системы приходится выдвигать допол­нительные гипотезы, т. е. рассматривать какую-либо модель движения.

В безграничном пространстве турбулентно движу­щуюся жидкость можно описывать как жидкость, обладающую некоторой, как говорят, турбулентной вязкостью , отличной от истинной кинематической вяз­кости. Такое феноменологическое описание свободной турбулентности (в отсутствии границ) дает хорошие результаты в теории турбулентных струй и в некоторых других случаях.

Турбулентный характер движения жидкости в коль­цевом вихре можно описать введением коэффициента турбулентной вязкости 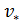. Предположим, что этот коэф­фициент есть некоторая функция времени, не зависит от пространственных координат и определяется харак­терными масштабами движения (размером и скоростью вихря). Более того, предположим, что

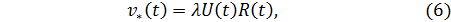
где U и R — скорость и радиус вихря ¹), а коэффициент 𝞴 постоянная, величина которой должна определяться сравнением результатов расчета с экспериментом.

Опыт показывает, что на значительном участке дви­жения вихря турбулентная вязкость во много раз боль­ше кинематической, и последней можно пренебречь Окончательно получаем следующее: усредненное движе­ние турбулентного вихря описывается уравнениями Гельмгольца (гл. I), в которые вместо кинематической вязкости входит турбулентная вязкость .

Уравнения Гельмгольца. Будем рассматривать в вяз­кой жидкости одновременно осесимметричные кольце­вые вихри и соответствующий плоский аналог. В силу сделанных предположений система уравнений, описы­вающая такие движения, имеет вид:

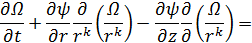
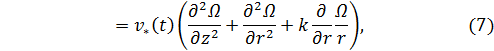
Уравнения (7) называются уравнениями Гельмгольца, при k =1 они описывают осесимметричное движение, а при k = 0 — плоское (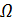 – соответствующая компо­нента вектора завихренности, функция тока).

Предположение о коэффициенте турбулентной вязко­сти заведомо неверно на больших расстояниях от коль­цевого вихря, так как там этот коэффициент должен обращаться в нуль. Однако из уравнений Гельмгольца (7) видно, что члены с вязкостью существенны только там, где завихренность заметно отличается от нуля. Посколь­ку в кольцевом вихре завихренность очень быстро уменьшается с удалением от него, можно ожидать, что сделанное предположение не будет давать существен­ной ошибки. Аналогичная ситуация имеет место в тео­рии турбулентных струй, дающей хорошее соответствие с экспериментом.

Система (7) обладает важным законом сохра­нения. Умножая первое уравнение на 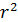при k = 1 или на 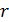при 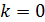и интегрируя по всему пространству, в предположении, что 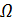и ее производные достаточно быстро стремятся к нулю на бесконечности, получим:

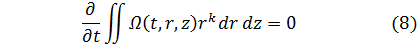
Этот результат есть частный случай общего утвержде­ния о том, что в безграничной вязкой жидкости, покоя­щейся на бесконечности, величина

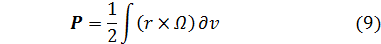
не зависит от времени (доказательство дано в работе [6]). Величину Р естественно назвать импульсом вихря, а постоянство этой величины есть не что иное, как за­кон сохранения импульса.

Автомодельная задача. Для полученной системы уравнений необходимо, вообще говоря, задать начальное условие – начальное распределение завихренности, опре­деляемое способом образования кольцевого вихря. Од­нако, как уже отмечалось раньше, распределение за­вихренности очень быстро приближается к некоторому распределению, не зависящему от начальных условий, которое в дальнейшем линейно зависит от расстояния. Естественно поэтому предположить, что предельное рас­пределение завихренности описывается автомодельным решением системы Гельмгольца (4).

Поставим следующую задачу, которую снова будем рассматривать и в осесимметричном и в плоском ва­риантах. Пусть в момент времени t = 0 завихренность 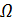равна нулю всюду в безграничном пространстве, за исключением начала координат, где в осесимметричном случае расположен кольцевой вихрь бесконечно малогo радиуса и бесконечной большой интенсивности так, что

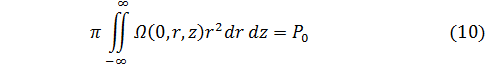
В плоском варианте будем считать, что в начале коор­динат имеется вихревой диполь: пара вихрей бесконечно большой интенсивности и противоположных знаков, рас­положенных на бесконечно малом расстоянии друг от друга так, что

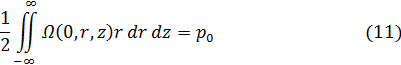
Легко видеть, что Р₀ и 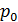– это импульсы кольцевого вихря в начальный момент соответственно для осесимметричного и плоского вариантов.

В такой постановке единственной размерной постоянной, определяющей движения вихря, будет 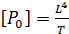в осесимметричном случае и 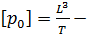в плоском. Следовательно, в осесимметричном случае искомые функци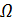и и 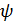имеют такой вид:

а турбулентная вязкость в соответствии с (6) – вид

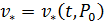
Анализ размерностей (см. § 4) позволяет уточнить вид этих функций, именно

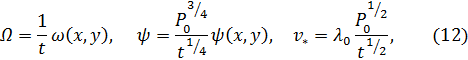
где

а 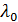— постоянная. Таким образом, сформулированная задача оказывается автомодельной (см. гл. I).

В плоском случае точно так же можно заключить, что искомые функции имеют следующий вид:

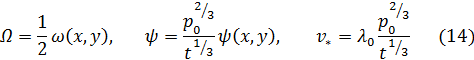
где

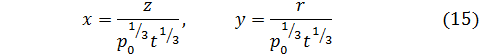
Подставляя выражения (12) и (14) в (7), мы полу­чим уравнения для определения и Ограничимся далее плоским случаем (k = 0); здесь получается сле­дующая система уравнений с частными производными:

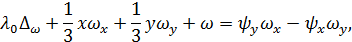
Нам нужно найти решения этой системы и 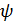, стре­мящиеся к нулю на бесконечности и удовлетворяющие условию нормировки

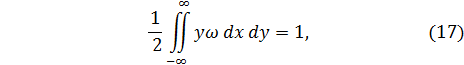
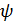которое следует из закона сохранения импульса и на­чального условия. Из соображений симметрии ясно так­же, что и должны быть нечетными функциями от у:

Постоянная 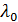, входящая в первое уравнение (16), остается неопределенной — ее величина должна опреде­ляться сравнением с экспериментом.

К сожалению, точное решение системы (16) получить не удается и мы ограничимся замечаниями общего ха­рактера. Назовем радиусом вихря и расстоянием, им пройденным, соответственно такие значения r = R(t) и z = L(t), при которых функция имеет макси­мум при фиксированном значении t. Эти величины, оче­видно, определяются равенствами, которые в осесиммет­ричном случае имеют вид

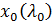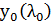здесь и – координаты точки, где достигает максимума функция 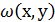, положение этой точки зави­сит от .

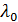Равенства (19) определяют закон движения вихря. Из них сразу следует, что

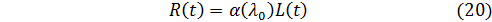
где

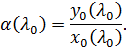
Мы получаем, что радиус вихря ли­нейно зависит от расстояния, им проходимого; этот ре­зультат хорошо подтверждается экспериментом. Вели­чина 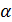измеряется в эксперименте и оказывается малой порядка 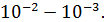Зная 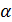и имея решение системы (16), можно определить .

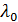Естественно ожидать, что малым 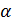соответствуют малые 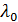, и следовательно, для сравнения с эксперимен­том достаточно получить решение системы (16) для ма­лых значений 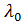. Но и эта задача оказалась сложной.

Модельная задача. Следуя Б. А. Л у г о в ц о в у [7], рассмотрим модельную задачу, в которой (16) заме­няется похожей системой уравнений

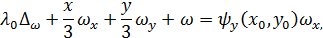
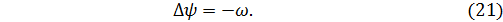
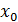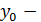где и координаты точки максимума функции (х, у).

Сделаем замену переменных, полагая

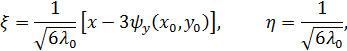
Тогда из первого уравнения (21) мы получим для 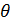уравнение

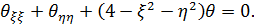
Оно допускает разделение переменных: полагая 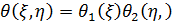мы сведем его к обыкновенным дифференциальным уравнениям

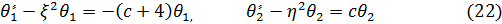
где с – постоянная разделения. Нас интересуют реше­ния, стремящиеся к нулю пр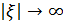и и кроме того, в силу (18) функция 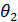должна быть нечетной.

Эта задача хорошо изучена – в квантовой механике ей соответствует задача о гармоническом осцилляторе (см. А. Н. Тихонов, А. А. Самарский [1]). Реше­ния уравнений (22), удовлетворяющие нашим дополни­тельным условиям, существуют только при

Отсюда следует, что л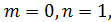ибо либо , а условие нечетности по 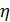оставляет только одну возможность 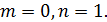Соответствующе решение имеет вид 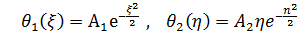, откуда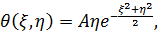

где А – произвольная постоянная, определяемая нормировкой (17).

Во втором уравнении (21) теперь правая часть из­вестна, и оно становится уравнением Пуассона, решение которого, обращающееся в нуль на бесконечности, опре­деляется формулой

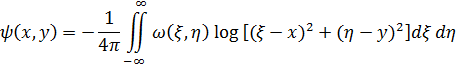
(см., например, В. С. Владимиров [2]).

Зная 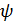, мы можем определить постоянную 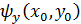и найти окончательное решение модельной задачи:

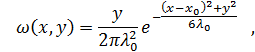
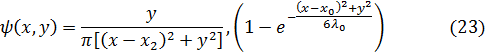
здесь координаты точки максимума

Следовательно,

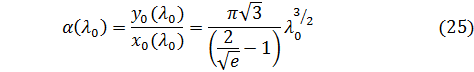
Это модельное решение можно использовать для грубой оценки положения максимума (х, у) в точной задаче, что очень важно для возможности применения числен­ных методов.

Сравнение с экпериментом. Закон движения вихря (19) дает хорошее согласие с экспериментом. Удобно преобразовать формулы (19) так, чтобы в них входили экспериментально изме­ряемые величины – началь­ный радиус 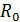и начальная скорость . В качестве на­чала отсчета удобно выби­рать не момент выхода вих­ря из отверстия, а более поздний момент, когда вихрь от отверстия отойдет на некоторое расстояние (че­тыре-пять диаметров отвер­стия), – это объясняется тем, что на вырабатывание автомодельного распределения завихренности в вихре необходимо некоторое время. Если время t и расстояние L(t), проходимое вихрем, от­считывать от этой точки, то вместо (19) получим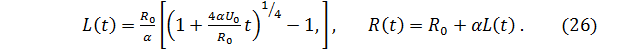

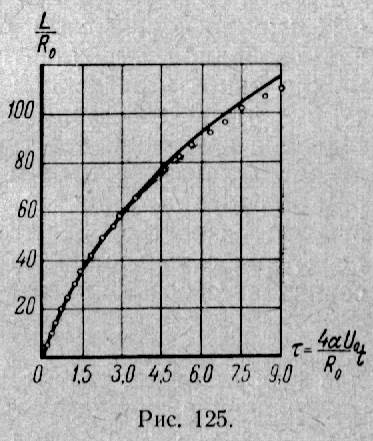
На рис. 125 кружками отмечены экспериментальные точки, соответствующие движению вихря, начальные па­раметры которого равны R₀ =10 см, = 4, 3 м/сек, а величина 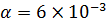. Сплошная кривая получена по формуле (26). Отклонение расчетной кривой от экспе­риментальных точек при больших t объясняется тем, что турбулентная вязкость со временем уменьшается и, на­чиная с некоторого момента, делается сравнимой с ки­нематической, после чего пренебрежение кинематической вязкостью становится неправомерным. После того как кинематическая вязкость становится существенной, вихрь быстро останавливается.