Перенос примесей

Турбулентная диффузия. Аналогичным образом мож­но изучить задачу о переносе турбулентным вихрем пас­сивной примеси, т. е. примеси, которая не оказывает влияния на его движение. Турбулентное перемешивание жидкости сопровождается переносом примесей в моляр­ных (макроскопических) объемах. Этот процесс в слу­чае свободной турбулентности (в отсутствии границ) можно описать введением специального «коэффициента турбулентной диффузии» 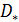, величина которого, как и величина коэффициента турбулентной вязкости , опре­деляется характерными масштабами движения (разме­ром и скоростью вихря). Из опытов с турбулентными струями известно [5], что коэффициент турбулентной диффузии с точностью до множителя порядка единицы совпадает с коэффициентом турбулентной вязкости:

для турбулентных струй

Уравнение, описывающее распределение примеси, концентрацию которой мы обозначим через С, имеет вид:

где D — молекулярный коэффициент диффузии (см. [5]).

Ясно, что на начальном участке движения вихря мо­лекулярным коэффициентом диффузии D можно прене­бречь по сравнению с турбулентным. Скорость V извест­на, если известно движение вихря.

Для уравнения (2) необходимо, вообще говоря, за­дать начальные условия, которые сводятся к заданию начального распределения концентрации, зависящего от способа заполнения вихря примесями. Эксперимент, од­нако, показывает, что так же, как и распределение завихренности, распределение концентрации примесей очень быстро приближается к некоторому распределению, не зависящему от начальных условий. При этом избыточные по отношению к предельному распределению количества примесей быстро теряются, а после этого потери примесей практически отсутствуют.

Автомодельная задача. Естественно предположить, что предельное распределение концентрации примесей является автомодельным [7]. Поставим следующую за­дачу (ограничиваясь плоским случаем). Пусть в момент времени концентрация С равна нулю всюду, кро­ме начала координат, где она бесконечно велика, так что

где — полное количество примеси (например, полное число частиц дыма). В этой же точке при нахо­дится и вихревой диполь с импульсом .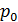

Ясно, что концентрация

а согласно (1) коэффициент турбулентной диффузии

так как по предположению примесь не оказывает влия­ния на движение жидкости.

В силу линейности уравнения (2) и нормировки (3) ясно, что С пропорциональна , и из анализа размер­ностей следует, что функции (4) и (5) имеют вид

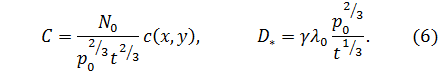
Подставляя это в (2), получаем уравнение для с

причем нас интересуют его решения, стремящиеся к нулю при и удовлетворяющие условию нормировки

Интересно отметить, что эта мощность не зависит от поперечных размеров обтекаемого тела (конечно, если форма этого тела получается описанным выше спосо­бом). Можно убедиться в том, что обтекание тела по рассмотренной схеме требует значительно меньшей мощ­ности, чем та, которая, например, затрачивается на об­текание плоской пластины сравнимых размеров (см.[3]).

Проделанный расчет справедлив для ламинарных течений. В действительности же, при достаточно боль­ших числах Рейнольдса, движение будет турбулентным, и необходимая мощность С} может увеличиться. Для вы­яснения фактической возможности снижения сопротив­ления за счет применения описанной схемы обтекания необходимы дальнейшие исследования.

Литература

1. А. Н. Тихонов и А. А. Самарски й, Уравнения математиче­ской физики, «Наука», М., 1966.

2. В. С. Владимиров, Уравнения математической физики, изд. 2-е, «Наука», М., 1971.

3. 3 Л. Д. Ландау и Е. М. Л и ф ш и и, Механика сплошных сред, ГИТТЛ, М, 1954.

4. Г. Л а м б, Гидродинамика. ГИТТЛ, М. — Л., 1947.

5. Л. А. Вулис, В. П. Каш кар о в, Теория струй вязкой жидко­сти, «Наука», М., 1965.

6. А. А. Л у г о в ц о в, Б. А. Л у г о в ц о в, В. Ф. Тарасов, О дви­жении турбулентного вихревого кольца, В сб «Динамика сплош­ной среды», вып. III, Новосибирск, 1969.

7. Б. А. Л у г о в ц о в, О движении турбулентного вихревого кольца и переносе им пассивной примеси, В сб. «Некоторые проблемы ма­тематики и механики» (к семидесятилетию М. А. Лаврентьева), «Наука», Л., 1970.

8. А. Т. Онуфриев, Теория движения кольца под действием силы тяжести. Подъем облака атомного взрыва, ПМТФ, 2 (1967).

9. А. А. Л у г о в ц о в, Б. А. Л у г о в ц о в, Пример обтекания тела с движущейся границей, В сб. «Динамика сплошной среды», вып.

УШ, Новосибирск, 1971.

§ 38. Неустойчивость стержней Статическая и динамическая потери устойчивости.

Простейший эксперимент, поясняющий различие между этими двумя формами потери устойчивости стержней, можно поставить так. Пусть стержень (т. е. упругая тонкая полоса) расположен вертикально, его нижний конец закреплен в твердом основании, а сверху на него действует не слишком большая вертикальная сила F(рис. 135). Если стержень немного отклонить от верти­кального положения и затем отпустить, то он будет совершать затухающие коле­бания вокруг положения равновесия и через некоторое время вернется в это положение. Мы имеем случай устойчиво­го равновесия.

Будем теперь постепенно увеличивать силу F. С ростом F частота колебаний уменьшается, и при некотором значе­нии F = F_кр частота обратится в нуль — стержень будет находиться в состоя­нии безразличного равновесия. При дальнейшем увеличении силы F равно­весие становится неустойчивым: после любых отклонений стержень изгибается и не возвращается в вертикальное поло­жение

Величина критической силы F_кр, при которой равно­весие перестает быть устойчивым, зависит от формы, размеров и упругих свойств стержня, а также от усло­вий его закрепления (граничных условий). Описанный выше процесс потери устойчивости, при котором вели­чина нагрузки постепенно увеличивается до тех пор, пока она не достигнет критического значения, называется статической потерей устойчивости.

Иначе ставится эксперимент по динамической потере устойчивости. Здесь в некоторый момент времени стер­жень немного изгибается, и к нему сразу приклады­вается вертикальная сила, величина которой превышает критическую. Оказывается, что в этой постановке по­теря устойчивости происходит иначе, чем при статиче­ском нагружении. Ниже мы рассмотрим это различие подробнее.

В механике упругих тел большинство изученных за­дач относится к случаю статической устойчивости. Наи­более классическая из таких задач была решена Л. Эйлером еще в 1744 году.

Задача Эйлера. Пусть концы стержня закреплены шарнирно, причем нижний шарнир неподвижен, а верх­ний может перемещаться вертикально; к верхнему концу прикладывается вертикаль­ная сила F (рис. 136). Предположим, что сечения стержня одинаковы, длина его рав­на l, момент инерции J и модуль Юнга Е.

При равновесии в каждом сечении стержня изгибающий момент упругих сил должен равняться моменту силы F отно­сительно середины изогнутого стержня. Мо­мент упругих сил, как известно, пропорцио­нален кривизне стержня k(х) в рассматри­ваемом сечении и равен ± EJk, а момент силы F в этом сечении равен ± Fу.

Задачу будем решать в линейном приближении, предполагая, что прогибы стержня малы. Тогда кривизна , и мы полу­чаем уравнение равновесия в виде

(знак выбран с учетом того, что у" > 0 при «y< 0 и наоборот).

Общее решение уравнения (1) имеет вид

где A и В — произвольные постоянные, а

Условие шарнирного закрепления концов приводит к граничным условиям

(4)

из которых следует, что В = 0 и

Если F < , то из (5) следует что A = 0, т.е. при этом условии возможно лишь тривиальное решение Если же F , то при условии , которое переписывается в виде

(п — произвольное целое число), кроме тривиального, возможны еще решения вида

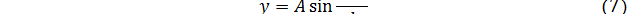
Мы получаем спектр собственных значений (6) вели­чины F, каждому из которых соответствует искривлен­ная равновесная форма стержня (7). Критической силой естественно считать ту, при которой перестает быть ус­тойчивой первоначальная прямолинейная форма стерж­ня. Очевидно, эта сила соответствует значению п=1 и равна

она называется эйлеровой силой. При медленном возра­стании нагрузки F потеря устойчивости происходит при этом значении . Стержень при этом изогнется в форме одной полуволны синусоиды, и если произойдет излом, то стержень распадется на два куска.

Отметим, что величина А амплитуды прогиба стерж­ня в приведенном выше решении задачи Эйлера никак не определяется и теоретически может быть сколь угод­но большой. Этот противоречащий действительности вывод является следствием линеаризации задачи. На самом деле при больших прогибах перестает быть обо­снованным приближенное выражение для кривизны, ко­торым мы пользовались при выводе уравнения (1). В этом случае надо использовать точное выражение , и задача становится нелинейной. Исследование устойчивости в нелинейной постановке также возможно, оно дает и конкретные результаты, но основ­ные выводы остаются примерно теми же, что и в линейной постановке. На конгрессе механиков в Калифорнии (1968 г.) этим проблемам был посвящен обзорный доклад французского ученого Л. Готье).

Динамическая постановка. При изучении действия взрыва на стержни и оболочки были обнаружены формы потери устойчивости, которые не укладываются в разобранную статическую схему.Представим себе следующий эксперимент.

Пусть имеется стержень, расположенный вертикаль­но и закрепленный так же, как в предыдущей задаче. Мы предположим, что разрушение стержня наступает при малых деформациях, когда еще применима линей­ная теория. Пусть сверху к стержню мгновенно при­лагается вертикальная сила F величина которой в не­сколько раз превышает Эйлерову силу . Нужно выяснить, как будет происходить потеря устойчивости стержня и его разрушение.

Как мы видели выше, в схеме статического нагру­жения стержень разламывается на два куска. Опыт по­казывает, что в принятых здесь условиях стержень раз­ламывается на несколько кусков, число которых зависит от отношения . Нашей задачей является выяснение движения стержня в начальный отрезок времени и опре­деление числа кусков, па которые он разламывается.

Как известно, уравнение малых движений стержня описывается дифференциальным уравнением

(9)

где — плотность материала и S — площадь попереч­ного сечения стержня; функция f определяется началь­ным искривлением, поперечной нагрузкой и т. п.

Решение этого уравнения, удовлетворяющее гранич­ным условиям (4), к которым теперь следует добавить у" =0 при х=0, l (в статической схеме эти условия выполнялись автоматически), естественно искать в виде ряда Фурье по синусам:

Если правая часть уравнения (9) также представлена рядом Фурье , то при подстановке (10) в это уравнение мы получим систему обыкновен­ных уравнений

где

Величина q_k представляет собой амплитуду той гармо­ники

которой соответствует изгиб стержня по синусоиде с k полуволнами.

Уравнение (11) показывает, что при закон изменения - синусоидальный, поэтому соответ­ствующие гармоники 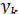имеют ограниченную ампли­туду и не дают потери устойчивости. При , на­против, решения уравнения (11) имеют непериодиче­ский характер:

где

(мы считаем, что 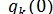= 0 (0) == 0). С течением вре­мени амплитуды соответствующих гармоник неограни­ченно возрастают, причем быстрее всего возрастает амплитуда той гармоники, для которой величина — наибольшая. Из (15) видно, что максимум дости­гается при , так что наибольшую неустойчи­вость дает синусоидальная форма стержня с числом по­луволн, равным ближайшему целому k числу

Естественно ожидать, что если стержень не выдер­жит нагрузки и сломается, то число изломов будет равно именно этому числу.

К тому же выводу можно прийти и из энергетиче­ских соображений. Существует принцип, согласно кото­рому движение консервативной механической системы осуществляется так, чтобы в каждый данный момент ее полная потенциальная энергия была возможно меньшей. (Скажем, в примере, которым начиналась глава, шарик скатывается по желобку на сферической поверхности, если такой желобок есть.)

Подсчитаем полную потенциальную энергию стержня в нашей задаче. Она составляется из энергии упругого изгиба стержня

П₁=

и потенциала внешних сил П₂ (продольным сжатием стержня и его начальным изгибом мы пренебрегаем). Потенциал П₂ равен работе силы F с противоположным знаком: П₂ = —F l, где l — смещение верхнего конца стержня по вертикали. Предполагая стержень нерастя­жимым и обозначая через l ₀ его длину, а через l — проекцию его верхнего конца на ось х, будем иметь

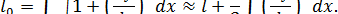
Так как = l₀ — l, то мы получим

П₂=

а значит,

П = П₁ + П₂ = 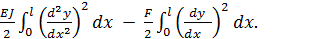(17)

Отсюда с учетом формул (12) получаем выражение полной потенциальной енергии для гармоники (13):

П = (18)

Мы видим, что минимальное значение П достигается для той гармоники у_k, номер которой равен ближай­шему целому к числу (16), т. е. той самой гармонике, которая дает наибольшую неустойчивость.

Таким образом, мы двумя способами пришли к од­ному и тому же выводу: когда к стержню мгновенно прикладывается нагрузка F в п раз превышающая кри­тическую эйлерову силу F_кр, то стержень изгибается

по синусоиде с числом полуволи, равным или ближайшему целому числу; если стержень при этом разрушается, то число изломов также оказывается равным

этом числу.

На рис. 137 приведены фотографии эксперимента, иллюстрирующего изгиб стержня при динамической нагрузке и его разрушение на несколько кусков ¹). Ко­нечно, на практике наш вывод осуществляется лишь в вероятностном смысле: при проведении большого числа опытов среднее число осколков близко к .

Интересно отметить, что аналогичный результат наблюдается при мгновенном нагружении тонкостенной рубки, когда эта трубка подвергается внешнему давле­нию. Так же, как в случае стержня, имеется критиче­ское давление F_кр такое, что если внешнее давление на трубку меньше критического, то трубка ус­тойчива; если сжать ее в пределах упруго­сти, то при снятии сжимающей силы она вернется в прежнее состояние. Если же дав­ление превысит критическое, то трубка по­теряет устойчивость в прежнем смысле.

Если нагрузка будет в п раз больше крити­ческой, то мы получим деформацию с коли­чеством волн порядка .

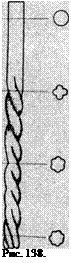
Наиболее яркий пример динамической неустойчивости дает следующий опыт. Если тонкостенную трубку с заделанными кон­цами погрузить в воду, а затем вблизи нижнего конца произвести взрыв, то труб­ка будет обжата так, что ее сечение будет волнистым с наибольшим количеством волн вблизи заряда (рис. 138).

Хотя за последние 20 лет проблема динамической устойчивости значительно продвинулась, все же здесь осталось еще много нерешенных задач: динамическая устойчивость труб при осевой нагрузке, динамическая неустойчивость сферических оболочек и многие другие.

§ 39. Механизм разрушения

При техническом использовании взрывов среди других возникает такая проблема: как и в каких количе­ствах расположить ВВ в скальпом массиве так, чтобы после взрыва получить куски породы заданных размеров. Важно и частичное решение этой проблемы — получить при взрыве из разрушенного массива наибольшее количество кусков данного габарита. Эта проблема тесно вязана также с известной проблемой осколочных сна­рядов: надо добиться, чтобы осколки (или хотя бы большая их часть) имели заданные размеры.

Вероятностный подход. В любом реальном физиче­ском теле всегда имеется большое количество структур­ных дефектов (в том числе трещин), расположенных хаотически и имеющих различные размеры и форму. Под действием взрыва происходит раскрытие и разви­тие этих дефектов, которое и приводит к образованию осколков разнообразных форм и объемов.

В простейшем случае, когда материал в достаточно больших объемах обладает изотропными свойствами, можно описать результат осколочного действия взрыва, введя функцию распределения, т. е. вероятность того, что осколок имеет размер, меньший некоторой величи­ны. Как показывают многочисленные эксперименты, эта функция с достаточной точностью может быть представ­лена в виде:

Ф(x) = 1 - (1)

где х — характерный размер осколка, а х₀, п пара­метры распределения.

Вероятность dр того, что осколок имеет характерный размер в диапазоне

(х, х + dх), получается дифферен­цированием функции Ф(x):

dp = 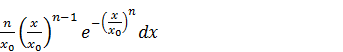(2)

Практически эта вероятность определяется как отноше­ние объема всех осколков, имеющих размер в интер­вале (x₁ x + dх), ко всему разрушенному объему:

3)

Справедливы следующие соотношения. Количество частиц, имеющих размер в интервале (х ₁ х + dх) и сред­ний объем v, равно

(4)

Относительный объем всех частиц, имеющих размер, больший х:

R = . (5)

Последнее выражение используется в горнообогатитель­ной промышленности под названием закона Рози­на—Рам мл ера (1933 г.). Из формулы (2) видно, что средний размер осколка

(6)

где Г — гамма-функция Эйлера,

. (7)

Через эту же фукцию выражается и дисперсия рас­сматриваемого распределения:

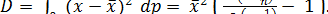(8)

При п 1 справедливы следующие приближенные соотношения:

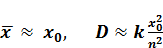(9)

(k - числовой коэффициент), раскрывающие смысл параметров x₀ и п. Мы видим, что x₀ — это «почти» средний размер осколков, а величина п характеризует «кучность» распределения относительно среднего раз­мера: чем больше п, тем более равномерно произведено дробление.

Модельные задачи. Параметр п определяется в основ­ном технологией производства взрывных работ. Вели­чину х₀ можно определять из решения модельных за­дач, причем выбор модели определяется физико-механи­ческими свойствами материала, величиной давления и геометрией конструкции. Если, например, рассматри­вается разрушение металлов под действием давления порядка 10⁵—10⁶ кг/см², то соответствующую задачу можно рассчитать по схеме идеальной несжимаемой жидкости или вязкопластической среды, в круге идей, в которых в гл. VII мы рассматривали действие куму­лятивных зарядов.

Для горных пород в большинстве случаев наиболее подходящей является модель хрупкого тела. Возможны также и комбинации различных моделей, Так, при камуфлетном взрыве в скальном грунте вблизи заряда движение грунта может описываться уравнениями сы­пучей или пластической среды, в средней зоне, разре­шенной радиальными трещинами, — уравнениями для стержней, а вдали от зарядов - уравнениями теории упругости.

Величина среднего размера осколка в каждой из моделей обычно вычисляется из исследования устойчи­вости движения по отношению к малым возмущениям синусоидального типа, причем вид движения опреде­ляется характером деформации материала. Во многих случаях разрушение тела наступает при растяжении, поэтому особый интерес представляет исследование в различных схемах устойчивости такого движения, при котором все элементы среды испытывают растяжение.

Основные результаты здесь получены для плоского движения, их можно сформулировать следующим обра­зом:

1. Растяжение упругого стержня устойчиво. Этот ре­зультат непосредственно следует из задачи, рассмотрен­ной в предыдущем параграфе (с заменой F на -F).

2. Равномерное растяжение полосы идеальной не­сжимаемой жидкости устойчиво по отношению к гар­моническим возмущениям границ, симметричных отно­сительно средней линии [6].

3. Растяжение вязкопластической полосы абсолютно неустойчиво к возмущениям указанного выше типа. Этот результат получен в пренебрежении инерционны­ми силами. При любом количестве полуволн растяже­ние приводит к разрыву [5].

Задача о трещинах. Рассмотрим теперь задачу об устойчивости трещин в упругохрупком теле. Простей­шая из возможных постановок состоит в следующем.

Пусть в плоскости (х, у) имеется система параллельных трещин длины 2l, расположенных симметрично от­носительно оси у на расстоянии h одна от другой. В на­чальный момент времени внутри трещин создается дав­ление, превосходящее равновесное и остающееся по­стоянным во все время движения. Требуется описать движение трещин и, в частности, исследовать устойчи­вость процесса.

Полного решения поставленной задачи в настоящее время нет. Можно, однако, построить приближенное ре­шение, опираясь на качественный анализ проблемы и некоторые точные решения более простых задач. Опи­шем вкратце схему решения. Сначала решается:

Статическая задача. Пусть задано растягивающее напряжение р₀, большее, чем прочность ма­териала на растяжение ; предполагается, что при этом в материале образуется система параллельных тре­щин заданной длины. Требуется определить расстояние h между трещинами.

В теории хрупких трещин показывается (см. Л. И. Седов [1]), что равновесие трещины опреде­ляется одним параметром — равновесным коэффициен­том интенсивности напряжении или модулем сцепления

, (10)

где Е модуль Юнга, — эффективная удельная энер­гия, идущая на образование единицы поверхности тре­щины, — коэффициент Пуассона (размерность этой величины МL¹/²Т^-2). Прочность материала на растяже­ние связана с величиной К₀ и длиной трещины соот­ношением

. (11)

Поставленная задача в принципе может быть ре­шена методами плоской задачи теории упрутости (см. і Н. И. М у с х е л и ш в и л и [3]). Можно показать, что в окрестности носика трещины напряжение стремится к бесконечности по закону , где s — малое расстоя­ние от носика, а К —

коэффициент интенсивности напряжений в данный момент времени. Равновесие имеет место, когда К = К₀ Точное решение в конечном виде, однако, в настоящее время не получено. Известно лишь приближенное решение

p₀ (12)

полученное для h > l, или

p₀ 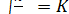(13)

для h l (В. М. Кузнецов [7]).

Наряду со статической рассматривается

Динамическая задача. Заданы длина трещин и расстояние между ними. Найти скорость при давле­ниях р, превышающих равновесное давление р₀.

Динамические задачи теории хрупкого разрушения являются более трудными, и до настоящего времени их решено очень мало даже в самых простых предполо­жениях. Имеются, однако, экспериментальные факты, использование которых помогает решению. Оказывает­ся, например, что напряженное состояние в окрестности носика движущейся трещины мало отличается от того, которое наблюдается в случае равновесной неподвиж­ной трещины. Это позволяет на каждом этапе движения трещины искать решение статической задачи, соответ­ствующей данной геометрии.

Можно, далее, показать, что скорость развития тре­щины не может превышать некоторой величины с (тео­ретически равной релеевской скорости, практически — всегда составляющей примерно половину ее). Эти сооб­ражения приводят к построению следующей формулы для скорости V движения трещины:

V = c , (14)

где с —предельная скорость, К — коэффициент интен­сивности напряжений в данный момент времени, К₀ — равновесная величина того же коэффициента (см. ра­боту [7]).

Устойчивость. Пусть в предыдущей задаче трещины через одну получили одинаковое малое приращение длины. Как изменится скорость развития трещин?

Оказывается, длинные трещины при этом ускоряют­ся, а короткие замедляются. Качественно этот резуль­тат понятен и без выкладок: длинные трещины «экрани­руют» более короткие и зажимают их. Расчет показывает, что если длина больших трещин в е раз превышает длину малых трещин, то наличие последних практически не влияет на напряженное состояние в ок­рестности' носика длинных трещин.

Короткие трещины при этом останавливаются, длин­ные— продолжают развиваться. Теперь можно рассмат­ривать развитие новой системы трещин, расстояние ме­жду которыми равно 2h. Эту систему можно подвер­гнуть возмущениям описанного типа и т. д. Таким образом, неустойчивость развития системы трещин при­водит к увеличению расстояния между ними. Если тре­щины проходят расстояние L, то число актов удвоения

равно log , а расстояние между трещинами состав­ляет

. (15)

Длинные осколки в форме пластин разрушаются так же, как стержни под действием продольного удара (см. предыдущий параграф), и при этом образуются осколки, размер которых имеет порядок h. Таким обра­зом, величина h играет роль среднего размера осколка, входящего в формулы (1), (9) и другие.

Влияние масштаба взрыва на размер осколков. Рас­смотрим два геометрически подобных взрыва в одина­ковых горных породах. Пусть все линейные размеры в одном из них в k раз больше, чем в другом. Вес ВВ, который пропорционален объемам, увеличится в k ³ раз. А как изменится средний размер куска?

В геометрически подобных точках в обоих случаях напряжения в соответствующие моменты времени будут одними и теми же. Поэтому первоначальная сетка тре­щин должна быть одинаковой. Однако время действия нагрузок, а следовательно, и время развития трещин будет больше для более крупного взрыва. В силу отме­ченной выше неустойчивости расстояние между трещи­нами будет возрастать, причем в большей степени для более мощного взрыва.

В идеализированной задаче предыдущего пункта при изменении линейного масштаба в k раз расстояние ме­жду трещинами изменялось в k ^log2 раз, так же изме­нялся и размер осколков. Мы сделаем допущение, что и в общем случае при изменении масштаба взрыва в k раз средний размер осколков изменится в 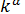раз, где 0 < а < 1.

Вот некоторые конкретные примеры.

При взрыве заряда весом 500 г в камне весом 5000 кг средний размер осколков x₀ = 19 см, а при взрыве 0, 5 г в камне весом 2130 кг средний размер x ₀ = 5 см. Так как масштаб взрыва пропорционален корню кубическому из веса ВВ, то масштаб второго взрыва был в 10 раз меньше первого; средний размер осколков изменился при этом примерно в 4 раза.

При взрыве на выброс заряда в 100 г на глубине 40 см средний размер кусков х₀ = 13, 5 см, при взрыве 20 т ВВ x ₀ = 100 см. Здесь увеличение масштаба взрыва в 60 раз привело к увеличению среднего размера кусков в 8 раз.

На основании указанных выше соображений и мно­гочисленных экспериментов была построена эмпириче­ская формула, определяющая средний размер куска в зависимости от удельного расхода ВВ и масштаба взрыва:

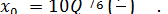(16)

Здесь x₀ измеряется в см, вес ВВ Q — в кг, объем взорванной массы V — в м³

§ 40. Равновесия в жидких средах

К числу мало изученных относится значительный цикл задачі гидродинамики и механики твердого тела, связанных с проблемой устойчивости в жидких средах. Здесь мы рассмотрим несколько примеров таких задач.

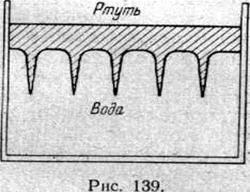
Ртуть над водой. Начнем с простейшего явления. Представим себе, что в сосуде, наполненном водой, над поверхностью воды расположен тонкий слой ртути (рис. 139). Если поверхности воды и ртути — идеальные плоскости, то ртуть будет в равновесии, однако очевид­но, что это равновесие неустойчиво. Ставится вопрос о механизме проникания ртути через воду на дно.

Физически описанное явление можно реализовать еще так: на дно закрытого стакана налить ртуть, а свер­ху нее — воду. Это равновесие устойчиво, но оно поте­ряет устойчивость, если сообщить стакану ускоренное движение вниз, с ускорением в 2—5 раз больше g.

Механизм этого явления был осознан несколько лет то­му назад за рубежом и у нас.

Приведем качественный ответ на поставленный вопрос и его принципиальное обоснование.

Займемся сначала более про­стой моделью, когда толщина слоя ртути равна или больше диаметра стакана. Здесь до­вольно очевидно, что если вследствие случайной асим­метрии в каком-то месте нижней поверхности ртути поя­вится бугорок, то этот бугорок будет расти и он обра­зует в воде воронку, по которой вся ртуть стечет вниз. Последовательные положения ртути и воды в этой постановке можно построить графоаналитическим ме­тодом.

В основной постановке, когда толщина слоя ртути мала сравнительно с диаметром стакана, процесс поте­ри устойчивости и проливания ртути вниз может на­чаться в любой точке поверхности воды. Но влияние этого процесса будет затухать по мере удаления от ме­ста слива по закону

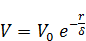, (1)

где V — скорость жидкости в некоторой точке, V₀ — ско­рость в зоне начала процесса, —толщина слоя ртути и r — расстояние рассматриваемой точки от точки слива (см. § 12).

Таким образом, части ртути, расположенные от точ­ки начавшегося слива на расстоянии более нескольких толщин слоя ртути, будут мало реагировать на начало процесса. Для этих частей найдется более близкий буго­рок, где организуется новый слив.

Поэтому при малой толщине слоя ртути ртуть устре­мится вниз по многим струйкам, расположенным друг от друга на расстоянии порядка (рис. 139).

В эту модель укладывается одно любопытное явле­ние, наблюдаемое при определенных условиях при под­водном взрыве. После взрыва под водой над гладкой поверхностью воды появляется группа фонтанчиков, расположенных друг от друга на одинаковых расстоя­ниях. Дело в том, что когда ударная волна в воде под­ходит к поверхности, то при разгрузке слой воды стремится оторваться от основной массы. Если при этом потенциальная энергия сжатия не достаточна для того, чтобы оторвать слой жидкости от ее основной массы, то мы окажемся в условиях, сходных с условиями ртути на воде, — вместо отрыва получается система фонтан­чиков.

Аналогичное явление можно наблюдать и в металле, когда ударная волна подходит к его свободной поверх­ности. Будет или не будет иметь место описанное явле­ние, зависит от ряда факторов длины ударной волны, кривизны фронта, прочности на разрыв среды и др.

Для количественного исследования описанного здесь явления можно поставить следующую задачу. Пусть слой идеальной несжимаемой жидкости < х < < у < h имеет ускорение а, направленное вертикально вверх. Пусть, далее, верхняя поверхность слоя в мо­мент t = 0 получает малое возмущение = Т₀ sin kx, которое дальше меняется по закону

(x, t) = T(t) sin kx (2)

Требуется найти дальнейшее движение свободной по­верхности.

Если толщина слоя h мала по сравнению с длиной волны возмущения, то уравнения движения можно за­менить приближенными точно так, как это сделано в гл. I для задачи о мелкой воде. Различие будет лишь в том, что ускорение силы тяжести g во всех соотноше­ниях заменится на — (в рассматриваемой здесь задаче ускорение направлено вверх). В частности, для свободной поверхности жидкости получится уравнение.

(3)

Подставляя в него выражение (2), найдем

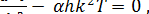(4)

откуда

T = A (5)

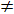где А и В — постоянные. Начальные условия для T имеют вид T(0) = Т₀, Т" (0) = , откуда следует, что A 0. Поэтому амплитуда колебаний (2) неограниченно возрастает и движение оказывается неустойчивым.

В нашем приближении неустойчивы возмущения любой длины волны = . В действительности же очень мелкие волны должны затухать вследствие действия сил поверхностного натяжения, и неустойчивыми являются только гармоники, длина волн которых превышает некоторую критическую величину λ _min. Эту величину и следует считать характерным расстоянием между фонтанчиками в рассмотренных здесь явлениях; расчеты [6] дают для нее приближенную формулу

λ _{min = 2 .} (6)

где коэффициент поверхностного натяжения, а p — плотность жидкости.

Образование волн. Проблеме образования ветровых волн посвящено огромное количество статей, обзоров и монографий. Каков механизм образования волн при заданном ветровом режиме, существует ли обратная связь, т. е. влияют ли в свою очередь волны на ветровой режим? Эти и многие другие вопросы не решены до сих пор, хотя качественная картина была ясна уже давно.

Свободная поверхность воды, при наличии над ней воздушного потока, неустойчива: при малых случайных колебаниях давление во впадинах по закону Бернулли больше, чем на выступах, поэтому каждое волновое движение под действием ветра должно прогрессировать. Этот результат легко получить и аналитически (см. например, Ландау и Лифшиц [2]). Если обозначить через V скорость ветра, Р₀ — плотность воды, р - плотность воздуха, λ —длина волны, то рост амплитуды волны определяется множителем , где

(7)

С другой стороны, если высота волны становится порядка своей длины, то гребень волны срывается ветром и преимущества роста приобретают волны большей длины В этих условиях по истечении достаточно большого времени должен наступить установившийся режим. Можно показать, что для этого скорость ветра должна быть вдвое больше скорости волн.

В самом деле, естественно предположить, что здесь (как в задаче обтекания траншеи из § 22) между каждыми двумя соседними горбами волны имеется зона вихревого движения (рис. 140). Перейдем к системе координат, связанной с волной. В этой системе скорость течения жидкости равна скорости движения волны и направлена в отрицательную сторону. В силу не прерывности поля скоростей на границе вихревой зоны скорость ветра тоже должна быть равной С, но направлена в положительную сторону. Переходя снова к неподвижной системе координат, получаем доказательство высказанного утверждения.

Наряду с теоретическими работами проводилось много наблюдений ветровых волн в натурных условиях. Лет 20 назад в Крыму был построен специальный «штормовой бассейн» с вертикальными круговыми цилиндрическими стенками. Над свободной поверхностью там расположено несколько мощных компрессоров, которые способны создавать ветер в большом диапазоне скоростей. Волны в этом штормовом бассейне действительно образуются, но их характер существенно отличен от нормальных ветровых волн, при образовании которых ветер имеет достаточно стабильную направленность. В кольцевом бассейне образовавшиеся волны имея определенную направленность в зоне зарождения, очень быстро переходят в колебания воды в направлении оси бассейна — создаются группы стоячих волн.

Очень интересно наблюдать, но трудно рассчитать явления, которые связаны с кольцевыми волнами. Отметим одно из них — если каким-либо образом, например, шнуровым зарядом ВВ, имеющим форму окружности, создать кольцевую волну (кольцевую выпуклость или кольцевую яму), то в стороны от центра кольца волны будут распространяться с обычным законом затухания. Но в сторону центра длина волны будет меняться медленно, и не будет обычного расщепления волны па более мелкие. В соответствии с этим высота волны при приближении к центру будет нарастать и даст всплеск по высоте, в несколько раз превышающей начальную высоту волны.

Устойчивость струй. В круге идей, рассмотренных выше, имеется большая группа задач по устойчивости жидких струй. Классической является проблема устойчивости водяной струи в воздухе. В частности, если заданы выходная скорость и диаметр струи, то какой высоты можно достигнуть струей? Какого расстояния можно достигнуть струей?

В этих постановках воду можно рассматривать как идеальную жидкость. При скорости струи, близкой скорости звука в воздухе, естественно будет существенным фактор сжимаемости воздуха. До сих пор до конца не решена проблема затопленной струи — водяной струи, движущейся в воде; в этом случае существенным фактором является вязкость, а при значительных скоростях — турбулентность.

Сюда же относится весьма интересная как принципиально, так и с точки зрения приложений проблема устойчивости жидкого стержня при одновременном растяжении и закручивании. Пусть дана осесимметричная рубка из мягкого железа или меди, осевое сечение которой имеет синусоидальный характер; диаметр трубки 10—15 мм, толщина стенки 1—1, 5мм.

Опишем, как можно изготовлять такие трубки. Вытачивается матрица, внутренняя поверхность которой совпадает с внешней поверхностью будущей трубки. В мат­рицу вставляется цилиндрическая трубка, которая гер­метически закрыта с одного конца, а с другого конца матрицу нужно завинтить крышкой с небольшим отвер­стием по оси (рис. 141). В это отверстие под большим давлением нагнетается вода, в результате чего внешняя поверхность вставленной трубки вплотную подходит к матрице. При таком способе отштампованная трубка

будет иметь переменную толщину стенок; чтобы избе­жать этого, вставляемый в матрицу цилиндр следует предварительно немного выточить снаружи в нужных местах.

Рассматривается два случая: когда трубка пустая и когда она заполнена водой. В каждом случае трубка растягивается в направлении своей оси и, кроме того, при постоянном растяжении она еще закручивается, причем скорость закручивания меняется. Требуется вы­яснить, в каких случаях волны на поверхности трубки будут сглаживаться (устойчивость) и в каких они будут нарастать (неустойчивость).

Качественно довольно ясно, что при простом растя­жении (или растяжении с достаточно малым закручи­ванием) мы получим устойчивый процесс — волны на поверхности трубки будут сглаживаться. В самом деле, растягивающая сила будет увеличивать диаметр сече­ний трубок в шейках и уменьшать диаметр сечений в пучностях.

Все изменится, если наряду с растяжением трубка достаточно сильно закручивается. Волокна трубки, рас­положенные в ее осевом сечении, превратятся в спи­рали, а растяжение будет сжимать эти спирали, осо­бенно сильно в узких местах, соответствующих шейкам трубки. Это приведет к дальнейшему сжатию шеек, и процесс будет неустойчивым.

Очень желательно построить количественную модель описанного явления. Предварительно следует выяснить статическую и динамическую устойчивость стержней и трубок (упругих и с пластичностью) при чистом закру­чивании. При этом нужно рассмотреть два случая: а) расстояние между торцами трубки или стержня не меняется, б) действуют только крутящие силы.

Взрыв в воде. Здесь будут описаны три явления, наблюдаемых при взрыве в воде. Для них не построено количественных теорий и даже качественно еще не все в них ясно.

1) Выше говорилось о том, что если цилиндриче­скую трубку, заделанную с обеих концов, опустить вер­тикально в воду и под ней произвести взрыв, то трубка обожмется по законам потери ди­намической устойчивости — сечение трубки примет волновой характер, причем частота волн будет убывать но мере удаления от нижнего кон­ца. Это явление мы объяснили про­стой приближенной схемой.

Однако в этом эксперименте об­наруживается еще одно интересное

явление, которое не укладывается в простейшую схе­му, — обжатая трубка (см. рис. 138) имеет вид туго за­плетенной косы! Как объяснить это явление?

2) Возьмем сферическую оболочку из упругого ма­териала (например, надутый воздухом мяч) и погрузим ее в резервуар с водой, в котором можно создавать большие давления (рис. 142). Считая, что материал ста­новится пластичным за пределами упругости, найти по его характеристикам: а) критическое давление, при ко­тором происходит потеря упругости, б) форму сфериче­ской оболочки после того, как она потеряет устойчи­вость, в) форму потери устойчивости в случае, если дав­ление в воде мгновенно превысит в п раз критическое.

Словом, задача состоит в том, чтобы перенести на случай сферической оболочки схемы статической и ди­намической неустойчивости, которые выше рассматрива­лись для случая стержней (в связи с этим см. [8]).

3) В одной из стенок толстостенного бака имеется круглое отверстие, в которое можно вставлять тонкие мембраны различной толщины и из разных материалов (железо, медь, свинец и др.). В центре бака, против за­крытого мембраной отверстия, производятся взрывы различной мощности, причем после каждого взрыва прогнутая мембрана заменяется новой (рис. 143).

В одной серии опытов был обнару­жен следующий парадоксальный эф­фект. При увеличении заряда прогиб мембраны увеличивался до определен­ной величины, а при дальнейшем уве­личении заряда прогиб еще увели­чился, но изменил направление — мем­брана оказывалась прогнутой навстре­чу взрыву!

Качественно явление можно объяснить так. При по­тере устойчивости под действием взрыва па мембрану (как и на стержень, случай которого был рассмотрен в начале главы) действует сила F не только переменной величины, но и переменного направления. Когда F на­правлена во внешность бака, она дает прогиб вовне, а когда внутрь, то и мембрана прогибается вовнутрь. Для построения схемы этого явления нужно прежде всего изучить вопросы потери устойчивости круговых мембран, закрепленных на краю.

Литература

1. Л. И. Cедов, Механика сплошной среды, т. II. «Наука», 1970.

2. Л. Д. Ландау, Е. М. Лифшиц, Механика сплошных сред, Физматгиз, 1963.

3. Н. И. Мусхелишвили. Некоторые основные задачи математи­ческой теории упругости, «Наука», 1966.

4. М. А. Лаврентьев, А. Ю. Ишлинский, Динамические формы потери устойчивости упругих систем, ДАН СССР, 65, № 6, 1949.

5. А. Ю. Ишлинский, Об устойчивости вязкопластического тече­ния полосы и прута, ПММ, т. VII, вып. 2, 1943.

6. В. М. Кузнецов, Е. Н. Шер, Об устойчивости течения идеаль­ной несжимаемой жидкости в полосе и кольце, ПМТФ, № 2, 1964.

7. В. М. Кузнецов, О нестационарном распространении системы трещин в хрупком материале, ПМТФ, № 2, 1968.

8. А. В. Погорелов, Геометрические методы в нелинейной теории упругих оболочек, «Наука», 1967.