Метод функционала плотности

Наиболее эффективным, является метод расчета структуры и свойств молекул, который использовал бы только информацию о конфигурации электронных оболочек атомов, составляющих систему. Этот метода позволил бы ученым предсказывать существование и свойства новых материалов, еще не полученных экспериментально.

Первопринципныеметоды (аb-initio) используют этот механизм, но за счет большой сложности расчётов в них также применяются приближения. При этом существует высокая точность расчетов.

К основным методам первопринципных расчетов можно отнести следующие: метод Хартри-Фока и метод функционала электронной плотности.

Одним из самых первых методов является метод Хартри-Фока для расчета атомов и молекул, в связи с чем получил широкое распространение.

Однако при использовании этого метода, для больших систем возникают трудности из-за огромного количества перекрестных обменных интегралов. Кроме того, этот метод, учитывает обменное взаимодействие и не учитывает корреляционные эффекты, что делает его использование для расчётов электронной структуры некорректным, причем для поверхностей эти приближения подходят еще меньше, чем для объемных кристаллов.

В следствии этого в данной работе расчеты производились с использованием метода функционала электронной плотности (DFT).

В основе метода DFT лежит теорема Хоэнберга-Кона о том, что между электронной плотностью р в данной системе и ее электронной энергией существует однозначное соответствие, и электронная энергия основного состояния всецело определяется электронной плотностью. Применение метода функционала плотности непосредственно в вычислительной химии стало возможным с введением орбитального приближения Кона и Шэма.

Поскольку плотность ρ (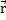) определяет как число частиц N, так и потенциал взаимодействия электронов с внешним полем V_ee(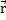) (с точностью до несущественной аддитивной постоянной), с помощью нее можно получить полный гамильтониан H и оператор числа частиц N для электронной системы.

Следовательно, ρ (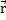) неявно определяет свойства, получаемые из гамильтониана путем решения уравнения Шредингера зависящего или не зависящего от времени.

Таким образом, функционал полной энергии может быть записан в виде:

𝐸 [𝜌 (𝑟)] = 𝑇 [ρ (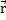)]+ U_ee[ρ (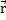)] + 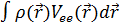, (1)

где 𝑇 [ρ (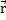)] – учитывает кинетическую энергию электронов, U_ee[ρ (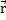) ] - энергию межэлектронного взаимодействия, V_ee(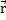) - потенциал, описывающий взаимодействие электронов с внешним полем. Минимизируя энергию относительно одноэлектронных орбиталей, можно получить уравнения Кона - Шема аналогичные уравнениям Хартри - Фока:

ℎ _{𝑘 𝑠} 𝜑 _𝑖 = 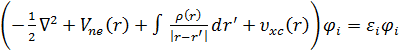, (2)

здесь h_ks - одноэлектронный оператор Кона-Шема, аналогичный оператору Фока, в уравнениях Хартри-Фока, ε _i - энергия канонических одноэлектронных орбиталей Кона-Шема, 𝜑 _𝑖 - канонические одноэлектронные орбитали Кона-Шема, V_ne - потенциал электронно-ядерного взаимодействия и v_xc - обменно-корреляционный потенциал.

Различные методы функционала плотности отличаются формой обменно-­корреляционного функционала. Как правило, этот функционал выражается через плотность корреляционно-обменной энергии ε _xc:

𝑉 𝑥 𝑐 𝑟 = 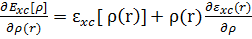(3)

Корреляционно-обменная плотность энергии s_xc может быть представлена как сумма корреляционной s_c и обменной s_x энергий.

Метод функционала плотности реализуется с помощью одного из трех приближения, от которых зависит вид обменно-корелляционного функционала.