
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Розрахунки припливу води до водозабiрних споруд
|
|
Серед водозбiрних споруд ми будемо розглядати такi гiрничi виробки, як дрени (канави) i свердловини. В гiдрогеологiї гiрничi виробки подiляють на досконалi i недосконалi.
Гiдродинамiчно д о с к о н а л о ю називається гiрнича виробка, яка проходить водоносний горизонт вiд покрiвлi до пiдошви. Приплив води до неї вiдбувається по всiй поверхнi дотикання стiнок виробки до водоносного горизонту, потужністю Н (мал. 34, а). Якщо ж виробка не доходить до водотриву, вона називається недосконалою за ступенем виявлення водоносного горизонту (мал. 34, б). Часто виробки закрiплюються вiд обвалювання, цементуються, свердловини обладнуються обсадними трубами, фiльтрами тощо. Звичайно, що приплив води до таких виробок затруднений i їх називають недосконалими за характером виявлення водоносного горизонту. Дуже часто на практицi ми маємо справу з комбiнацiєю недосконалостей.

Мал.34. Схема досконалої (а) і недосконалих (б, в) свердловин
Основнi рiвняння припливу води до водозаборiв (свердловин та дрен) будемо виводити за умови д о с к о н а л о с т і виробок.
Уявимо собi плоский потiк грунтових вод (мал. 35). Гiдравлiчний градiєнт I в даному випадку дорiвнює
 (32)
(32)
де х - вiддаль мiж перерiзами h 1 i h 2.
Мал.35. Схема плоского потоку грунтових вод
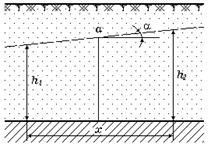
Якщо ми будемо зближувати перерiзи h 1 i h 2 так, щоб вiддаль мiж ними стала рiвною нулю, то отримаємо уклон (гiдравлiчний градiєнт) в точцi a, який дорiвнює тангенсу кута нахилу дзеркала грунтових вод або першiй похiднiй
 (33)
(33)
Пiдставивши отриманий вираз гiдравлiчного уклону у вираз закону Дарсi (31), отримаємо:
для безнапiрних вод
 (34)
(34)
для напiрних вод
 (35)
(35)
де Н - напiр, який вiдраховується вiд пiдошви водоносного пласту до його п’єзометричного рiвня.
Розрахунок припливу грунтових вод до досконалої горизонтальної дрени (канави). На мал. 36 штриховою лiнiєю показано положення дзеркала грунтових вод до проходки дрени (статичний рiвень). Пiсля проходки дрени швидкiсть руху води в нiй збiльшується i рiвень води понижується на величину S, яку в гiдрогеологiї прийнято називати величиною пониження. Iншими словами, величина пониження є рiзницею мiж статичним i динамiчним рiвнями. Потужнiсть водоносного горизонту до пониження позначимо через H, глибину води в дренi - через h 0. Внаслiдок пониження рiвня в дренi в водоносному горизонтi утворюється депресiйна лійка, показана на мал. 36 суцiльною жирною лiнiєю. Вiддаль R, на яку поширюється вплив пониження, називають радiусом впливу.
Для розрахунку припливу води Q в дрену вибираємо на вiддалi x вiд стiнки дрени перерiз з напором h, який знаходиться в iнтервалi вiд 0 до R.

Мал.36. Схема до розрахунку припливу води в досконалу дрену в безнапірному водоносному пласті
В загальному виглядi приплив води до дрени буде дорiвнювати виразу (34). Пiдставимо сюди величину площi фiльтрацiї
F = Bh, (36)
де В - довжина дрени. Отримаємо
 (37)
(37)
При розрахунку припливу води в дрену зручно користуватись поняттям одиничного припливу q, тобто припливу води на одиницю довжини дрени
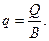 (38)
(38)
Звiдси елементарна формула для розрахунку припливу води
 (39)
(39)
Роздiлимо змiннi у виразi (47), тобто помножимо обидвi його частини на dx i проiнтегруємо
 (40)
(40)
В результатi отримаємо
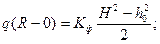 (41)
(41)
 (42)
(42)
 (43)
(43)
Формула (42) виражає величину одиничного припливу з одного боку дрени. Щоб отримати повний приплив води в дрену, необхiдно помножити одиничний притiк на два, а потiм - на довжину дрени. Приплив води в торцi дрени як правило не враховують, так як вiн при великiй довжинi дрени складає незначну частину.
За формулою (42) можна розрахувати витрату плоского грунтового потоку. Пiдставивши замiсть радiуса впливу вiддаль мiж перерiзами, рiвну l (мал. 37), отримаємо
 (44)
(44)
Вираз  можна записати так
можна записати так
 (45)
(45)

Мал.37. Схема до розрахунку витрати плоского потоку грунтових вод
тобто одинична витрата дорiвнює
 (46)
(46)
а повна витрата складе
 (47)
(47)
де hc - h середнє.
Дослiджуючи вираз (51), ми зможемо вирiшити одну з дуже важливих задач в гiдрогеологiчних розрахунках - вивести рiвняння депресiйної кривої. Побудова депресiйної кривої необхiдна при виникненнi загрози затоплення пiдземними водами котлованiв, пiдвалiв будинкiв тощо (мал. 38).

Мал.38. Схема до розрахунку депресійної кривої потоку грунтових вод
Змiнивши границi iнтегрування у виразi (48) по X вiд 0 до х, а по Y вiд h 0до h, отримаємо
 (48)
(48)
Очевидно, що приплив води у виразах (43) i (48) одинаковий, тобто
 (49)
(49)
Вирiшуючи (57) вiдносно h, маємо
 (50)
(50)
Для побудови депресiйної кривої ми задаємось величиною h 0 в залежностi вiд S, потужнiсть водоносного горизонту H легко отримати за даними бурiння, величину радiуса впливу можна вирахувати за емпiричними формулами (про це ми поговоримо пiзнiше).
На мiлiметровому паперi будуємо розрiз через дрену i котлован (мал. 38) i, задаючись рiзними значеннями x (x 1, x 2,..., x n), наприклад: 10, 20, 30 i т. д. метрiв, отримуємо величини h (h 1, h 2,..., h n). З’єднавши отриманi точки плавною лiнiєю, отримаємо криву депресiї. Якщо вона проходить через котлован, будуємо нову криву, задавшись бiльшим значенням пониження i, природно, меншим значенням глибини води в дренi. Побудову ведемо до тих пiр, доки депресiйна крива не опуститься нижче дна котлована. Тепер залишається понизити рiвень води в дренi на останню величину S i котлован при будiвництвi буде сухим.
Розрахунок припливу грунтових вод до досконалої свердловини. Тут ми маємо справу не з плоским потоком, як в попередньому випадку, а з радiальним. На мал. 39 показанi всi позначення, якi нам зрозумiлi з попередньої задачi, крiм r - радiуса свердловини.

Мал.39. Схема до розрахунку припливу грунтових вод до досконалої свердловини
Розрахунок починаємо з рiвняння (37). Площа притоку води через перерiз h дорiвнює площi бокової поверхнi цилiндра, радiус якого дорiвнює x, тобто
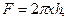 (51)
(51)
 (52)
(52)
Роздiлимо змiннi (тобто помножимо обидвi частини рiвняння на ( ) i iнтегруємо
) i iнтегруємо
 (53)
(53)
Iнтегрування по Х проводимо не вiд нуля, а вiд r - стiнки свердловини, в результатi отримуємо формулу Дюпюi
 (54)
(54)
 (55)
(55)
У такому виглядi користуватись виразом (55) не зовсiм зручно, так як у ньому присутнiй натуральний логарифм. Пiдставимо замiсть нього десятковий (ln x =2, 30lg x), а замiсть p його значення i отримаємо зручніший вираз для розрахунку припливу безнапiрних вод до свердловини:
 (56)
(56)
Вираз  можна видозмiнити:
можна видозмiнити:
 (57)
(57)
i, пiдставивши його в залежнiсть (56), отримаємо

 (58)
(58)
Для отримання рiвняння депресiйної кривої повернемось до (52) і змiнимо границi iнтегрування по Х вiд r до x, а по Y вiд h 0 до h:
 (59)
(59)
 (60)
(60)
Вирiшуємо рiвнiсть вiдносно h i отримуємо рiвняння кривої депресiї
 (61)
(61)
Розрахунок водопониження при взаємодiючих свердловинах. При проходцi котлованiв пiд споруди часто доводиться вiдкачувати з них воду для пониження рiвня грунтових вод. В таких випадках, як правило, замiсть вiдкачування води з самого котлована, що часто буває малоефективно, застосовують пониження за допомогою взаємо-дiючих свердловин. В з а є м о д і ю ч и м и називають свердловини, в яких сума радiусiв впливу бiльша вiд вiддалi мiж ними (мал. 41).

Мал.41. Взаємодіючі свердловини
Взаємодiя водозаборiв досить складна. Розглянемо приклад взаємодії двох свердловин, розташованих на відстані L (мал.41). Як ми бачимо, віддаль L менша від радіусів впливу R 1 та R 2. При відкачці води із свердловини 1 рівень води в ній знизиться на величину S 1. В свердловині 2 рівень понизиться на величину s 1. При пониженні в сердловині 2 рівня на S 2, в свердловині 1 рівень знизиться на величину s 2.
При одночасному відборі води з обох свердловин депресійні лійки накладуться одна на одну, рівень води між свердловинами знизиться ще більше і крива депресії займе положення, показане на мал. 62 штрих-пунктирною лінією. Чим більше ми будемо зближувати свердловини, тим більше пониження буде досягнуте. При цьому дебіт кожної з цих взаємодіючих свердловин Q 1 буде меншим від того, яким він був би в кожної окремої одиночної свердловини Q.
Зменшення дебіту оцінюється величиною інтерференції d.
 (62)
(62)
Зрозуміло, що при L=R 1 +R 2 або L=2R взаємодії свердловин не відбудеться, інтерференція буде рівною одиниці і зниження депре-сійних кривих не відбудеться. При зменшенні відстані між свердлови-нами буде зменшуватись і величина інтерференції. Так при відстані, яка дорівнює R; 0, 5 R; 0, 2 R; 0, 02 R та 0, 002 R інтерференція, відповідно, складе 0, 97; 0, 90; 0, 81; 0, 64 та 0, 53 (за Л.С. Лейбензоном).
При бурінні групи свердловин, призначених для водопостачання, з метою зменшення довжини водопровідних труб, доцільно свердло-вини розташовувати на відстані, рівній половині радіуса впливу.
При осушенні, коли основною метою є пониження депресійної кривої між свердловинами, їх бурять на відстані 0, 1 R.
Пониження рiвня грунтових вод можна розрахувати за методом Форхгеймера. Приймемо, що свердловини роташованi навколо котлована (А) так, як зображено на мал. 42.
Розрахунок для однiєї свердловини почнемо з формули (55), дещо її змiнивши

Мал.42. Схема розташування свердловин для пониження рівня грунтових вод у котловані
 (63)
(63)
При одночаснiй роботi всiх свердловин загальне рiвняння депре-сiйної кривої набуде вигляду
 (64)
(64)
Якщо всi свердловини мають однаковi радiуси, однаковi вiддалi вiд котловану, однаковi дебiти та пройденi в породах з однаковим коефiцiєнтом фiльтрацiї, то розрахунок за цiєю формулою набагато спрощується.
Розрахунок припливу напiрних вод в досконалу дрену. На мал. 43 подана схема розрахунку, де введенi новi для нас позначення:
H - напiр i m - потужнiсть водоносного горизонту (всi iншi позначення - попереднi).
Площа фiльтрацiї в перерiзi h, що знаходиться на вiддалi x вiд стiнки дрени, буде дорiвнювати
F = Bm. (65)

Мал.43. Схема припливу артезіанських вод до досконалої дрени
Ми тут знову не враховуємо притiк води через торцi дрени. Пiдставимо площу в (35):
 (66)
(66)
Переходимо до одиничної витрати
 (67)
(67)
Роздiливши змiннi i проiнтегрувавши, отримуємо
 (68)
(68)
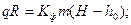 (69)
(69)
 (70)
(70)
Вираз (70) являє собою одиничний приплив артезiанських вод в один iз бортiв канави. Повний приплив складе
 (71)
(71)
Якщо нам потрiбно отримати рiвняння депресiйної кривої, то (68) потрiбно проiнтегрувати по X вiд 0 до х, а по Y вiд h 0 до h:
 (72)
(72)
 (73)
(73)
 (74)
(74)
Рiшаємо рiвняння (74) вiдносно h:
 (75)
(75)
Аналiзуючи вираз (75), ми бачимо, що це рiвняння прямої лiнiї. Насправдi ж депресiйна крива криволiнiйна.
Розрахунок припливу артезiанських вод у досконалу свердловину. Розрахунок припливу артезiанських вод у досконалу свердловину зображений на мал. 44. У вираз (52) пiдставляємо величину площi фiльтрацiї, яка в перерiзi h дорівнює
F = 2π xm, (76)
 (77)
(77)

Мал.44. Схема припливу артезіанських вод в досконалу свердловину
Роздiливши змiннi i iнтегруючи по X вiд r до R, а по Y вiд h 0 до H, отримаємо
 (78)
(78)
 (79)
(79)
 (80)
(80)
Перевiвши натуральний логарифм в десятковий, i ввiвши числове значення p, отримуємо вираз для розрахунку припливу артезiанських вод в досконалу свердловину:
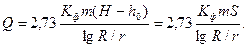 (81)
(81)
Для розрахунку кривої депресiї повернемось до (78) i змiнимо границi iнтегрування: по X вiд r до x, а по Y вiд h 0 до h: 
 (82)
(82)
Приплив у виразах (80) i (82) однаковий:
 (83)
(83)
Знаходимо h:
 (84)
(84)
тобто ми знову отримали рiвняння прямої лiнiї, хоча в природних умовах депресiйна лійка в розрiзi має вигляд кривої.
Всi вищенаведенi формули дуже простi i можуть служити лише для приблизних розрахункiв. В гiдрогеологiчнiй практицi застосо-вуються формули, якi враховують уклони водотривких пластiв, неоднорiднiсть в водопроникностi шарiв порiд, поправки на недоско-налiсть свердловин, на несталий рух тощо. Розглянемо деякі з них.
В и т р а т а п л о с к о г о п о т о к у. При похилому водотриві (мал.45) розрахунок проводять з врахуванням додаткової горизон-тальної площини О-О. Якщо потужність водоносного горизонту залишається постійною, то розрахунок витрати проводиться за залежністю
 (85)
(85)
у випадку непостійної потужності водоносного горизонту розрахунок проводиться за рівнянням
 (86)
(86)
 |
де B - ширина потоку, hс - середня потужність водоносного горизонту, H 1 і H 2 - перевищення дзеркала грунтових вод в перерізах над порівняльною площиною, h 1 і h 2 - потужності водоносного горизонту та l - відстань між перерізами.
До недосконалого колодязя (свердловини) вода припливає через його стінки та дно, що дещо ускладнює розрахунок (мал.46). Дебіт таких виробок завжди менший від дебіту досконалих виробок. При відкачці вода поступає в колодязь лише із частини водоносного горизонту, котру називають активною зоною (Н0). Глибину активної зони приймають за 4/3 висоти стовпа води в колодязі до відкачки (Р), тобто Н0= 4/3 Р. За формулою Дюпюі, доповненою Паркером
 (87)
(87)
Приплив до недосконалої дрени теж завжди менший від припливу води до досконалої дрени. Його можна розрахувати за рівнянням
 (88)
(88)

де Qнед. - витрата недосконалої дрени; Qдоск. - витрата досконалої дрени; t - віддальвід дна канави до статичного (нормального) рівня води; Н - потужність водоносного горизонту грунтових вод.
Розрахунки припливу води до котлованів. При проходці котлованів часто доводиться відкачувати з них воду, тому зупинимось на деяких методах розрахунку припливу води до таких виробок.
Котлован прямокутний, витягнутої форми, довжиною B, досконалий (мал.47). В такому випадку застосовується формула

 (89)
(89)
Якщо потужності водоносного горизонту з обох боків котловану не однакові, тобто вони складають Н 1 та Н 2, то використовують рівняння

 (90)
(90)
Якщо ж котлован квадратний або близький до того, то в такому випадку площу його перерізу прирівнюють до площі круга з радіусом
r 0. Так як  то приплив води до котловану складе
то приплив води до котловану складе
 (91)
(91)
Приплив води до котловану, доведеного до водотриву, котрий розташований біля річки (мал.48), розраховують за формулою

 (82)
(82)
де Q - сумарний приплив води в котлован; qв - приплив води з боку вододілу; qр - приплив води з боку річки; В - довжина котловану; R - радіус депресійної лійки, яка утворюється котлованом в дзеркалі грунтових вод; l - відстань від котловану до річки; Н - потужність безнапірного водоносного горизонту; Нр - перевищення рівня води в річці над водотривом.
Якщо котлован прямокутний, недосконалий, заглиблений на величину l в безнапірний водоносний горизонт (мал.49), то застосо-вується наближена формула Н.К. Гіринського

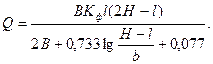 (93)
(93)
Існує ще багато різних, інколи дуже складних формул для розрахунку припливу води до гірничих виробок. Формули врахо-вують всілякі нюанси гідрогеологічних умов і наведені вони в спеціальній літературі.
Поняття про дебiт i питомий дебiт. Дебiт (французькою - збуватись, витрата) - кiлькiсть води, нафти, газу, яка видається джерелом, колодязем або свердловиною за одиницю часу. Одиницями вимiрювання дебiту для пiдземних вод є м3/с або м/добу, для нафти - т/добу.
Питомий дебiт отримують вiд дiлення величини дебiту на величину пониження рiвня
 (94)
(94)
i звичайно вимiрюють в м2/добу.