
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определения функции от матрицы.
|
|
Определение 1. Приведем некоторые примеры формул, по которым ведется вычисление основных функций на ЭВМ:
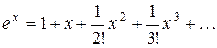 (4.1)
(4.1)
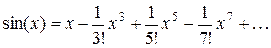 (4.2)
(4.2)
 , (4.3)
, (4.3)
где x – аргумент функции.
Аналогично можно задать функции от матриц:
 (4.4)
(4.4)
 (4.5)
(4.5)
 , (4.6)
, (4.6)
где  – матрица (аргумент функции).
– матрица (аргумент функции).
Определение 2. В большинстве случаев, за редким исключением, квадратная матрица  -го порядка может быть представлена в виде произведения:
-го порядка может быть представлена в виде произведения:
 , где
, где  , (4.7)
, (4.7)
 – собственные числа матрицы
– собственные числа матрицы  ;
;  – матрица, столбцы которой являются соответствующими собственными векторами.
– матрица, столбцы которой являются соответствующими собственными векторами.
Из разложения (4.7) следует:
 ;
;  ; …
; …
 , (4.8)
, (4.8)
где
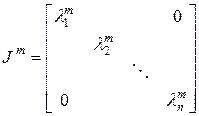 . (4.9)
. (4.9)
Подставив  в формулы (4.4)-(4.6), получим:
в формулы (4.4)-(4.6), получим:
 ; (4.10)
; (4.10)
 ; (4.11)
; (4.11)
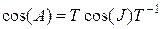 , (4.12)
, (4.12)
где
 ;
;  ;
;
 . (4.13)
. (4.13)
Данные преобразования позволяют записать общую формулу для определения функций от матрицы, которая существенно упрощает процесс вычисления:
 , (4.14)
, (4.14)
где
 ; (4.15)
; (4.15)
 – собственные числа матрицы
– собственные числа матрицы  ,
,  – матрица, столбцы которой являются соответствующими собственными векторами матрицы
– матрица, столбцы которой являются соответствующими собственными векторами матрицы  , n – порядок квадратной матрицы
, n – порядок квадратной матрицы  .
.
Замечание 1. Самый общий случай представления квадратной матрицы в виде произведения также имеет вид жорданова разложения
 (4.16)
(4.16)
но при этом матрица Жордана  имеет квазидиагональный вид:
имеет квазидиагональный вид:
 ,
,  ;
;  ,
,
где  – жорданова клетка; матрица
– жорданова клетка; матрица  состоит из столбцов, часть которых является собственными векторами, а часть присоединенными (или корневыми) векторами, при этом
состоит из столбцов, часть которых является собственными векторами, а часть присоединенными (или корневыми) векторами, при этом
 , (4.17)
, (4.17)
где
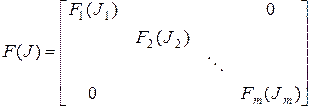 ; (4.18)
; (4.18)
 , (4.19)
, (4.19)
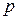 – порядок k -ой жордановой клетки.
– порядок k -ой жордановой клетки.
Более подробно данный вопрос рассматривается в специальной литературе по линейной алгебре.
Дополнительный вид определения функции от матрицы. В случае, если порядки всех жордановых клетки равны единице тогда:
 ,
,
где
 ; (4.20)
; (4.20)
 – собственный вектор матрицы
– собственный вектор матрицы  , т.е.
, т.е.
 , (4.21)
, (4.21)
где 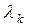 – собственное число; при соответствующей нормировке
– собственное число; при соответствующей нормировке
 . (4.22)
. (4.22)
Очевидно, что матрица Жордана  представима в виде разложения
представима в виде разложения
 . (4.23)
. (4.23)
Матрица  имеет вид:
имеет вид:
 , (4.24)
, (4.24)
где  – k -я вектор-строка матрицы
– k -я вектор-строка матрицы  .
.
Тогда матрица  может быть представлена следующим образом:
может быть представлена следующим образом:
 , (4.25)
, (4.25)
где
 (4.26)
(4.26)
– оператор проектирования представимый в виде
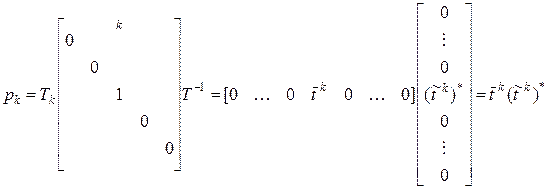 . (4.27)
. (4.27)
Покажем, что
 . (4.28)
. (4.28)
Вследствие (4.26) имеем:
 .
.
Произведение 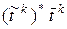 является результатом умножения k -ой строки матрицы
является результатом умножения k -ой строки матрицы  на k -й столбец матрицы
на k -й столбец матрицы  . В тоже время, как известно,
. В тоже время, как известно,  . Следовательно,
. Следовательно,  , что доказывает формулу (4.28).
, что доказывает формулу (4.28).
Соответственно функция от матрицы будет иметь вид:
 (4.29)
(4.29)
В частности, справедливы формулы:
 ;
;  ;
;  . (4.30)
. (4.30)
Такая запись применяется, к примеру, для получения общего решения задачи динамики.
Замечание 2. Функции от матриц являются необходимым средством решения систем дифференциальных уравнений.