Задачи для индивидуального задания.

Задание 1

Задачи линейного программирования, решаемые геометрическим методом.

1.1) ,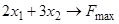

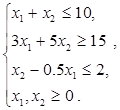
1.2) ,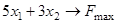

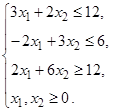
1.3) ,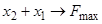

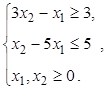
1.4) ,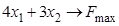

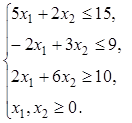
1.5) ,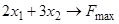

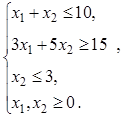
1.6) ,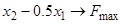

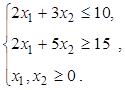
1.7) ,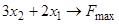

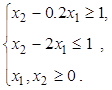
1.8) ,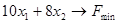

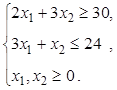
1.9) ,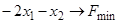

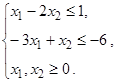
1.10) ,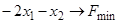

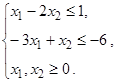
Задание 2

Примеры решения задач линейного программирования симплексным методом.

Задача 1.Максимизировать функцию 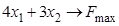при следующих ограничениях,

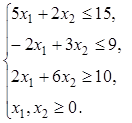
Задача 2.Максимизировать функцию 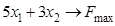при следующих ограничениях

.

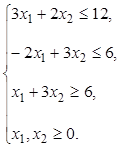Задачи для контрольной работы.

2.1). , .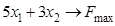

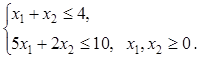2.2). ,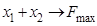

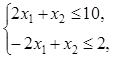
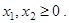
2.3). ,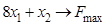

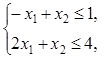
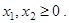
2.4). ,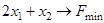

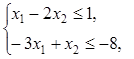
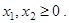
2.5). ,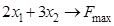

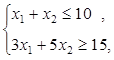
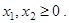
2.6). ,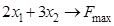

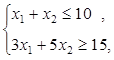
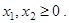
2.7). , .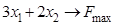

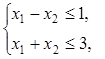
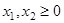2.8). , .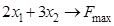

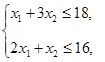
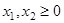2.9). , .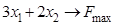

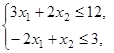
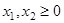2.10). , , .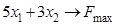

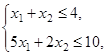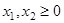Задачи для индивидуального задания.

Далее везде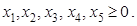

ИЗ-1.

ИЗ-2. ,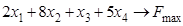

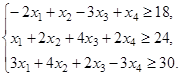
ИЗ-3. ,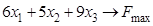

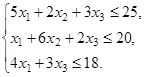
ИЗ-4. ,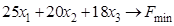

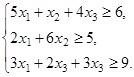
ИЗ-5. ,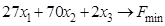

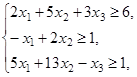
ИЗ-6. ,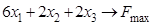

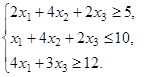
ИЗ-7. ,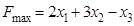

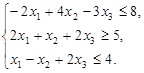
ИЗ-8. ,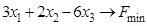

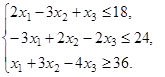
ИЗ-9. ,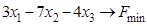

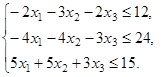
ИЗ-10. ,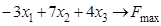

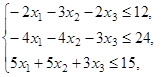
ИЗ-11. , ,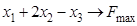

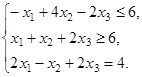ИЗ-12. ,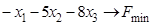

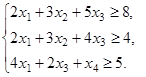
ИЗ-13. ,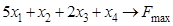

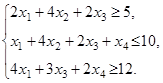
ИЗ-14. ,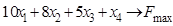

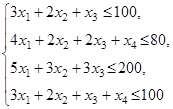
Задание 3 (варианты)

Задачи для самостоятельного решения:

Используя сначала методом дихотомии, затем метод золотого сечения и метод Фибонначи с точностью e = 0, 01 вычислить экстремум представленных функций:

1) g (x)= x ³ –cos (x)+1, вычислить минимум в интервале (–0.5, 0.5););

2) g (x)= x ² +10sin(x) – 12, вычислить максимум в интервале (1.5, 2.5);

3) g (x)=ln(x) – x ², вычислить максимум в интервале (0.0, 1.5);

4) g (x)=ln(x)+ 3cos(x), вычислить минимум в интервале (2.5, 3.5);

5) 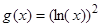, вычислить минимум в интервале (0.5, 1.5);

6) g (x)=(ln(x) – 1)sin(x)+0.88, вычислить минимум в интервале (0.5, 1.5);;

7) g (x)=3 x ² +x – cos(x²), вычислить минимум в интервале (–. 5, 0.5);

8) 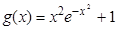, вычислить минимум в интервале (–. 5, 0.5);

9) 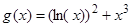в интервале (0.1, 1.0);

10) 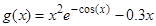, вычислить минимум в интервале (– 0.5, 0.5);;

11) g (x) = ln(x)(1 – сos(x)), вычислить минимум в интервале (0.1, 1.0);;

12) g (x) = ln(x+1)сos(x), вычислить максимум в интервале (0.0, 1.0);

13) 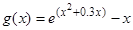, вычислить минимум в интервале (– 0.5, 0.5);

14) g (x) =x ² – x+0.3cos(x), вычислить минимум в интервале (0.0, 1.0);

15) 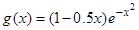, вычислить максимум в интервале в интервале (– 0.5, 0.5);;

При решении задач выбрать 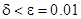.