Пример метод с переменным шагом

Найти минимум функции

,

где . Начальные условия , .

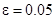Первая итерация. 1.1) Вычисляем градиент в точке :

.

1.2) Найдем новое значение 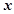после смещения из точки :

.

1.3) Проверка условия остановки: 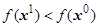. Оно не выполняется, так как , 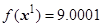. Уменьшаем шаг .

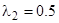1.4) Новое значение 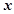после смещения из точки равно:

.

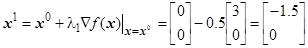1.5) Условие 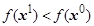не выполняется, так как , . 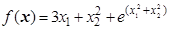Уменьшаем шаг 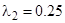. Значение 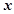после смещения из точки равно:

.

1.6) Условие 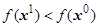выполняется, так как , .

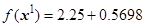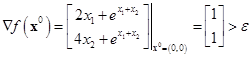Пример. метод наискорейшего спуска. Дано: Найти минимум функции .

Начальная точка 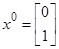, точность решения

.

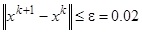Вектор градиента этой функции имеет вид:

.

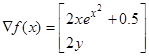Итерация 1. Вычислим градиент в точке :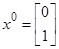

.

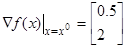Сделав шаг вдоль направления антиградиента, найдем новую точку спуска

.

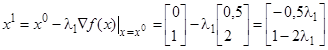Вычислим значение функции в новой точке

.

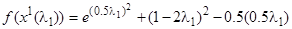Найдем такую величину шага, чтобы целевая функция достигла минимума вдоль выбранного направления. У функции 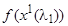имеется экстремум, если выполняется необходимое условие 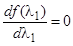. Запишем его в виде:

Откуда определим шаг: λ ₁ = 0.4981. Зная шаг, находим в явном виде новую точку:

.

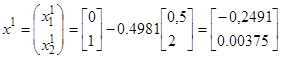Проверим критерий остановки: 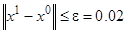. Он не выполняется:

.

Итерация 2.

Вычислим градиент в точке :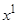

.

Сделаем шаг вдоль направления антиградиента

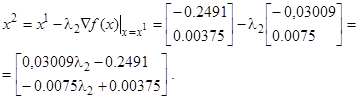
Подставив найденные координаты , 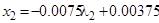в функцию , получим

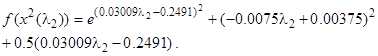
Найдем такой шаг, при котором целевая функция достигала минимума. Продифференцируем функцию по 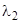и приравняем ее производную нулю ():

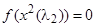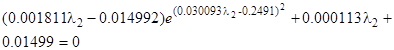
Определив корень этого уравнения, найдем шаг:

λ ₂ = 0.4256.

Координаты новой точки с этим шагом таковы:

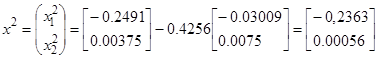
После второй итерации критерий остановки выполняется:

.

Ответ , .

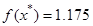Проверим решение задачи в МАТЛАБ.

[М, f] = fminsearch(@ftest2, [1.4, 0.6])

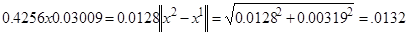
math.semestr.ru Минимум функции методом наискорейшего спуска