
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример оформления. Пример решения задачи
|
|
Строим график, чтобы убедиться, что минимум есть.

1) Используя метод дихотомии, вычислить минимум функции g (x)=ln(x)+3cos(x), в интервале (2.5, 3.5) c точностью  .
.
По формуле (10), полагая  , найдем:
, найдем:  ,
,  ,
,  ,
,  . Так как
. Так как 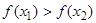 , то координаты концов нового интервала таковы:
, то координаты концов нового интервала таковы:  и
и  . Проверяем условие остановки
. Проверяем условие остановки 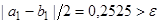 . Перейдем ко второму шагу.
. Перейдем ко второму шагу.
k= 2)  ,
, 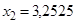 ,
,  ,
,  . Так как
. Так как  , то координаты концов нового интервала
, то координаты концов нового интервала  и
и  ,
,  . Третий шаг.
. Третий шаг.
k= 3)  ,
,  ,
,  ,
,  . Так как
. Так как  , то координаты концов нового интервала
, то координаты концов нового интервала  и
и  . Проверка условия остановки:
. Проверка условия остановки:  . Четвертый шаг.
. Четвертый шаг.
k= 4)  ,
,  ,
,  ,
,  .
.
Так как  , то координаты концов нового интервала
, то координаты концов нового интервала  и
и  . Проверка условия остановки:
. Проверка условия остановки:  . Пятый шаг.
. Пятый шаг.
k= 5)  ,
,  ,
, 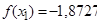 ,
,  .
.
Так как 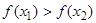 , то координаты концов нового интервала
, то координаты концов нового интервала  и
и 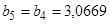 . Проверка условия остановки:
. Проверка условия остановки:  . Шестой шаг.
. Шестой шаг.
k= 6)  ,
, 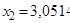 ,
,  ,
,  .
.
Так как  , то координаты концов нового интервала
, то координаты концов нового интервала  и
и  . Проверка условия остановки:
. Проверка условия остановки:  . Седьмой шаг.
. Седьмой шаг.
k= 7)  ,
,  ,
,  ,
,  . Так как
. Так как  , то координаты концов нового интервала
, то координаты концов нового интервала  и
и  . Проверка условия остановки:
. Проверка условия остановки:  . Условие остановки выполнено. Конец. Ответ:
. Условие остановки выполнено. Конец. Ответ:  ,
,  .
.
Проверим полученное решение с помощью МАТЛАБ. Предварительно нужно создать файл-функцию, ее назовем, например opt. Минимум функции g (x)=ln(x)+3cos(x) в интервале (2.5, 3.5) найдем с помощью функции fminbnd, задав первым аргументом имя файл-функции, а вторым и третьим - границы отрезка, на котором ищется локальный минимум.
> > function g = opt(x) g=ln(x)+3cos(x);
> > x2=fminbnd(@opt, 0.0, 1.0)
Задание 4 (вариант) (найти экстремум в МАТЛАБ и одним из методов см. интернет «math.semestr.ru Минимум функции методом наискорейшего спуска»)
Задачи для самостоятельного решения метод покоординатного спуска, либо градиентный метод с переменным шагом, методом Ньютона, метод наискорейшего спуска.
Найти координаты минимума функций
1) 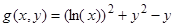 ;;
;;
2)  ;;
;;
3)  ;;
;;
4)  ;;
;;
5)  ;;
;;
6)  ;;
;;
7)  ;;
;;
8)  ;;
;;
9)  ;;
;;
10)  ;
;
11) 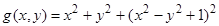 ;;
;;
12)  ;;
;;
13);  ;.
;.
14)  ;
;
15)  ;;
;;
Пример решения задачи поиска минимума функции нескольких переменных в МАТЛАБ с помощью команды fminsearch. Найти значения переменных 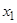 ,
,  , при которых функция
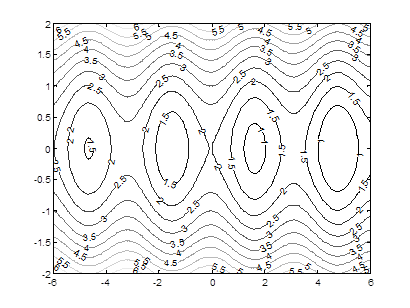
, при которых функция  достигает минимума. Проведем сначала анализ поведения этой функции, построив ее линии уровня при помощи следующих команд:
достигает минимума. Проведем сначала анализ поведения этой функции, построив ее линии уровня при помощи следующих команд:
> > [X, Y] = meshgrid( 6:.1: 6,
6:.1: 6,  3:.1: 3);
3:.1: 3);
> > Z=Y.^2+(cos(X)).^2  0.1.*X+1;
0.1.*X+1;
> > [C, h] = contour(X, Y, Z);
> > set(h, 'ShowText', 'on', 'TextStep', get(h, 'LevelStep')*2)
> > colormap (gray)
На рис. 1 изображены линии уровня, по которым можно судить, где расположены минимумы. Значение минимума можно вычислить точно, выбрав начальное приближение вблизи интересующего нас минимума. Так если выбрать начальное приближение  ,
,  , то вычисление в МАТЛАБ дает
, то вычисление в МАТЛАБ дает
> > opt=@(x)(x(2).^2+1+(cos(x(1))).^2+0.1.*x(1));
> > [x, Z]= fminsearch(opt, [  1.0, 0.0])
1.0, 0.0])
x =
 1.6209 0.0000
1.6209 0.0000
Z =
0.8404
Если же за начальное приближение возьмем  ,
,  , то эти вычисления дают:
, то эти вычисления дают:
> > [x, Z]= fminsearch(opt, [1.0, 0.0])
x =
1.5207 0.0000
Z=
1.1546
Выбирая последовательно подходящие начальные приближения, можно найти все точки минимумов и максимумов функции.
Примеры оформления