РЕШЕНИЯ 6 страница

192. Выход существует. Ведь условия соглашения касаются лишь выигрыша первого дела. Значит, если учитель подаст в суд повторно, то оговоренное условие уже не будет действовать, и он сможет получить деньги по решению суда.

193. Для быстрого устного решения задачи нужно сообразить, что сумма последовательных чисел от 1 до 100 складывается из следующей суммы пар чисел: 1-го с последним, 2-го с предпоследним и т. д. Каждая такая пара равна в сумме 101, а всего таких пар 50.

Итак, нужно просто у множить 101 на 50, что легко сделать устно: 101 х 50 = 5050.

194. 80 % от 25 % равно 20 %.

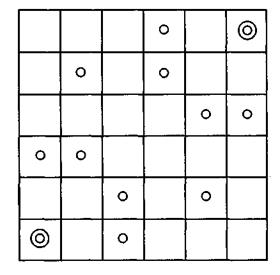
196. 12 павильонов (включая два административных).

Решение задачи ясно из рисунка.

197. Эту задачу удобно начинать решать с конца. Обозначим через х конечные капиталы каждого из партнеров. Тогда к началу третьей операции (в этом месяце) текущие капиталы партнеров А, Б, В должны были соответственно составить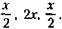

К началу второй операции (месяц назад) текущие капиталы партнеров А, Б, В соответственно составляли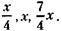

А к началу первой операции (два месяца назад) начальные капиталы партнеров А, Б, В выглядели так:

При этом потери партнера А равны:

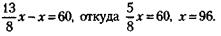
Следовательно, начальный капитал партнера А равен:

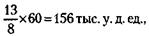
партнера Б

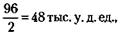
партнера В:

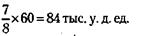
198. Обозначим через х и у вложения в операции А и Б соответственно. Тогда условие задачи можно записать так:

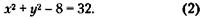
Решим систему из двух уравнений с двумя неизвестными.

Из (1) следует: у = 8 - х.

Подставляя значение у в(2), получим:

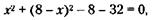
откуда

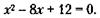
Решая квадратное уравнение по стандартной формуле, получим:

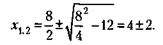
х₁ = 6 (х₂ не подходит, так как при нем х < у, что противоречит условию).

Следовательно, сумма вложения в операцию А равна 6 млн у. д. ед., в операцию Б: 8 – 6 = 2 млн у. д. ед.

199. Обозначим через х возраст сооружения Б. Тогда условие задачи можно записать так:

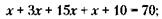
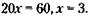
Следовательно:

возраст сооружения А – 9 лет,

возраст сооружения Б – 3 года,

возраст сооружения В – 45 лет,

возраст сооружения Г – 3 года,

возраст сооружения Д – 70 лет.

200. Обозначим через х количество дней, когда предприниматель был здоров, а через у – нездоров. Тогда условие задачи можно записать так:

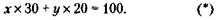
Здесь х и у – целые положительные числа.

Произведем перебор х.

При х = 1 выражение (*) будет таким:

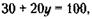
откуда

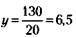
(такое дробное значение у не подходит).

При х = 2 выражение (*) будет таким:

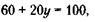
откуда

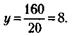
(это значение у подходит).

Итак:

1) Количество дней, когда предприниматель был здоров, равно 2, нездоров – 8.

2) Действие договора продолжалось 2 + 8 = 10 дней.

201. Интерполируя с помощью таблицы сложных процентов, получим:

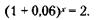
Откуда х₁ = 12 месяцев.

202. Интерполируя с помощью таблицы сложных процентов, получим:

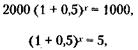
откуда х = 4 дня.

203. Прибыль торговой фирмы может составить для каждой партии товара:

при закупке партий в 1000 единиц

(100 - 80) х 1000 = 20 000 у. д. ед.;

при закупке партий в 2000 единиц

(100 - 60) х 2000 = 80 000 у. д. ед.

Если фирма располагает информацией о том, что с равной вероятностью может иметь место спрос как на 1000, так и на 2000 единиц товара, то среднеожидаемая прибыль (математическое ожидание прибыли) равна:

20 000 х 0, 5 + 80 000 х 0, 5 = 50 000 у. д. ед.

Если такая полная информация о покупательском спросе отсутствует и будет принято решение о закупке 1000 единиц товара при вероятности реализации этой партии 0, 5, то прибыль составит:

20 000 х 0, 5 = 10 000 у. д. ед.,

а при закупке 2000 единиц (при той же вероятности реализации):

80 000 х 0, 5 = 40 000 у. д. ед.

Следовательно, даже при более благоприятном варианте закупки 2000 единиц потери от неполноты информации равны:

50 000 - 40 000 = 10 000 у. д. ед.

1) Это и есть стоимость информации, т. е. та сумма, которую целесообразно израсходовать на изучение покупательского спроса.

2) Наиболее прибыльна закупка партии товара при наличии полной информации: в половине случаев следует закупать 1000 единиц товара, а в половине – 2000 единиц.

204. Обозначим вес большого арбуза через х, а стоимость одного килограмма его – через у.

При этом стоимость большого и малого арбуза будет составлять:

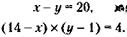
Решая полученную систему из двух уравнений с двумя неизвестными, придем к квадратному уравнению:

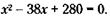
Решая уравнение по стандартной формуле, получим:

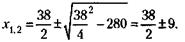
x₁ не подходит, так как общий вес покупки равен 14 кг.

Следовательно, х₂ = 10 – вес большого арбуза, а маленький арбуз весит 14-10 = 4 кг.

205. Обозначим капитал акционера А через х, а капитал акционера Б через у и составим два очевидных уравнения:

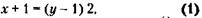
Решая совместно уравнения (1) и (2), найдем:

х = 7 млн руб., у = 5 млн руб.

206. Проще всего решить эту задачу так. Мысленно включим в раздел еще один – восемнадцатый автомобиль. Тогда договорные доли от 18 автомобилей составят:

для участника А – 9 автомобилей,

для участника Б – 6 автомобилей,

для участника В – 2 автомобиля.

В сумме это и будет 17 автомобилей. Такой раздел не совсем точен, но понятен и по-своему справедлив.

207. Возраст фирмы Б равен: 31 -8 = 23 года.

Возраст фирмы А: 23 х 2 = 46 лет.

208. Обозначив уставной фонд предприятия А через х, а уставной фонд предприятия Б через у, можем записать:

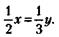
Из этого следует, что

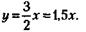
Иными словами, уставной фонд предприятия Б в полтора раза больше, чем предприятия А.

209. Обозначив через х искомое количество акционеров, составим следующее очевидное уравнение:

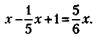
Решение этого уравнения дает искомый ответ: х = 30 человек.

210. Вначале определим, какой процент от общего числа составляют отсутствующие акционеры:

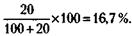
Тогда процент, который составляли присутствующие акционеры, будет равен:

100 % - 16, 7 % = 83, 3 %.

211. Обозначим уставной фонд в рублях через х, тогда доля первого участника в уставном фонде составит 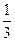х, доля второго участника - 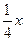, доля третьего - 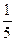х, а весь уставной фонд будет равен:

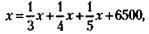
откуда следует, что х = 30 000 руб.

Доля первого участника – 10 000 руб., доля второго – 7500 руб., доля третьего – 6000 руб.

212. Если обозначить время, которое прошло, через х, то оставшееся время будет равно

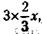
а всего в сутках

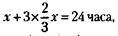
отсюда х = 8 часам (утра).

213. Обозначив возраст предприятия через х, можно записать условие задачи следующим образом:

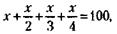
откуда следует, что х = 48 годам.

214. На все привилегированные акции дивиденд составит:

6 х 5 % = 30 % от 100 млн руб., или 30 млн руб.

На все обыкновенные акции при этом останется для выплат дивидендов

100 млн руб.– 30 млн руб. = 70 млн руб.

Таким образом, на одну обыкновенную акцию придется дивиденд, равный

70 млн руб.: 28 = 2, 5 млн руб.

На одну привилегированную акцию дивиденд равен 5 % от 100 млн руб., т. е. 5 млн руб.

215. 1) Курс акций (К_а) рассчитывается по формуле:

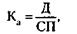
где Д – дивиденд,

СП – ссудный процент. ^;

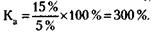
Курсовая стоимость акции 30 тыс. руб.

2) Учредительская прибыль (УП) рассчитывается по формуле:

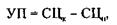
где СЦ_к и СЦ_н – суммарная цена по курсу и по номиналу соответственно.

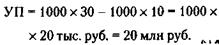
Стоимость единицы продукции равна:

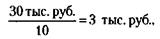
1) При росте производительности труда в три раза будет выпускаться 30 единиц продукции в день, и стоимость единицы продукции станет

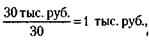
а стоимость массы продукции – 30 х 1 = 30 тыс. руб.

2) При увеличении интенсивности труда в два раза 10 единиц продукции будет производиться за полдня, а в день будет произведено 20 единиц продукции. Следовательно, стоимость единицы продукции станет

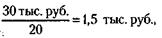
а стоимость массы продукции – 20 x 1, 5 = 30 тыс. руб.

217. 1) Норма прибыли (НП) рассчитывается по формуле:

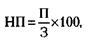
где П – прибыль, З – затраты.

С учетом того, что З = В - П, где В – величина выручки, получим:

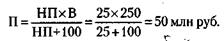
Сумма эмиссии равна:

П + 4 % П = 50 + 2 = 52 млн руб.

2) Общая стоимость привилегированных акций:

100 х 100 тыс. руб. = 10 млн руб.

При этом на обыкновенные акции остается 52 - 10 = 42 млн руб., что дает возможность выпустить

42: 0, 5 = 84 обыкновенные акции.

218. 1) Курс акций рассчитывается по формуле (см. решение задачи 215):

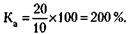
Курсовая цена акции при этом 200 тыс. руб.

2) Учредительская прибыль рассчитывается

по формуле (см. решение задачи 215):

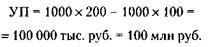
219. Если бы у партнеров было 8 общих счетов, Семенов израсходовал бы их за 12 х 8 = 96 месяцев. А Семенов и Федоров за 96 месяцев израсходовали бы деньги с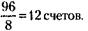

Теперь понятно, что за эти же 96 месяцев Федоров израсходовал бы деньги с 12 - 8 = 4 счетов.

Отсюда получается, что один счет Федоров

способен израсходовать за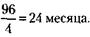

220. 1 каменщик выложит 2 м стены за 4 часа, 1 м – за 2 часа, 5 м – за 10 часов; 2 каменщика выложат 5 м стены за 5 часов.

221. Все три проекта вполне реальны. Первый проект изучается странами Аравийского полуострова. Второй проект не экономичен: на каждый подъем и спуск аэростата расходуется много энергии. Третий проект запатентован и опробуется в нашей стране.

222. 1) Прибыль рассчитывается по формулам (см. решение задачи 171):

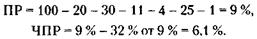
Для того чтобы 6, 1 % составили 1 млн руб., нужно получить доход (сумму выручки от реализации книги), равный

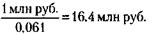
Для этого цена одной книги при тираже 100 тыс. экз. должна быть:

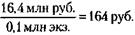
С учетом НДС: 164 + 20 % = 197 руб.

2) Авторский гонорар равен 3–5 % от 16, 4 млн руб., т. е. 492-820 тыс. руб.

3) На бумагу, картон и другие материалы будет выделено 20 % от 16, 4 млн руб., т. е. 3, 28 млн руб.

4) Типографские расходы составят 30 % от 16, 4 млн руб., т. е. 4 млн 920 тыс. руб. Издательские расходы составят 10–12 % от 16, 4 млн руб., т. е. 1 млн 640 тыс.– 1 млн 968 тыс. руб.

5) Торговым организациям придется заплатить 25 % от 16, 4 млн руб., т. е. 4 млн 100 тыс. руб.

6) Расходы на маркетинг, включая рекламу, равны 1 % от 16, 4 млн руб., т. е. 164 тыс. руб.

7) При установлении цены книги 300 руб. ее цена без учета НДС составит 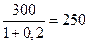руб.

Сумма выручки от реализации книги будет 250 руб. х 0, 1 млн экз. = 25 млн руб. Чистая прибыль, равная 6, 1 % от 25 млн руб., составит 1 млн 525 тыс. руб.

223. 9 часов.

224. Предположим, рассматривается экономия энергетических ресурсов, эквивалентных 100 тоннам топлива. Тогда в результате реализации первого предложения можно будет обойтись 65 тоннами топлива (100 - 35 %), после реализации второго предложения – 32, 5 тонны (65 - 50 % от 65), после реализации третьего – 27, 7 тонны (32, 5 - 15 % от 32).

Таким образом, общая экономия составит 100-27, 7 = 72, 3%.

225. Поскольку каждый должен вложить равную долю – 150 тыс. руб., то долг третьего компаньона первому составляет 230 - 150 = 80 тыс. руб., а второму – 220-150 = 70 тыс. руб.

226. Доля каждого предприятия составляет 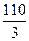блоков, которые стоят 110 тыс. у. д. ед.

Отсюда стоимость 1 блока равна:

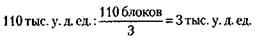
Из этого следует, что первое предприятие затратило 70 блоков по 3 тыс. у. д. ед., т. е. 210 тыс. у. д. ед.; второе – 40 блоков по той же цене, т. е. 120 тыс. у. д. ед.; третье, как известно, затратило 110 тыс. у. д. ед.

Очевидно, что третье предприятие должно первому 100 тыс. у. д. ед. (210-110) и второму 10 тыс. у. д. ед. (120-110).

227. Наливаем в соответствующую емкость ровно 8 литров вина, из которой отливаем в 5-литровую ровно 5 (при этом в 8-литровой емкости остается ровно 3 литра).

Из 5-литровой емкости вино переливаем в 12-литровую и в освободившийся сосуд наливаем оставшиеся в 8-литровой емкости 3 литра.

Снова из 12-литровой заполняем вином 8-литровую емкость, из которой заливаем доверху 5-литровую (в которой уже есть 3 литра). При этом в 8-литровой емкости остается ровно 6 литров.

228. Обозначим новый результат фермера – количество ежедневно вспахиваемой земли – через х. Тогда величина участка будет равна 8х (теперь он вспахивает его за 8 дней), и условие задачи можно записать так:

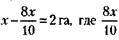– старый результат фермера.

Из этого следует, что 1) х = 10 га, 2) величина участка равна 8 х = 80 га.

229. Принимая количество автобусов, выпускаемых в день до реконструкции предприятия, можно записать условие задачи в виде следующего уравнения:

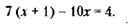
Отсюда х = 1, а количество автобусов, выпускаемых в день после реконструкции, равно х + 1 = 2.

230. Принимая количество изделий, выпускаемых в день по норме, за х, можно записать условие задачи в виде следующего уравнения:

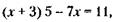
откуда х = 2.

Количество изделий, выпускаемых в день, фактически равно х + 3 = 5.

231. Принимая вес, потерянный яблоками после сушки, за х, можно записать условие задачи следующим образом:

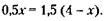
Откуда х = 3, а искомый вес 4 т яблок после сушки равен 4 - 3 = 1 т.

232. Последовательность решения задачи такова:

1) Одна корова большого стада (70 коров) могла бы питаться травой 1680 дней (24 дня х 70 коров).

2) Одна корова малого стада (30 коров) могла бы питаться травой 1800 дней (60 дней х 30 коров).

3) Следовательно, за 36 дней (60 - 24) успевает нарасти трава, достаточная для питания одной коровы в течение 120 дней (1800-1680).

4) Значит, и за последующие 36 дней (96 -60) нарастет столько же травы, сколько хватит одной корове на 120 дней.

5) А всего количество дней, в течение которых могла бы питаться травой одна корова искомого стада, составит:

1800 + 120 = 1920 дней.

6) Зная, что коровы искомого стада будут питаться травой 96 дней, нетрудно найти, сколько в этом стаде коров:

1920 дней: 96 дней = 20 коров.

233. Первоначальное количество зеленой краски обозначим через х, тогда количество желтой составит 1 - х. После добавления 1 - х зеленой и х желтой краски количество красок разных цветов уравнялось (стало равным по 1). Следовательно, по 50 % краски каждого цвета.

234. В тонне сахара при влажности 15 % содержится 150 кг воды и 850 кг сухого вещества. После просушки количество воды уменьшилось на 80 кг и стало равно 70 кг. Следовательно, теперь влажность сахара составляет:

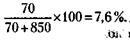
235. Вес жидкости в изделии до его сушки составлял 6 кг. Обозначая потери жидкости при сушке через х, можно записать условие задачи так:

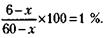
Откуда х = 5, 45 кг.

Следовательно, вес изделия после сушки равен: 60 - 5, 45 = 54, 55 кг.

236. В одной тонне переработанного сырья по условию задачи содержится 0, 17 т жидкости и 0, 83 т сухого вещества. С учетом этого обстоятельства и принимая за х вес испарившейся в процессе переработки жидкости, можно записать условие задачи так:

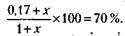
Откуда х= 1, 77 т.

Следовательно, для того чтобы получить одну тонну продукта, нужно переработать сырья 1 + 1, 77 = 2, 77 т.

237. В 100 т морской воды по условию задачи содержится 6 т соли. С учетом этого обстоятельства и принимая за х количество пресной воды, необходимое для опреснения, можно записать условие задачи так:

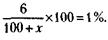
Откуда х = 500 т.

238. В слитке сплава по условию задачи содержится 4 кг золота. С учетом этого обстоятельства и принимая за х количество золота, которое нужно добавить к слитку, можно записать условие задачи так:

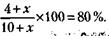
Откуда х = 20 кг.

239. Принимая первоначальный вес сахара за х, а вес сахара после просушки за x_1, можно записать условие задачи так:

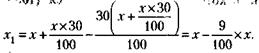
Следовательно, вес высушенного сахара стал на 9 % меньше первоначального.

240. Раньше 5 деталей из 100 были с браком, теперь 1 деталь из 100. Следовательно, брак сократился на

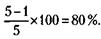
241. Примем старое количество единиц продукции, выпускаемых в единицу времени, за 1. При этом время, затрачиваемое на единицу продукции, равно 1. Новое количество единиц продукции стало 1, 5. Значит, теперь время, затрачиваемое на единицу продукции, равно 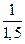= 0, 67, т. е. сократилось на 33 %.

243. Первый экскаватор проработал на 4 часа меньше нормы и в результате недоработал 40 % задания. Значит, первый экскаватор способен выполнить 100 %задания за

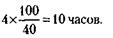
А за 8 часов первый экскаватор отработает 80 % задания.

Это означает, что второй экскаватор за 8 часов выполнил 100 - 80 = 20 % задания. А 100 %

задания второй экскаватор выполнит за

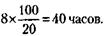
244. Принимая работу, выполненную бригадой № 1 в час, за единицу, можно записать, что обе бригады в час выполняют:

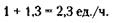
А за 10 часов обе бригады выполняют:

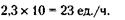
Следовательно, бригада № 1 смогла бы самостоятельно выполнить данную работу за 23: 1 = 23 часа, бригада № 2 - за 23: 1, 3 = 17, 7 часа.

245. Принимая сторону садового участка до увеличения за 1, получим его периметр, равный 4, а площадь – 1. С увеличением периметра на 20 % его стороны также вырастут на 20 % и станут равны 1, 2. Площадь при этом будет равна (1, 2)² = 1, 44, т. е. вырастет на 44 %.

246. Принимая сторону садового участка до увеличения за единицу, получим его площадь, равную единице. Площадь участка с увеличением на 40 % его сторон станет равна 1, 4 х 1, 4 = 1, 96, т. е. вырастет на 96 %.

247. Принимая сторону прямоугольного садового участка до увеличения за единицу, получим его площадь, равную единице. С изменением сторон участка его площадь станет равна 1, 3 х 0, 7 = 0, 91, т. е. уменьшится на 9 %.

248. Находим, какие доли дома строительные организации строят за один год, и суммируем эти доли:

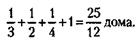
Исходя из того, что эта суммарная доля строится за 365 дней, рассчитываем (из пропорции), за сколько дней строится единица дома:

249.

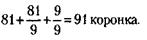
250. Поскольку копия легче натуры в 8 миллионов раз и сделана из того же металла, то ее объем должен быть меньше объема натуры тоже в 8 миллионов раз. Но объемы тел относятся, как кубы их высот. Следовательно, копия должна быть ниже натуры в

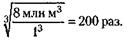
Высота Эйфелевой башни около 300 м, поэтому высота копии должна быть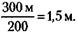

251. Поскольку объемы тел относятся, как кубы их линейных размеров, большая емкость должна быть в 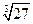= 3 раза выше и шире. Поверхности же подобных тел относятся как квадраты линейных размеров, т. е. поверхность большей емкости в З² = 9 раз больше, а значит, и в 9 раз тяжелее.

252. Объем меньшего блока будет в 5³ = 125 раз меньше.

Следовательно, он будет весить

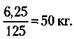
253. Обозначим через х количество спирта, который отлили в первый раз, и количество смеси, отлитой во второй раз. Тогда после первого отливания в емкости останется 100 - х спирта, а после доливания в нее воды в каждом литре смеси будет содержаться