Логические операции с суждениями

Существует ряд других способов преобразования формы суждения, полезных при логических операциях над суждениями. Формы эти:

1) обращение;

2) превращение;

3) преобразование посредством противопоставления предикату.

Обращение

Обращением называется преобразование, при котором предикат суждения становится субъектом, субъект — предикатом, но логическое содержание суждения остается то же самое.

Превращение

Второй вид преобразования формы суждений, не изменяющего содержания суждений, составляет превращение.

Превращение есть лишь преобразование формы суждения. Посредством превращения мыслится то же самое отношение между понятиями, которое мыслилось в исходной форме суждения. Но как ни мало существенно с логической точки зрения это преобразование, оно все же раскрывает с некоторой новой стороны мыслимое в исходном суждении отношение между субъектом и предикатом. И действительно, в исходной форме суждения предмет мыслится как обладающий известным свойством. В превращенной форме раскрывается, что тот же предмет не может обладать свойством или отношением, несовместимыми со свойством или отношением, которые выражаются предикатом, т. е. свойством или отношением, понятие которых противоречит понятию предиката. То же определенное свойство или отношение предмета, которые одним способом мыслились в исходной форме суждения, в превращенном суждении мыслятся уже другим способом — через отношение к противоречащему понятию.

Противопоставление предикату

Третий вид преобразования формы суждения есть противопоставление предикату. Основывается оно на том, что каждое понятие может мыслиться не только в своем собственном положительном содержании, но и по отношению к противоречащему ему понятию.

Противопоставление предикату является соединением превращения с обращением. Чтобы произвести противопоставление, сначала производится превращение, а затем превращенное суждение обращается.

Таким образом, мы обратили внимание на структуру и виды суждений. Рассмотрели основные операции, проводимые с суждениями, изучили отношения между простыми суждениями и сложными суждениями.

Тема 4. Умозаключение

Лекция 1

Умозаключение как форма мышления

Дедуктивное умозаключение и его виды

Умозаключение как форма мышления

Некоторые истины устанавливаются прямо, без всяких рассуждений, путем простого усмотрения того, что показывает наблюдение, или того, что представляется очевидным для мысли. Таковы суждения «сейчас небо пасмурно»; «эта книга стоит на полке»; «целое больше своей части” и т. д. Истинность подобных суждений не приходится доказывать, так как она очевидна.

Но очевидные утверждения составляют лишь небольшую часть всех истин. В огромном большинстве случаев истина не есть положение, прямо видное или само собой разумеющееся. Обычно для установления истины приходится произвести в каждом случае особое исследование: отчетливо поставить вопрос, принять во внимание другие, уже ранее установленные истины, собрать все необходимые для решения вопроса факты и наблюдения, поставить опыты, обдумать их результат, проверить на практике справедливость возникшей догадки и т. д.

Логическое мышление осуществляется и тогда, когда высказываются очевидные истины, и тогда, когда истины не очевидны, а добываются более сложным путем. В последнем случае логическое мышление принимает форму рассуждения. Рассуждением называется ряд суждений, которые все относятся к определенному предмету или вопросу и которые идут одно за другим таким образом, что из предшествующих суждений необходимо вытекают или следуют другие, а в результате получается ответ на поставленный вопрос, что организм состоит из клеток, что площадь треугольника равняется половине произведения основания на высоту, что Петр I был одним из величайших русских государственных деятелей, — все эти и многие другие суждения не просто провозглашаются в качестве истин, но обосновываются при помощи особых рассуждений.

Уже рассматривая суждение и различные формы преобразования суждений, мы видели, что суждение редко мыслится отдельно от других суждений. Чтобы правильно понять смысл данного суждения, нам часто приходится рассматривать не только одно это суждение, но также и другие суждения, с которыми оно связано отношением противоположности или подчинения.

Во множествах случаев мы даже не можем убедиться в истинности данного суждения до тех пор, пока мы не рассмотрим его отношения к другим суждениям. Предположим, например, что мы не знаем, какая связь существует между понятием «Иванов» и понятием «преступник». Совершил ли Иванов преступление?

До тех пор пока мы рассматриваем только отношение между понятием «Иванов» и понятием «преступление», мы не можем ответить на поставленный вопрос и, следовательно, не можем сказать, в каком отношении они находятся. Станем теперь поступать иначе. Рассмотрим, до того еще как отвечать на поставленный вопрос, два другие суждения: «все убийцы — преступники» и «Иванов — убийца». Предположим, что мы уже убедились ранее в истинности этих двух суждений. Но если нам известно, что все убийцы являются преступниками и что Иванов — убийца, то можем ли мы сказать что-нибудь об отношении понятия «Иванов» к понятию «преступник»? Очевидно, можем. Основываясь на том, что все убийцы являются преступниками и что Иванов — убийца, мы можем высказать суждение: «Иванов — преступник». Суждение это будет истинным. Но истинность этого суждения мы усмотрели не прямо. Это отношение, выраженное в суждении «Иванов — преступник», мы получили посредством умозаключения, или вывода. Связь между понятиями «Иванов» и «преступник», не видную сразу или непосредственно, мы вывели, т. е. уяснили через отношение каждого из этих понятий к некоторому третьему понятию — к понятию «убийца». Именно поэтому нам для обоснования вывода понадобились два суждения. В одном из них мы рассмотрели отношение понятия «Иванов» к понятию «убийца», в другом — отношение понятия «преступник» к тому же понятию «убийца».

То логическое действие, посредством которого обнаруживается истинность этих новых суждений, называется умозаключением. Иначе говоря, умозаключением называется форма мышления, состоящая в том, что истинность некоторого суждения выводится из истинности двух или нескольких других суждений.

Суждения, из которых можно получить вывод и из которых, раз они признаны истинными, с необходимостью следует какой-либо вывод, называются посылками или предпосылками умозаключения. В нашем примере посылками умозаключения являются суждения «все убийцы — преступники» и «Иванов — убийца».

Суждение, которое признается истинным путем умозаключения, т. е. путем сопоставления посылок, называется заключением, или выводом, в узком смысле слова. В нашем примере заключением будет суждение «Иванов — преступник».

Иногда все умозаключение в целом, т. е. все посылки и заключение вместе взятые, также называется выводом — на этот раз в широком смысле слова. Так, в нашем примере («все убийцы — преступники, Иванов — убийца, следовательно, Иванов — преступник») выводом в широком смысле слова будет все это умозаключение в целом, т. е. и его посылки, и его заключение.

Целью умозаключения является выведение новой истины из истин, нам уже ранее известных. Всякое истинное умозаключение не просто повторяет в выводе то, что нам уже известно из посылок. Истинное умозаключение ведет нашу мысль дальше того, что мы знаем из посылок, присоединяет к ранее установленным истинам истину новую. Вывод есть мысль иная сравнительно с каждой из посылок, в отдельности взятой. Вывод не есть простое повторение истин, которые мы уже мыслили в посылках. Вывод не есть и простое преобразование формы посылок, не меняющее их логического смысла, вроде обращения или превращения.

Умозаключение есть извлечение новой истины из истин, уже признанных ранее и уже известных.

Но умозаключение не просто присоединяет новую истину к истинам, уже ранее установленным или известным. Новая истина выводится из посылок таким образом, что ее присоединение к посылкам сознается нами как совершенно необходимое и обязательное для нашей мысли.

Мы можем не знать того, что все убийцы — преступники и что Иванов — преступник. Но если мы согласимся с тем, что все убийцы — преступники и что Иванов — убийца, то, соглашаясь с обеими этими посылками, уже нельзя не соглашаться с тем, что Иванов — преступник. Согласие с посылками здесь необходимо ведет к согласию с заключением. Заключение не просто присоединяется к посылкам как мысль новая сравнительно с посылками. Заключение следует из посылок как мысль, связанная с посылками необходимой логической связью.

Так как умозаключение:

1) дает в выводе мысль новую сравнительно с мыслями, выраженными в посылках;

2) раскрывает необходимость связи между посылками и выводом, то умозаключение есть очень важная форма логического мышления.

Там, где мы сразу непосредственно не видим связи между двумя понятиями, мы можем найти эту связь посредством третьего понятия, если нам только известно, в каком отношении это третье понятие стоит к каждому из наших двух понятий, связь между которыми мы стремимся выяснить. Именно эту задачу и решает умозаключение. Два понятия, отношение между которыми не видно непосредственно, умозаключение связывает посредством третьего понятия, зная отношение этого третьего понятия к каждому из них в отдельности.

Особенно важно, что связь между понятиями, раскрываемая умозаключением, есть связь необходимая. Если посылки истинны и если в ходе умозаключения мы не сделали никакой логической ошибки, то вывод всегда будет необходимо истинным. Умозаключение раскрывает не такую связь между посылкам и выводом, которая может быть истинной, но может и не быть истинной. Умозаключение раскрывает необходимость связи, существующей между посылками и выводом. Кто убедился в истинности посылок, тот должен согласиться, тот не может не согласиться с истинностью вывода.

Это свойство умозаключений — логическая необходимость всякого правильного вывода, полученного из истинных посылок, — делает умозаключение важным звеном в доказательстве и в опровержении, во всякого рода спорах и дискуссиях. Умозаключение — могучее средство убеждения. Так, получив в беседе или в споре согласие противника с посылками, мы легко можем заставить его согласиться и с выводом, как только мы покажем, что принятые им посылки необходимо вынуждают к согласию также и с выводом. Рассматривая ранее доказанные теоремы как посылки умозаключения, мы можем показать, что новая теорема, которую мы взялись доказать, есть не что иное как вывод, необходимо вытекающий из истинности этих посылок, и т. д.

Ввиду важности умозаключения для логического мышления логика систематически рассматривает все формы умозаключений. Логика исследует, какие существуют виды умозаключений, какую ценность представляет каждый из них для знания, каково строение каждой формы умозаключения, согласно каким логическим правилам делаем мы умозаключения и какие логические ошибки возможны в умозаключениях.

Дедуктивное умозаключение и его виды

Простой категорический силлогизм

Цель силлогизма, как и всякого другого умозаключения, состоит в получении из посылок нового суждения, или вывода. При этом мыслимое в выводе отношение между субъектом и предикатом вывода устанавливается не прямо. Отношение это не видно непосредственно ни из первой, ни из второй посылки, отдельно взятых. Отношение это выясняется для мысли только после сопоставления обеих посылок силлогизма. Сопоставляя посылки, мы рассматриваем отношение субъекта и предиката вывода к некоторому третьему понятию. Только через отношение итого третьего понятия к субъекту вывода и к предикату вывода выясняется отношение между субъектом и предикатом вывода.

Для удобства анализа обозначим все составные части силлогизма особыми знаками. С этой целью запишем силлогизм, расположив одну посылку под другой, а заключение, или вывод, — под второй посылкой. Отделим заключение от посылок горизонтальной чертой.

Пример силлогизма:

Все адвокаты — юристы.

Все юристы — люди.

–––––––––––––––––––––

Все адвокаты — люди.

Рассмотрим сначала заключение, или вывод. В нем понятие предиката обозначим буквой Р, понятие субъекта — буквой S. Очевидно, объем предиката в выводе больше объема субъекта (объем понятия «люди» больше объема понятия «юристы»).

На этом основании предикат вывода (Р) называется большим понятием, или большим термином силлогизма, а субъект вывода (S) — меньшим термином. Та посылка, в которую входит больший термин (Р), называется большей посылкой силлогизма. В нашем примере больший термин — понятие «люди», меньший термин — понятие «адвокаты», большая посылка — суждение «все юристы — люди». Та посылка, в которую входит меньший термин (S), называется меньшей посылкой силлогизма. В нашем примере меньшая посылка — суждение «все адвокаты — юристы».

Вывод «все адвокаты — люди» действительно обоснован данными посылками. Как же обоснован этот вывод? В меньшей посылке мы установили отношение меньшего термина к некоторому третьему понятию — к понятию «юристы». Меньшая посылка установила, что «все адвокаты — юристы», т. е. что весь объем понятия «адвокаты» полностью входит в объем понятия «юристы». В большей посылке мы установили отношение этого же самого третьего понятия к большему термину — к понятию «люди». Большая посылка установила, что «все юристы — люди», т. е. что весь объем понятия «юристы» полностью входит в объем понятия «люди». В результате оказалось возможным установить — через третье понятие (понятие «юристы») — связь между понятием «адвокаты» и понятием «люди».

Третье понятие, посредством которого в выводе выясняется отношение между меньшим и большим терминами, называется средним термином силлогизма.

Как видно из примера, средний термин входит в каждую из посылок, но не входит в заключение, или в вывод, силлогизма. Нетрудно понять, почему это так. Цель силлогизма, как мы знаем, состоит в выяснении отношения между двумя понятиями — S и Р. Средний термин появляется в силлогизме не потому, что средний термин нас интересует сам по себе. Он появляется потому, что только через отношение среднего термина к S и Р может быть выяснено не видное непосредственно отношение между S и Р. Но выяснение отношения среднего термина к S и Р достигается уже в посылках силлогизма: большая посылка раскрывает отношение среднего термина к Р, меньшая — к S. Как только задача выяснения этих отношений выполнена, как только отношение между S и Р стало ясным из отношения каждого из них в отдельности к среднему термину, средний термин перестает быть предметом нашей мысли. Наша мысль направляется уже не на средний термин, а на то отношение между S и Р, которое было выяснено с помощью среднего термина. Поэтому в выводе, или в заключении, силлогизма выступают только S и Р.

Обозначим средний термин буквой М. Тогда наш силлогизм может быть представлен следующей схемой, или, как говорят в логике, «фигурой»:

М — Р S — М

S — М или М — Р

S — Р S — Р

Как видно из примера и из его схемы, порядок посылок никакой роли не играет: большая посылка может быть первой, а меньшая — второй, и наоборот. От порядка посылок в силлогизме вывод, т. е. логическая связь между субъектом и предикатом, не зависит.

Обстоятельство это необходимо запомнить, чтобы не связывать названия «большая посылка» и «меньшая посылка» с тем порядком, в каком посылки следуют одна за другой. Независимо от этого порядка большей будет только та посылка, в которую входит больший термин, т. е. предикат вывода (Р), а меньшей — только та, в которую входит меньший термин, т. е. субъект вывода (S).

Силлогизмы могут иметь различное строение посылок, и потому самые выводы в них могут стоять в зависимости от различных правил. Логика устанавливает все эти правила и изучает все разновидности силлогизмов.

Первая группа силлогизмов — так называемые простые категорические силлогизмы. Так называются силлогизмы, в которых вывод получается из двух посылок и в которых обе посылки суть суждения категорические.

Рассматривая встречающиеся в практике мышления простые категорические силлогизмы, можно заметить, что расположение понятий, или терминов, в посылках этих силлогизмов может быть различным.

Рассмотрим следующий силлогизм:

Все адвокаты — юристы М — Р.

Иванов — адвокат S — М.

–––––––––––––––––––––––––––

Иванов — юрист S — Р.

В нем средний термин в большей посылке является субъектом, а в меньшей — предикатом.

Силлогизм, в котором понятия, или термины, расположены таким образом, называется силлогизмом первой фигуры.

Рассмотрим теперь другой пример силлогизма.

Все звезды светят собственным светом.

Ни одна планета не светит собственным светом.

–––––––––––––––––––––––––––––––––––––––

Ни одна планета не есть звезда.

Вывод — это силлогизм. В нем заключение («ни одна планета не есть звезда») получено из двух посылок. В посылках этих устанавливается отношение субъекта вывода («планета») и предиката вывода («звезда») к третьему, или среднему, понятию («тело, светящее собственным светом»). Именно через отношение среднего понятия к понятиям «планета» и «звезда» выясняется отношение этих последних между собой.

Действительно: большая посылка («все звезды светят собственным светом») устанавливает, что весь объем класса входит в объем класса М.

Меньшая посылка («ни одна планета не светит собственным светом») устанавливает, что класс S не принадлежит к классу М, т. е. что весь объем класса S целиком находится вне объема класса М.

Сопоставляя эти отношения понятий, выяснившиеся из посылок, заключаем в выводе («ни одна планета не есть звезда»), что класс S не принадлежит к классу Р, т. е. что весь объем класса S находится вне всего объема класса Р.

Присматриваясь к расположению терминов в посылках и в выводе этого силлогизма, замечаем, что это расположение.

Р — М

S — M

S — Р

отличается от расположения терминов в силлогизме первой фигуры, а именно: во втором силлогизме средний термин в обеих посылках — большей и меньшей — является предикатом. Силлогизм с таким расположением терминов называется силлогизмом второй фигуры.

Рассмотрим третий пример силлогизма.

Все студенты учатся в вузах.

Все студенты — люди.

––––––––––––––––––––––––––

Некоторые люди учатся в вузах.

И этот вывод — силлогизм. В нем на основе устанавливаемого в двух посылках отношения понятия «люди» и понятия «учащиеся в вузе» к третьему понятию («студенты») устанавливается отношение субъекта к предикату в заключении.

В третьем силлогизме средний термин в этих посылках оказывается субъектом. Силлогизм с таким расположением терминов называется силлогизмом «третьей фигуры».

Различия между тремя фигурами простого категорического силлогизма представляют интерес не только потому, что термины в посылках этих силлогизмов размещены различным образом. Различное расположение терминов в посылках связано с различным отношением между содержанием и объемом понятий, входящих в посылки и в выводы. И действительно: от того, будет ли, например, средний термин субъектом посылки или ее предикатом, зависит распределенность среднего термина в посылках, т. е. возможность мыслить средний термин во всем объеме или только в части его объема. То же справедливо и относительно большего и меньшего термина. В свою очередь от отношения между содержанием и объемом понятий, входящих в посылки и в выводы, зависит различная ценность фигур силлогизма для логического мышления и знания, а потому различная роль, какую каждая из фигур играет в доказательствах и рассуждениях.

Чтобы выяснить роль каждой фигуры, т. е. характер выводов, которые могут быть получены посредством этой фигуры, необходимо познакомиться с разновидностями фигур, или модусами.

Сравнивая различные выводы, сделанные по одной и той же фигуре, замечаем, что силлогизмы одной и той же фигуры могут различаться между собой качеством и количеством посылок и вывода.

Сравним два силлогизма.

Все люди должны учиться. Ни один человек не есть птица.

Все студенты — люди. Все юноши — люди.

–––––––––––––––––––––––– ––––––––––––––––––––––––––

Все студенты должны учиться. Ни один юноша не есть птица.

Оба эти силлогизма — силлогизмы первой фигуры, так как в обоих средний термин является субъектом в большей и предикатом в меньшей посылке. Но в то же время между этими двумя силлогизмами первой фигуры имеется и различие. Состоит оно в различном качестве посылок и вывода. В первом силлогизме обе посылки и вывод — суждения общеутвердительные. Схема этого силлогизма:

А

А

–––––

А

Во втором силлогизме большая посылка есть суждение общеотрицательное, меньшая — общеутвердительное, вывод — суждение общеотрицательное. Схема этого силлогизма:

Е

А

–––––

Е

Сравним еще два силлогизма.

Все грибы — споровые растения.

Некоторые бесцветковые — грибы.

–––––––––––––––––––––––––––––––––––––––

Некоторые бесцветковые — споровые растения.

Ни одна планета не есть звезда.

Некоторые светила — планеты.

––––––––––––––––––––––––––

Некоторые светила — не звезды.

Оба эти силлогизма — также силлогизмы первой фигуры, так как в обоих средний термин является субъектом в большей и предикатом в меньшей посылке. Но в то же время между этими двумя силлогизмами первой фигуры имеется и различие. Состоит оно в различном качестве и количестве посылок и вывода. В первом силлогизме и посылки, и вывод по качеству — суждения утвердительные. По количеству же большая посылка — суждение общее, меньшая — частное, вывод — также частное. Схема этого силлогизма:

A

I

––––

I

Во втором силлогизме большая посылка есть суждение общеотрицательное, меньшая — частноутвердительное, вывод — суждение частноотрицательное. Схема этого силлогизма:

Е

I

––––

О

Сравнивая качество и количество выводов во всех четырех примерах силлогизма первой фигуры, приведенных выше, видим, что в первом примере вывод — общеутвердительный, во втором — общеотрицательный, в третьем — частноутвердительный, в четвертом — частноотрицательный.

Разновидности силлогизмов одной и той же фигуры, обусловленные различным качеством и количеством посылок и выводов, называются модусами (от латинского слова «modus», означающего «способ», «вид»).

Итак, среди выводов простого категорического силлогизма могут встретиться выводы всех возможных видов качества и количества: А, Е, I и О. Но мы уже знаем, что различные по качеству и по количеству суждения имеют различное применение в знании и различную ценность для знания. Поэтому при изучении силлогизмов всех трех фигур большой интерес представляет вопрос, какие именно модусы может дать каждая фигура силлогизма, иначе говоря, какими могут быть выводы этой фигуры по качеству и по количеству.

Для ответа на этот вопрос необходимо прежде всего исследовать, все ли теоретически возможные модусы, т. е. все ли сочетания посылок, отличающиеся только качеством и количеством, способны давать правильные выводы. Исследование показывает, что не всякий теоретически возможный модус, т. е. не всякое сочетание качества и количества в посылках силлогизма, дает правильный вывод.

Рассмотрим, например, следующие суждения.

Все студенты обязаны держать экзамены.

Все аспиранты не являются студентами.

В этих суждениях налицо три понятия, расположенные по схеме первой фигуры простого категорического силлогизма. Термин «студенты» в одной из посылок является субъектом, в другой — предикатом. В одной посылке устанавливается отношение термина «студенты» к одному понятию, в другой — отношение того же термина к другому понятию.

Итак, расположение терминов в суждениях как будто в точности соответствует схеме первой фигуры:

М — Р

S — М

Первое суждение будет общеутвердительное, второе — общеотрицательное. Схематически количество и качество этих суждений будет следующее:

А

Е

Но, хотя расположение терминов в этом случае как будто отвечает условиям первой фигуры, правильный вывод из этих двух посылок невозможен. Из того, что «все студенты обязаны держать экзамены», и из того, что «все аспиранты — не студенты», никак нельзя вывести в качестве необходимого заключения, что, например, «аспиранты не обязаны держать экзамены». Хотя первая посылка выясняет отношение «студентов» к «лицам, обязанным держать экзамены», а вторая — отношение «студентов» к «аспирантам» — отношения эти не таковы, чтобы из них видно было, каким должно быть отношение «аспирантов» к «лицам, обязанным держать экзамены».

Итак, некоторые модусы, например модус А Е первой фигуры силлогизма, невозможны. Это значит, что качество и количество посылок в этих модусах не дают основания для правильного логического вывода. Поэтому для ответа на вопрос, какие модусы дает каждая из трех фигур простого категорического силлогизма, необходимо прежде всего выяснить условия или правила, которым должны удовлетворять посылки и входящие в эти посылки термины, чтобы вывод оказался действительно возможным. При этом оказывается, что существуют правила, общие для всех фигур силлогизма. Во всяком простом категорическом силлогизме, какова бы ни была его фигура, каков бы ни был модус этой фигуры, должны выполняться все общие для всех силлогизмов правила. Нарушение хотя бы одного из них делает умозаключение ошибочным.

Кроме правил, общих для всех фигур силлогизма, существуют и такие правила, которые являются особыми правилами для каждой фигуры силлогизма в отдельности. Правила эти обязательны для всех модусов данной фигуры силлогизма и не обязательны для модусов других фигур.

Существуют десять правил, общих для всех фигур простого категорического силлогизма. Из этих десяти общих правил два определяют число терминов и число суждений, входящих в состав силлогизма. Два других правила определяют необходимые условия распределенности терминов в посылках и в выводах силлогизма. Остальные общие правила определяют необходимую связь между качеством и количеством посылок и качеством и количеством заключений силлогизма.

Правила, определяющие число терминов и число суждений в силлогизме

Первое из общих правил состоит в том, что терминов в силлогизме должно быть три — не больше и не меньше.

Если терминов только два, то вывод не может дать ничего нового и сведется к простому повторению одной из посылок. Если терминов четыре, то вывод невозможен, так как в одной из посылок устанавливается отношение субъекта к одному термину, а в другой — отношение предиката к другому термину. Здесь нет посредствующего термина, через который могло бы быть установлено отношение или связь между субъектом и предикатом в выводе. Например, в посылках «все законы публикуются в официальных изданиях» и «всемирное тяготение — закон» понятие о публикации в официальных изданиях поставлено в отношение к понятию закона в смысле политическом, а понятие всемирного тяготения — в отношение к понятию закона природы. Так как слово «закон» обозначает здесь два различных понятия, то в наших посылках оказалось не три, а четыре термина, термин субъекта («всемирное тяготение») оказался никак не связанным с термином предиката («публикация в официальных изданиях»), и вывод, т. е. суждение, которое устанавливало бы связь между понятиями «всемирное тяготение» и «публикация в официальных изданиях», оказался невозможным.

Второе общее правило формулируется так: в силлогизме не может быть меньше и не может быть больше трех суждений. Правило это вытекает из самой сущности силлогизма. Как мы уже знаем, целью силлогизма является выяснение отношения между двумя понятиями из уже известного отношения каждого из них в отдельности к одному и тому же третьему понятию.

Отсюда видно, во-первых, что в силлогизме должно быть не меньше трех суждений. И действительно, в одном из них (меньшая посылка) раскрывается отношение понятия S к посредствующему третьему понятию М. В другом (большая посылка) раскрывается отношение другого понятия — Р к тому же посредствующему третьему понятию М. Наконец, в третьем суждении (заключение силлогизма) выясняется, какое отношение понятия S к понятию Р необходимо следует из уже раскрытого в посылках отношения каждого из них в отдельности к М.

Правда, во многих случаях может показаться, будто силлогизм состоит не из трех, но всего лишь из двух и даже из одного суждения. Так, в умозаключении «студенты, как все учащиеся, обязаны сдавать экзамены» силлогизм выражен посредством одного сложного предложения. Таких примеров можно было бы привести множество.

Однако во всех этих и подобных им случаях нас вводит в заблуждение грамматическая форма высказывания. Мы уже знаем, что грамматические формы предложения далеко не всегда совпадают с логическими формами мышления. То же имеет место и в наших примерах. В действительности силлогизм и в этих примерах состоит из трех суждений. Однако часть этих суждений — в силу быстроты мышления или стремления к краткости и сжатости выражения — только подразумевается, остается невысказанной в форме трех раздельных предложений, выражающих три раздельные суждения.

Правила распределенности терминов в посылках и выводах силлогизма

Третье общее правило формулируется так: чтобы вывод был возможен, средний термин (М) должен быть распределен по крайней мере в одной из посылок.

Так, из посылок «некоторые млекопитающие — водные животные», «все тюлени — млекопитающие».

нельзя сделать никакого вывода об отношении тюленей к водным животным. В самом деле, средний термин здесь — понятие «млекопитающие». Термин этот не распределен ни в большей, ни в меньшей посылке, т. е. имеется в виду в этих посылках не во всем своем объеме. В большей посылке он не распределен, так как является предикатом утвердительного суждения, в меньшей — так как является субъектом частного суждения.

Так как средний термин в обеих посылках не распределен, то в каждой посылке имеется в виду какая-то неопределенная точно часть его объема. При таком положении вполне возможно, что в одной посылке речь идет о какой-то одной, а в другой посылке — о какой-то другой части объема среднего термина.

Четвертое общее правило формулируется так: если больший или меньший термины не распределены в посылках, они не могут оказаться распределенными в заключении. Так, из посылок «все великие поэты обладают сильным воображением», «все великие поэты — впечатлительные люди» нельзя вывести, будто «все впечатлительные люди обладают сильным воображением». Здесь правильным будет только частный вывод: «некоторые впечатлительные люди обладают сильным воображением».

Другой пример: из посылок «все студенты должны держать экзамены» и «аспиранты не являются студентами» нельзя сделать вывод, будто «аспиранты не должны держать экзаменов». В самом деле, в выводе «аспиранты не должны держать экзаменов» больший термин как предикат отрицательного суждения был бы распределен. Но в большей посылке — «все студенты должны держать экзамены» — больший термин как предикат утвердительного суждения не распределен. Понятно, что, не будучи распределен в посылке, он не может оказаться распределенным в заключении.

Правила, определяющие связь между качеством и количеством посылок и выводов силлогизма

Пятое общее правило формулируется так: если обе посылки отрицательны, то из них нельзя получить никакого вывода. Так, из посылок «киты не есть рыбы» и «дельфины не есть рыбы» нельзя сделать никакого вывода об отношении дельфинов к китам. И действительно, обе посылки здесь — отрицательные. Из них видно, что весь объем большего и весь объем меньшего термина вне всего объема среднего термина: ни один кит и ни один дельфин не входят в число рыб.

Шестое общее правило формулируется так: если вывод из данных посылок вообще возможен и если одна из посылок при этом отрицательная, то вывод также будет отрицательным.

Рассмотрим силлогизм.

Ни один человек не есть растение.

Пшеница — злак.

––––––––––––––––––––––––––––

Пшеница не есть человек.

Здесь одна из посылок — отрицательная, а другая — утвердительная. Это значит, что объем одного из терминов, входящих в вывод, стоит вне объема среднего термина, а объем другого термина, входящего в вывод, составляет часть объема среднего термина.

Седьмое общее правило силлогизма формулируется так: из двух утвердительных посылок никогда нельзя получить отрицательного вывода. И действительно, отрицательный вывод получается при таком отношении между субъектом и предикатом вывода, когда весь объем предиката (Р) находится вне всего объема субъекта (S) или по крайней мере вне какой-то части объема субъекта. Для этого в свою очередь необходимо, чтобы весь объем Р оказался находящимся вне всего объема среднего термина (М).

Восьмое общее правило силлогизма формулируется так: из двух частных посылок ни по какой фигуре силлогизма нельзя получить правильного вывода. И действительно, если обе посылки частноутвердительные (I, I), то это значит, что в них не распределен ни один термин. Так, в посылках «некоторые преступники — убийцы» и «некоторые люди — преступники» ни один термин не распределен. Термины субъекта не распределены как субъекты в частных суждениях, термины предиката не распределены как предикаты утвердительных суждений, выражающих подчинение понятий. Так как средний термин должен быть распределен по крайней мере в одной из посылок и так как при двух частных посылках условие это не может быть выполнено, то вывод из двух частных посылок невозможен.

Девятое общее правило формулируется так: если одна из посылок частная и если вывод вообще возможен, то он может быть только частным. Если обе посылки утвердительные и одна из них общая, а другая — частная (А, I), то один термин — субъект общеутвердительной посылки — будет распределен. Но чтобы вывод получился общий, необходимо, чтобы в посылках были распределены два термина: средний, как во всех силлогизмах, и меньший, так как меньший термин не может быть распределен в выводе, если он не распределен в посылке. Но так как в нашем случае в посылках распределен всего лишь один термин, то вывод возможен только частный. Так, из посылок «все рыбы — позвоночные животные» и «некоторые водные животные — рыбы» можно получить только частный вывод: «некоторые водные животные суть позвоночные животные».

Если же из двух посылок одна утвердительная, а другая отрицательная, причем одна из них частная (IЕ, ЕI, ОА, АО), то в посылках будут распределены два термина: субъект общего суждения и предикат отрицательного. Однако и в этом случае вывод не может быть общим. И действительно, при одной отрицательной посылке вывод может получиться только отрицательный. Так как наши посылки — I Е, Е I, ОА, АО, то вывод из них может быть лишь отрицательный. Таким образом, наш общий вывод в случае если бы он был возможен, должен был бы быть отрицательным. Но так как в общеотрицательном выводе распределены и субъект, и предикат (субъект как субъект общего, предикат как предикат отрицательного суждения), то они должны быть распределены и в посылках. Кроме того, в одной из посылок должен быть распределен также и средний термин. Итак, для того чтобы вывод из наших посылок мог оказаться общим, в посылках должны быть распределены целых три термина. А так как в наших посылках распределены только два термина, то общий вывод из них невозможен.

Десятое правило, общее для всех фигур силлогизма, формулируется так: если большая посылка — частная, а меньшая — отрицательная, то вывод невозможен.

Изложенные десять правил не должны быть нарушаемы ни в одном силлогизме, какова бы ни была его фигура, каков бы ни был модус его фигуры. Всякое нарушение их уничтожает возможность вывода, ведет к логически ошибочному выводу.

Именно эта обязательность всех рассмотренных правил для каждого силлогизма объясняет нам, почему некоторые модусы невозможны, т. е. почему при некоторых сочетаниях качества и количества посылок невозможны правильные выводы. Невозможны все те модусы, в которых качество и количество посылок таково, что при этом качестве и количестве по крайней мере одно из правил силлогизма окажется нарушенным.

Но этого мало. Кроме модусов, которые должны быть исключены как не соответствующие правилам, общим для всех фигур силлогизма, исключению подлежат также и все те модусы, которые не соответствуют особым правилам каждой фигуры в отдельности. Поэтому необходимо рассмотреть и эти правила.

Специальные правила каждой фигуры все могут быть выведены из основных правил силлогизма. Но эти же правила могут быть выведены из характера выводов, которые получаются по каждой из фигур силлогизма, т. е. из характера задач, для решения которых применяется каждая фигура.

Первая фигура и ее особые правила

Первое из этих правил состоит в том, что меньшая посылка должна быть суждением утвердительным.

Итак, при отрицательной меньшей посылке вывод по первой фигуре невозможен.

Второе специальное правило первой фигуры состоит в том, что большая посылка должна быть суждением общим.

Правило это необходимо, так как в случае его нарушения большая посылка не могла бы выражать тот общий закон, в применении которого состоят выводы первой фигуры.

Теперь легко установить, какие модусы способны дать правильный вывод по первой фигуре. Для этого исключим из числа всех арифметически возможных модусов, во-первых, те, по которым вывод невозможен в силу правил, общих для всех фигур, и, во-вторых, те, по которым вывод невозможен в силу особых правил первой фигуры. После этого исключения, очевидно, останутся только правильные модусы первой фигуры: АА, ЕА, АI, ЕI, — в которых количество и качество посылок не противоречат ни общим, ни специальным для первой фигуры правилам силлогизма.

Вторая фигура и ее особые правила

Перейдем к рассмотрению второй фигуры простого категорического силлогизма.

Согласно первому из них большая посылка должна быть суждением общим.

Согласно второму специальному для второй фигуры правилу одна из посылок должна быть отрицательной.

Особенность второй фигуры состоит, во-первых, в том, что по второй фигуре невозможны никакие другие выводы, кроме отрицательных. Во-вторых, во всех без исключения модусах второй фигуры задачей вывода является именно доказательство несовместимости существенных признаков понятий S и Р, а следовательно раздельности объемов этих понятий. Здесь (разумеется, если вывод обоснован) не может быть и речи об утвердительном результате: вывод может быть только отрицательный.

Все возможные правильные модусы второй фигуры устанавливаются тем же способом, что и модусы первой фигуры. Исключив из шестнадцати арифметически возможных модусов все модусы, противоречащие общим правилам всех фигур и особым правилам второй фигуры, получаем четыре правильных модуса второй фигуры: ЕА, АЕ, ЕI, АО.

Третья фигура и ее особые правила

Выводы по третьей фигуре применяются всюду там, где предметом нашего интереса является познание частного.

Правило гласит: меньшая посылка должна быть утвердительной.

И действительно, если бы меньшая посылка третьей фигуры была отрицательной, то вывод также должен был бы быть отрицательным. Но это значит, что больший термин как сказуемое отрицательного суждения должен бы быть распределен в выводе. Однако, чтобы быть распределенным в выводе, больший термин должен быть распределен в большей посылке. Так как мы предположили, что меньшая посылка отрицательная, то большая должна быть утвердительной. Но так как в третьей фигуре больший термин — предикат, то как предикат утвердительного суждения, выражающего подчинение понятия S понятию Р, он не может быть распределен, и, стало быть, вывод по третьей фигуре в случае отрицательности меньшей посылки невозможен.

Исключив все модусы, противоречащие общим правилам всех фигур и специальному правилу третьей, получаем шесть модусов третьей фигуры: АА, ЕА, IА, АI, ОА, ЕI.

То, что заключение силлогизма третьей фигуры может быть только частным суждением, ни в какой мере не противоречит тому, что вывод третьей фигуры есть в сущности вывод о группе предметов в целом. Частный характер этих выводов показывает только то, что возможность отнесения предиката заключения к целой группе ограничена какой-то, точно не определенной частью группы.

Четвертая фигура и ее особые правила

Рассмотренные четырнадцать правильных модусов были установлены основателем науки логики древнегреческим философом Аристотелем. Уже ближайшие продолжатели логических работ Аристотеля обратили внимание на то, что в первой фигуре, кроме указанных Аристотелем четырех модусов, возможны еще пять. Модусы эти возможны в случае, если средний термин является предикатом в большей посылке и субъектом — в меньшей. (В аристотелевской первой фигуре средний термин является, напротив, субъектом в большей посылке и предикатом — в меньшей).

Спустя 500 лет после Аристотеля ученый Гален выделил правильные модусы, получающиеся при таком расположении терминов, в новую — четвертую — фигуру.

Схема четвертой фигуры:

Р — М

М — S

———

S — Р

Хотя четвертая фигура теоретически возможна и дает пять правильных модусов, в действительном мышлении выводы по четвертой фигуре не встречаются. Искусственность четвертой фигуры состоит в том, что положение меньшего и большего терминов в выводе обратно положению этих терминов в посылках. Поэтому нельзя придумать ни одного примера вывода по четвертой фигуре, который не был бы искусственным. Например:

Все тюлени — ластоногие.

Ни одно ластоногое не есть рыба.

———————————————

Ни одна рыба не есть тюлень.

Здесь естественным был бы, конечно, вывод по первой фигуре:

Ни одно ластоногое не есть рыба.

Все тюлени — ластоногие.

———————————————

Ни один тюлень не есть рыба.

Ввиду совершенной искусственности четвертой фигуры отметим только важнейшие ее особенности.

Выводы по четвертой фигуре могут быть частноутвердительные, общеотрицательные и частноотрицательные. Общеутвердительных выводов четвертая фигура (так же, как вторая и третья) не дает. Общий вывод по четвертой фигуре может быть только отрицательный. При утвердительности большей посылки меньшая посылка в четвертой фигуре должна быть общей. При отрицательности одной из посылок большая посылка в четвертой фигуре должна быть общей.

Правильные модусы четвертой фигуры: ААI, АЕЕ, IАI, ЕАО, ЕIO.

Таким образом, учитывая возможность добавочных пяти модусов четвертой фигуры, получаем всего девятнадцать правильных модусов простого категорического силлогизма.

Аксиома силлогизма и две ее формулы

Во всех силлогистических выводах есть общее им всем основание, в силу которого, признав истинными посылки, мы необходимо должны признать истинными и вытекающие из них выводы. Это общее всем силлогизмам основание выражается в следующей формуле: признак признака некоторой вещи есть признак самой вещи; то, что противоречит признаку некоторой вещи, противоречит самой вещи. Формула эта выражает в наиболее общем виде логическую связь понятий S, М и Р, на которой основывается вывод и которая делает этот вывод необходимым. Она называется аксиомой силлогизма и выражает сущность силлогизма.

Все изложенные выше правила силлогизма, относящиеся к числу терминов силлогизма, к качеству и количеству посылок, к качеству и количеству заключения, представляют не что иное как различные применения аксиомы. Аксиома силлогизма в рассмотренной нами ее форме выражает то значение, которое имеет для мышления содержание наших понятий. Но так как связью между понятиями по их содержанию определяется также и отношение между их объемами, то аксиома силлогизма может быть выражена и в другой форме, выдвигающей на первый план отношения между объемами понятий, входящих в посылки и в заключение силлогизма. В этой форме аксиома силлогизма формулируется так: «Все, что утверждается относительно целого рода или вида, должно утверждаться и относительно всего подчиненного этому роду или виду, и все, что отрицается относительно целого рода или вида, должно отрицаться относительно всего подчиненного этому роду или виду».

Каждая из приведенных двух формулировок есть выражение аксиомы силлогизма. Первая раскрывает необходимое отношение между содержанием понятий, составляющих посылки, и содержанием понятий, составляющих вывод. Вторая раскрывает необходимое отношение между объемами тех же понятий.

Условия истинности силлогистических выводов

До сих пор, рассматривая силлогистические выводы, мы всегда предполагали, что посылки, на основе которых делается вывод, истинны. Если данные посылки истинны, рассуждали мы, и если отношения между понятиями в этих посылках соответствуют условиям правильных выводов, то должны быть истинны и сами выводы.

В практике мышления это условие далеко не всегда выполняется. Далеко не всегда посылки, из которых делают вывод, являются действительно истинными.

Если одна из посылок или обе ложны, то, даже в точности выполнив все правила вывода, определяемые его фигурой, модусом, условиями распределенности терминов в посылках и так далее, мы, вообще говоря, не можем получить правильный вывод.

Рассмотрим следующий вывод.

Все растения содержат хлорофилл.

Все грибы — растения.

———————————————

Все грибы содержат хлорофилл.

Делая этот вывод, мы, очевидно, полагаем, что обе посылки истинны. Если бы они действительно были обе истинны, то, так как мы не нарушили при выводе ни одного общего и ни одного специального правила фигур силлогизма, наше заключение в выводе также было бы истинным.

В действительности, однако, большая посылка ложна по существу своего содержания. Хлорофилл имеют не все растения. Это значит, что в большей посылке мы мыслили не то отношение между содержанием понятий, а, следовательно, и не то отношение между объемами понятий, которое существует в действительности, В действительности только часть растений имеет существенные признаки растений, обладающих хлорофиллом, и потому только часть растений входит в разряд растений, имеющих хлорофилл. Истину выражала бы посылка «некоторые растения имеют хлорофилл». Соединив ее с другой истинной посылкой «все грибы — растения», мы получили бы систему посылок: «некоторые растения содержат хлорофилл», «все грибы — растения», из которой нельзя получить никакого вывода о грибах, так как средний термин («растения») не распределен ни в одной из посылок, и отношение между S и Р остается слишком неопределенным для вывода.

Вместо этого мы, допустив ложную посылку «все растения содержат хлорофилл», получили также ложный вывод: — «все грибы содержат хлорофилл».

Из сказанного видно, что первое необходимое условие правильного силлогизма составляет истинность посылок, на которых основывается вывод по существу их содержания. Если посылки ложны, то они не могут быть достаточным основанием для правильного по содержанию вывода.

Таким образом, даже самое точное соблюдение логических правил силлогизма еще не обеспечивает само по себе истинности заключения. Соблюдение правил силлогизма дает истинное заключение только при условии истинности посылок, т. е. соответствия посылок действительным фактам.

Всякий силлогизм предполагает (пусть иногда ошибочно) истинность посылок; помня об этом, мы вправе мысленно отвлекаться от вопроса об истинности посылок и сосредоточиваться только на вопросе о логической связи между посылками и выводом, т. е. на вопросе о том, вытекает ли данный вывод из данных (и всегда предполагаемых истинными) посылок или нет.

Рассматриваемые с этой точки зрения выводы могут быть правильными или неправильными. Правильными они будут, если посылки удовлетворяют всем общим и специальным условиям фигур, необходимым для получения из них вывода. Неправильными они будут, если вывод сделан вопреки этим условиям.

Логические ошибки, встречающиеся в силлогизмах

Некоторые из логических ошибок неправильного вывода, особенно часто встречающиеся в практике мышления, заслуживают быть особо отмеченными.

Одна из наиболее частых здесь ошибок состоит в том, что, умозаключая по первой фигуре, делают вывод при отрицательной меньшей посылке.

Все студенты обязаны держать экзамены.

Аспиранты — не студенты.

——————————————————

Аспиранты не обязаны держать экзамены.

Вывод явно ошибочный. Но если он логически невозможен, то почему же подобная ошибка возможна фактически? Одним из ее источников является неправильное истолкование смысла большей посылки. Если, услышав, что «все студенты обязаны держать экзамены», мы истолкуем это положение в том смысле, будто «одни лишь студенты обязаны держать экзамены», то наш вывод примет следующий вид:

Только студенты обязаны держать экзамены.

Аспиранты — не студенты.

————————————————————

Аспиранты не обязаны держать экзамены.

Признав эти посылки истинными, мы сделали из них правильный вывод, т. е. вывод здесь необходимо следует из принятых посылок. Ошибка здесь не в том, что мы игнорировали известное правило о распределенности большего термина, распределенного в выводе, а в том, что, неправильно истолковав смысл большей посылки, мы получили посылку, ложную по существу, а потому получили и ложный вывод.

Вторая встречающаяся в практике силлогистических выводов ошибка состоит в том, что делают вывод по второй фигуре из двух утвердительных посылок.

Пример:

Все рыбы имеют плавники.

Это животное имеет плавники.

——————————————

Это животное — рыба.

Здесь вывод — явно ошибочный. Так как средний термин в обеих посылках является предикатом утвердительного суждения, выражающего подчинение понятий, то он не распределен ни в одной из посылок. Поэтому никакой вывод здесь невозможен. И «рыбы», и «это животное» входят в объем понятия «животные, имеющие плавники». Но так как из посылок неизвестно, в какую именно часть этого объема входят «рыбы», в какую — «это животное», то отношение «этого животного» к «рыбам» остается совершенно невыясненным; возможно, что «это животное» и есть «рыба», и возможно, что оно не есть «рыба».

Однако и в подобном случае ошибка обычно состоит не столько в нарушении известного правила о распределенности среднего термина, сколько в неправильном истолковании смысла большей посылки. Кто услышал суждение «все рыбы имеют плавники» в смысле «только рыбы имеют плавники», тот, очевидно, сделает следующий вывод.

Все животные, имеющие плавники, — рыбы.

Это животное имеет плавники.

————————————————————

Это животное есть рыба.

В этом выводе заключение было бы необходимо истинным, если бы были истинными обе посылки. Но большая посылка ложна, и потому вывод также ложен.

Третья ошибка, часто встречающаяся в практике выводов, называется «учетверением терминов». Она состоит в том, что делают вывод из двух посылок, в которые входят не три, а четыре термина.

Пример такой ошибки:

Всякое сгорание дает в остатке золу и пепел.

Всякое окисление есть сгорание.

————————————————————

Всякое окисление дает в остатке золу и пепел.

Так как связь понятий, входящих в вывод, не видна сразу, то она может быть установлена только через третье понятие, отношение которого к большему и меньшему терминам было бы известно из посылок. Но в нашем примере эта связь не может быть установлена: здесь в посылках устанавливается не отношение большего или меньшего понятия к третьему понятию, а устанавливается в одной посылке отношение большего термина к третьему понятию («сгорание» в химическом смысле, т. е. процесс, который не обязательно сопровождается появлением золы и пепла), а в другой — отношение меньшего термина к четвертому понятию («сгорание» в повседневном ненаучном смысле, означающее процесс, при котором в остатке всегда получаются зола и пепел). Не удивительно, что, не будучи связаны между собой через третье понятие в посылках, больший и меньший термины не могут оказаться связанными в выводе.

И здесь основа ошибки не столько в нарушении правила о количестве терминов, входящих в силлогизм, сколько в двусмысленности слова «сгорание», которое имеет не одно значение, а два, выражает два понятия.

К дедуктивным можно отнести и умозаключения с отношением.

Умозаключение, посылки и вывод которого являются суждениями с отношениями, называется умозаключением с отношениями.

Например:

Андрей — брат Павла.

Павел — брат Сергея.

———————————

Андрей — брат Сергея.

Легко убедиться, что это особый вид дедуктивного умозаключения, он не может рассматриваться как простой категорический силлогизм, посылками и заключением которого являются категорические суждения, имеющие субъектно-предикатную структуру. Заключение здесь получено из суждений с отношениями, логическая структура которых выражается формулой а R в.

Логическим основанием умозаключений из суждений с отношениями являются свойства отношений, важнейшие из которых — симметричность, рефлексивность и транзитивность.

Отношение симметричности. Отношение называется симметричным, если для любых предметов х и у данного класса верно, что если предмет х находится в каком-то отношении к предмету у, то и предмет у находится в этом отношении к предмету х. Таково отношение соседства («если Иван — сосед Петра, то и Петр — сосед Ивана»), отношение подобия геометрических фигур («если треугольник АВС подобен треугольнику А1В1С1, то и треугольник А1В1С1 подобен треугольнику АВС»).

Отношение симметричности символически записывается так:

a R a 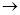b R a.

Отношение рефлексивности. Некоторое отношение, имеющее место среди предметов определенного класса, называется рефлексивным, если каждый предмет этого класса находится в данном отношении к самому себе. Например: рефлексивным является отношение равенства каждого числа самому себе (х = х). Также рефлексивным является отношение тождества мыслей самим себе в процессе правильного рассуждения (А тождественно А).

Отношение рефлексивности символически записывается так:

a R b 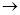a R a 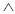b R b.

Отношение транзитивности. Отношение называется транзитивным, если из наличия этого отношения между предметами х и у, а также между у и z, следует его наличие между х и z. Например: «Москва больше Саратова, Саратов больше Пензы, следовательно, Москва больше Пензы». Этот пример иллюстрирует транзитивность отношения «больше». Однако отношения «любить», «ненавидеть», «зависеть», «владеть» не обладают свойством транзитивности. Поэтому нетранзитивность отношения «любить» в суждениях «Каренин любил Анну», «Анна любила Вронского» не позволяет нам сделать заключение «Каренин любил Вронского».

Отношение транзитивности символически записывается так:

(a R b 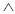b R c) 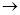a R c.

Дедуктивные умозаключения из сложных суждений

Дедуктивные умозаключения могут строиться не только из простых, но и из сложных суждений. В зависимости от видов сложных суждений различают и виды дедукции.

Чисто условное умозаключение — это умозаключение, обе посылки и заключение которого являются условными суждениями. Например:

Если средства производства находятся в руках всего общества (а), то члены общества находятся в равном отношении к средствам производства (в).

Если члены общества находятся в равном отношении к средствам производства (в), то между ними устанавливаются отношения сотрудничества и взаимопомощи (с).

Если средства производства находятся в руках всего общества (а), то между членами общества устанавливаются отношения сотрудничества и взаимопомощи (с).

В приведенном примере обе посылки — условные суждения, причем основанием второй посылки является следствие первой (в), из которого в свою очередь вытекает некоторое следствие (с). Общая часть двух посылок (в) позволяет связать основание первой (а) и следствие второй (с). Поэтому заключение также выражается в форме условного суждения.

Схема чисто условного умозаключения

Если а, то в,

если в, то с

––––––––––

Если а, то с

Вывод в чисто условном умозаключении основывается на правиле: «Следствие следствия есть следствие основания».

Условно-категорическое умозаключение — умозаключение, одна из посылок которого является условным суждением, другая — простым категорическим суждением.

Условно-категорическое умозаключение имеет только два правильных модуса: модус утверждающий и модус отрицающий.

1. Модус утверждающий.

Если по проводнику идет ток, то проводник нагревается.

По проводнику идет ток.

––––––––––––––––––––––––––––––––––––––––––––––––––

Следовательно, проводник нагревается.

2. Модус отрицающий.

Если по проводнику идет ток, то проводник нагревается.

Проводник не нагревается.

–––––––––––––––––––––––––––––––––––––––––––––––

Следовательно, по нему ток не идет.

Следует отметить, что два других модуса достоверных заключений не дают. Они называются неправильными модусами и подчиняются правилу: «Отрицание основания не ведет с необходимостью к отрицанию следствия и утверждение следствия не ведет с необходимостью к утверждению основания».

3. Если по проводнику идет ток (а), то проводник нагревается (в).

По проводнику не идет ток (не-а).

–––––––––––––––––––––––––––––––––––––––––––––––––––––

Следовательно, проводник не нагревается (не-в).

4. Если по проводнику идет ток (а), то проводник нагревается (в).

Проводник нагревается (в).

–––––––––––––––––––––––––––––––––––––––––––––––––––––

Следовательно, по проводнику идет ток (а).

В нашей условной посылке в первом случае при наличии основания («Если по проводнику идет ток») утверждается наличие следствия («то проводник нагревается»), в категорической посылке подтверждается наличие основания, поэтому в заключении мы уверенно утверждаем наличие следствия.

Во втором случае условная посылка условно-категорического умозаключения, как правило, обладает следующим примечательным свойством. Ее основание является достаточным, но не необходимым для наличия следствия. Если мы зафиксировали, что по проводнику идет ток, то этого достаточно, чтобы безошибочно утверждать: «Проводник нагревается». Но это условие не является необходимым, так как при отсутствии тока проводник может нагреваться, например, от солнечных лучей. С другой стороны, следствие условной посылки является необходимым для наличия основания, так как без факта нагревания проводника не может быть и факта прохождения через проводник тока. Но следствия не достаточно для наличия основания, поскольку проводник может подогреваться ближайшей отопительной батареей, а тока в нем не будет.

Разделительно-категорическое умозаключение — это такое, в котором одна из посылок — суждение разделительное, а другая — суждение категорическое.

Треугольники бывают либо тупоугольными, либо остроугольными, либо прямоугольными.

Данный треугольник тупоугольный.

——————————————————————————————————————

Следовательно, данный треугольник не является ни прямоугольным, ни остроугольным.

Разделительно-категорическое умозаключение имеет два модуса, или вида. Один модус называется «модус утверждающе-отрицающий». Пример выше. Здесь от утверждения одного из случаев, указанных в разделительной посылке, мы идем к отрицанию остальных. Второй модус носит название «модус отрицающе-утверждающий». Пример:

Войны бывают справедливые или захватнические.

Эта война не является справедливой.

——————————————————————

Следовательно, эта война — захватническая.

Здесь от отрицания одного (возможно, нескольких) случая мы идем к утверждению оставшихся.

Разделительно-категорическое умозаключение должно подчиняться двум основным правилам. Во-первых, в разделительной посылке все перечисленные в ней случаи должны строго исключать друг друга. Следующее рассуждение ошибочно.

Л. Н. Толстой — романист или драматург.

Л. Н. Толстой — романист.

———————————————————

Следовательно, Л. Н. Толстой не драматург.

В этом примере указанные случаи разделительной посылки строго не исключают друг друга, так как писатель может быть одновременно и романистом, и драматургом. Поэтому заключение здесь получилось ложным.

Во-вторых, в разделительной посылке должны быть перечислены все возможные случаи. Если это условие не соблюдено, мы не можем быть уверены в истинности полученного заключения.

Условно-разделительное (лемматическое) умозаключение — в нем одна посылка — разделительное суждение, остальные — условные суждения.

Разделительное суждение может содержать две, три и большее число альтернатив, поэтому лемматические умозаключения делятся на дилеммы (две альтернативы), трилеммы (три альтернативы) и т. д.

Различают два вида дилемм: конструктивную (созидательную) и деструктивную (разрушительную), — каждая из которых делится на простую и сложную дилемму.

В простой конструктивной дилемме условная посылка содержит два основания, из которых вытекает одно и то же следствие. Разделительная посылка утверждает оба возможных основания, заключение утверждает следствие. Рассуждение направлено от утверждения истинности оснований к утверждению истинности следствия.

Схема простой конструктивной дилеммы:

Если а, то с; если в то с

а или в

–––––––––––––––––––

с

Например:

Если обвиняемый виновен в воровстве (а), то он подлежит уголовной ответственности (с); если он виновен в грабеже (в), то он также подлежит уголовной ответственности (с).

Обвиняемый виновен или в воровстве (а), или в грабеже (в).

––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––

Обвиняемый подлежит уголовной ответственности (с).

В сложной конструктивной дилемме условная посылка содержит два основания и два следствия. Разделительная посылка утверждает оба возможных основания, заключение утверждает оба возможных следствия. Рассуждение направлено от утверждения истинности оснований к утверждению истинности следствий.

Схема сложной конструктивной дилеммы:

Если а, то в; если с, то d

а или с

–––––––––––––––––––––

в или d

Например:

Если философ признает первичной материю (а), значит, он принадлежит к лагерю материалистов (в); если он считает первичным сознание (с), то он принадлежит к идеалистическому лагерю (d).

Но философ может признавать первичным или материю (а), или сознание (с).

––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––

Философ принадлежит либо к лагерю материалистов (в), либо к лагерю идеалистов (d).

В простой деструктивной дилемме условная посылка содержит одно основание, из которого вытекают два возможных следствия. Разделительная посылка отрицает оба следствия, заключение отрицает основание. Рассуждение направлено от отрицания истинности следствий, к отрицанию истинности основания.

Схема простой деструктивной дилеммы:

Если а, то в; если а, то с

Не-в или не-с

–––––––––––––––––––––

Не-а

Если Н. — подозреваемый (а), значит, он или задержан по подозрению в совершении преступления (в), или является лицом, к которому применена мера пресечения до предъявления обвинения (с).

Н. не был задержан по