
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
IІ курс, ІII семестр
|
|
КЗ3: №№ 521, 531, 541, 551, 571.
Всі номери прикладів взяті з методичного посібника для студентів-заочників “Высшая математика” под ред. Артюнова Ю.С. М.: Высшая школа, 1985г.
Нижче наведені приклади для самостійного розв’язання при підготовці до іспиту. Обов’язковим є виконання студентом завдань свого варіанту.
1-10. Дано вектори 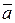 (a 1, a 2, a 3),
(a 1, a 2, a 3), 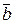 (b 1, b 2, b 3),
(b 1, b 2, b 3), 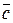 (c 1, c 2, c 3) і
(c 1, c 2, c 3) і 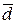 (d 1, d 2, d 3) у деякому базисі. Показати, що вектори
(d 1, d 2, d 3) у деякому базисі. Показати, що вектори 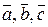 утворюють базис і знайти координати вектора
утворюють базис і знайти координати вектора 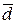 у цьому базисі.
у цьому базисі.
1. 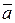 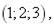
| 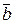 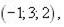
| 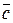 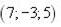
| 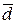 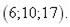
|
2. 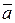 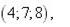
| 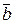 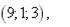
| 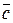 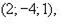
| 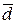 
|
3. 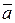 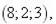
| 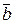 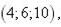
| 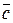 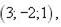
| 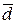 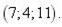
|
4. 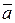 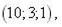
| 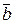 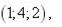
| 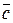 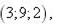
| 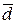 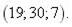
|
5. 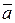 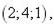
| 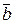 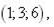
| 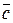 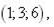
| 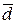 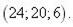
|
6. 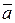 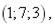
| 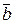 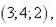
| 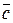 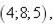
| 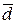 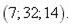
|
7. 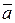 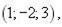
| 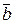 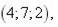
| 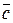 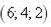
| 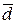 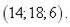
|
8. 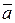 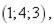
| 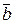 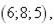
| 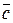 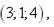
| 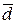 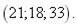
|
9. 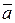 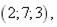
| 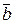 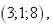
| 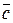 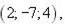
| 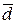 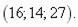
|
10. 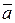 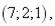
| 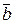 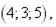
| 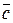 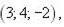
| 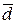 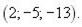
|
11-20. Дано координати вершин піраміди 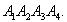 Знайти:
Знайти:
1) довжину ребра 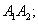
2) кут між ребрами 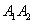 і
і 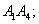
3) кут між ребром 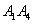 і гранню
і гранню 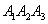 ;
;
4) площу грані 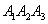
5) об’єм піраміди;
6) рівняння прямої 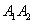 ;
;
7) рівняння площини 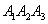 ;
;
8) рівняння висоти, опущеної з вершини 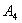 на грань
на грань 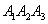 . Зобразити на рисунку.
. Зобразити на рисунку.
| 11. А 1(4; 2; 5), | А 2(0; 7; 2), | А 3(0; 2; 7), | А 4(1; 5; 0). |
| 12. А 1(4; 4; 10), | А 2(4; 10; 2), | А 3(3; 8; 4), | А 4(9; 6; 4). |
| 13. А 1(4; 6; 5), | А 2(6; 9; 4), | А 3(2; 10; 10), | А 4(7; 5; 9). |
| 14. А 1(3; 5; 4), | А 2(8; 7; 4), | А 3(5; 10; 4), | А 4(4; 7; 8). |
| 15. А 1(10; 6; 6), | А 2(-2; 8; 2), | А 3(6; 8; 9), | А 4(4; 10; 3). |
| 16. А 1(1; 8; 2), | А 2(5; 2; 6), | А 3(5; 7; 4), | А 4(4; 10; 9). |
| 17. А 1(6; 6; 5), | А 2(4; 9; 5), | А 3(4; 6; 11), | А 4(6; 9; 3). |
| 18. А 1(7; 2; 2), | А 2(5; 7; 7), | А 3(5; 3; 1), | А 4(2; 3; 7). |
| 19. А 1(8; 6; 4), | А 2(10; 5; 5), | А 3(5; 6; 8), | А 4(8; 10; 7). |
| 20. А 1(7; 7; 3;), | А 2(6; 5; 8), | А 3(3; 5; 8), | А 4(8; 4; 1). |
51-60. Дано систему лінійних рівнянь
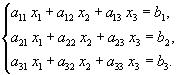
Довести її сумісність і розв’язати двома способами: 1) методом Гауса; 2) засобами матричного числення.
51. 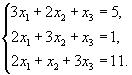 52.
52. 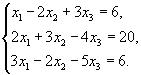
53.  54.
54. 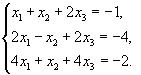
55. 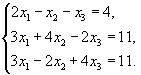 56.
56. 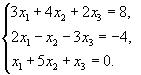
57. 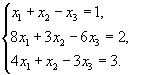 58.
58. 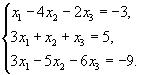
59. 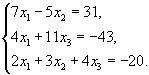 60.
60. 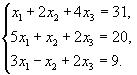
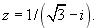
111-120. Знайти границі функцій, не користуючись правилом Лопіталя.
111. а) 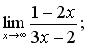 б)
б) 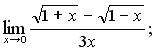
в) 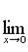
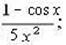 г)
г) 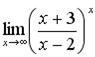 .
.
112. а) 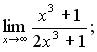 б)
б) 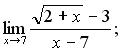
в) 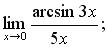 г)
г) 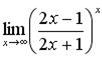 .
.
113. а) 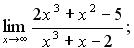 б)
б) 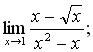
в) 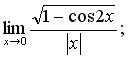 г)
г) 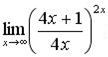 .
.
114. а) 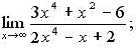 б)
б) 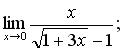
в)  г)
г) 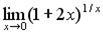 .
.
115. а) 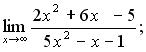 б)
б) 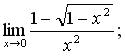
в) 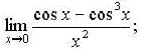 г)
г) 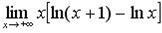 .
.
116. а) 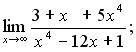 б)
б) 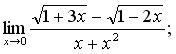
в) 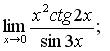 г)
г) 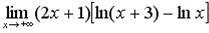 .
.
117. а) 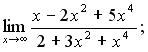 б)
б) 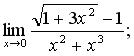
в) 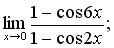 г)
г) 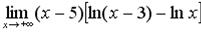 .
.
118. а) 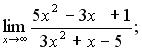 б)
б) 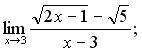
в) 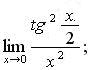 г)
г) 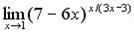 .
.
119. а) 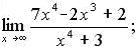 б)
б) 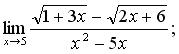
в) 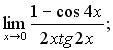 г)
г) 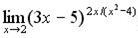 .
.
120. а) 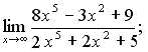 б)
б) 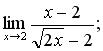
в) 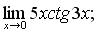 г)
г) 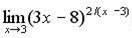 .
.
131-140. Задано функцію y = f (x). Знайти точки розриву функції, якщо вони існують. Побудувати графік.
131. 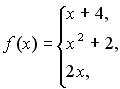
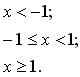
132. 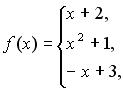
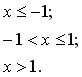
133. 
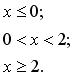
134. 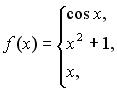
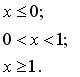
135. 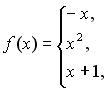
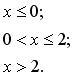
136. 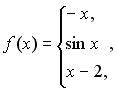

137. 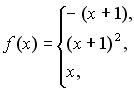
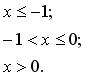
138. 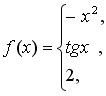
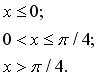
139. 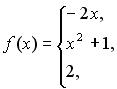
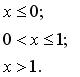
140. 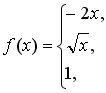

141-150. Знайти похідні 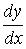 даних функцій.
даних функцій.
141. а) 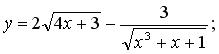
б) 
в) 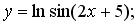
г) 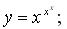
д) 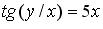 .
.
142. а) 
б) 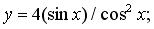
в) 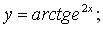
г) 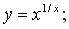
д) 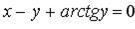 .
.
143. а) 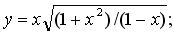
б) 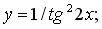
в) 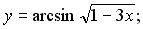
г) 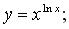
д) 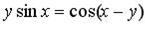 .
.
144. а) 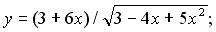
б) 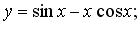
в) 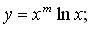
г) 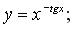
д) 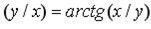 .
.
145. а) 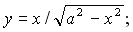
б) 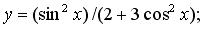
в) 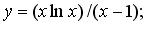
г) 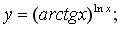
д) 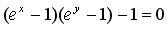 .
.
146. а) 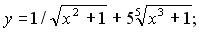
б) 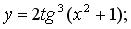
в) 
г) 
д) 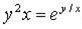 .
.
147. а) 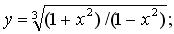
б) 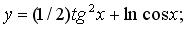
в) 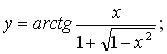
г) 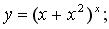
д)  .
.
148. а) 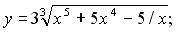
б) 
в) 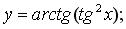
г) 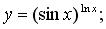
д) 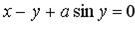 .
.
149. а) 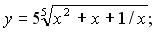
б) 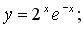
в) 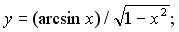
г) 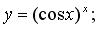
д) 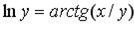 .
.
150. а) 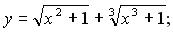
б) 
в) 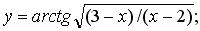
г) 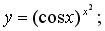
д) 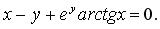
191-210. Дослідити методами диференціального числення функцію y = f (x) і, використовуючи результати дослідження, побудувати її графік.
191. 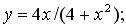 192.
192. 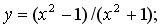
193.  194.
194. 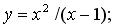
195. 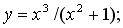 196.
196. 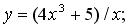
197. 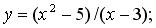 198.
198. 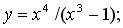
199. 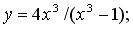 200.
200. 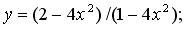
201. 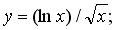 202.
202. 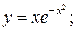
203. 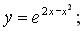 204.
204. 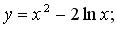
205. 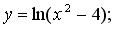 206.
206. 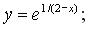
207. 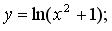 208.
208. 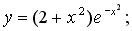
209.  210.
210. 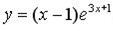 .
.
251-260. Знайти найменше і найбільше значення функції z = f (x; y) у замкнутій області D, заданою системою нерівностей. Побудувати графік.
251.  ;
; 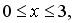
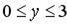 .
.
252. 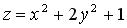 ;
; 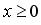 ,
, 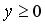 ,
, 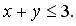
253. 
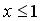 ,
, 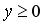 ,
,  .
.
254. 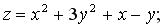
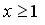 ,
, 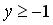 ,
, 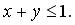
255. 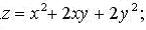
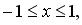
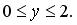
256. 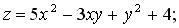
 ,
, 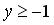 ,
, 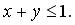
257. 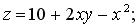
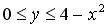 .
.
258. 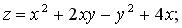
 ,
, 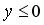 ,
, 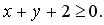
259. 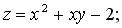
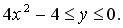
260. 
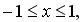
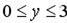 .
.
281-290. Знайти невизначені інтеграли. У п. а) і б) результати перевірити диференціюванням.
281. a) 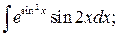 б)
б) 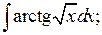
в) 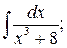 г)
г) 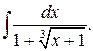
282. a) 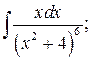 б)
б) 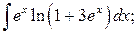
в) 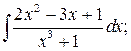 г)
г) 
283. a) 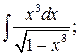 б)
б) 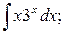
в) 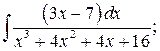 г)
г) 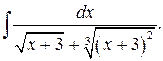
284. a)  б)
б) 
в) 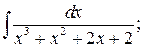 г)
г) 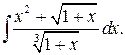
285. a) 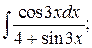 б)
б) 
в) 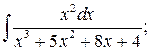 г)
г) 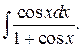
286. a)  б)
б) 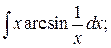
в) 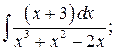 г)
г) 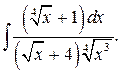
287. a) 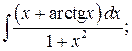 б)
б) 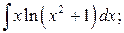
в) 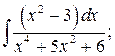 г)
г) 
288. а)  б)
б) 
в)  г)
г) 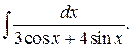
289. а) 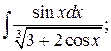 б)
б) 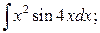
в)  г)
г) 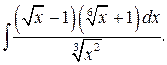
290. а) 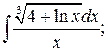 б)
б) 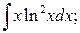
в) 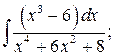 г)
г) 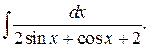
301-310. Обчислити невласний інтеграл або довести його розбіжність.
301. 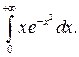 302.
302. 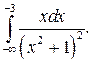
303. 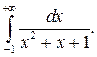 304.
304. 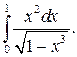
305. 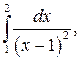 306.
306. 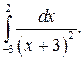
307. 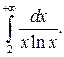 308.
308. 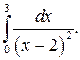
309. 
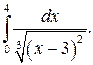 310.
310. 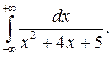
321-340. Знайти загальний розв’язок диференціального рівняння.
321. 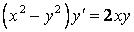 .
.
322. 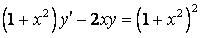 .
.
323. 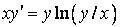 .
.
324. 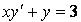 .
.
325. 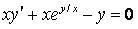 .
.
326. 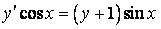 .
.
327. 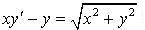 .
.
328. 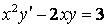 .
.
329. 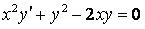 .
.
330. 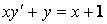 .
.
331. 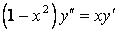 .
.
332. 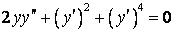 .
.
333. 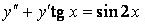 .
.
334. 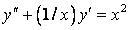 .
.
335. 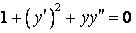 .
.
336. 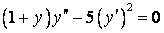 .
.
337. 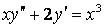 .
.
338. 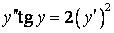 .
.
339. 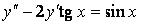 .
.
340. 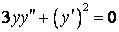 .
.
341-350. Знайти частковий розв’язок диференціального рівняння 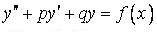 , що задовольняє початковим умовам
, що задовольняє початковим умовам 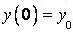 ,
, 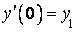 .
.
341. 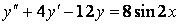 ;
; 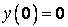 ,
, 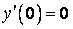 .
.
342. 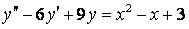 ;
; 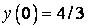 ,
, 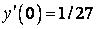 .
.
343. 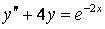 ;
;  ,
, 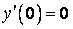 .
.
344.  ;
; 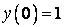 ,
, 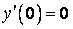 .
.
345. 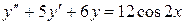 ;
; 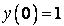 ,
, 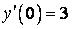 .
.
346. 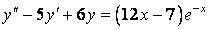 ;
;  ,
, 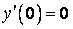 .
.
347. 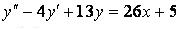 ;
; 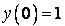 ,
, 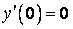 .
.
348. 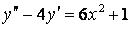 ;
; 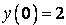 ,
, 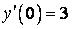 .
.
349. 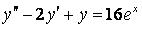 ;
; 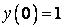 ,
, 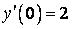 .
.
350. 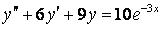 ;
; 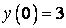 ,
, 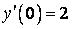 .
.
421-430. Дослідити збіжність числового ряду 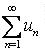 .
.
421. 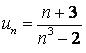 .
.
422. 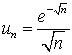 .
.
423. 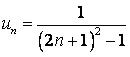
424. 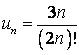 .
.
425. 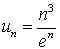 .
.
426. 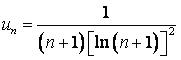 .
.
427.  .
.
428. 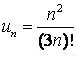 .
.
429. 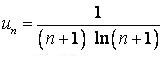 .
.
430. 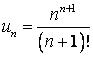 .
.
431-440. Знайти інтервал збіжності степеневого ряда 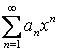 .
.
431. 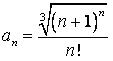 .
.
432. 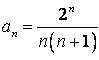 .
.
433. 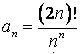 .
.
434. 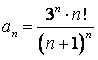 .
.
435. 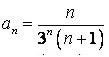 .
.
436. 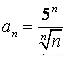 .
.
437. 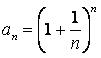 .
.
438. 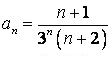 .
.
439. 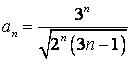 .
.
440. 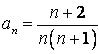 .
.
441-450. Обчислити визначений інтеграл 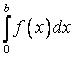 з точністю до 0, 001, розклавши підінтегральну функцію у степеневий ряд і потім проінтегрувавши його почленно.
з точністю до 0, 001, розклавши підінтегральну функцію у степеневий ряд і потім проінтегрувавши його почленно.
441. 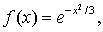
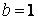 .
.
442. 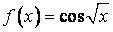 ,
, 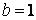 .
.
443. 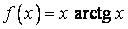 ,
, 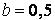 .
.
444. 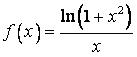 ,
,  .
.
445. 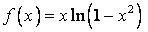 ,
,  .
.
446.  ,
,  .
.
447. 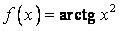 ,
,  .
.
448. 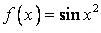 ,
, 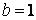 .
.
449. 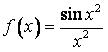 ,
,  .
.
450. 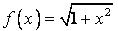 ,
,  .
.
521. Студент знає 45 з 60 питань програми. Кожний екзаменаційний білет містить три питання. Знайти ймовірність того, що студент знає: а) всі три питання; б) тільки два питання; в) тільки одне питання екзаменаційного білета.
522. В кожній з двох урн знаходяться 5 білих і 10 чорних куль. З першої урни переложили до другої навмання одну кулю, а потім з другої урни витягли навмання одну кулю. Знайти ймовірність того, що вийнята куля виявиться чорною.
523. Три стрільці в однакових і незалежних умовах зробили по одному пострілу по одній і тій самій цілі. Ймовірність влучення у ціль першим стрільцем дорівнює 0, 9, другим – 0, 8, третім – 0, 7. Знайти ймовірність того, що: а) тільки один із стрільців влучив у ціль; б) тільки два стрільця влучили у ціль; в) всі три стрільця влучили у ціль.
524. Ймовірність, що подія відбудеться в кожному з однакових і незалежних випробуваннях дорівнює 0, 8. Знайти ймовірність того, що в 1600 випробуваннях подія відбудеться 1200 раз.
525. Для сигналізації про аварію установлені три незалежно працюючих прилади. Ймовірність того, що при аварії запрацює перший прилад, дорівнює 0, 9, другий – 0, 95, третій – 0, 85. Знайти ймовірність того, що при аварії запрацює: а) тільки один прилад; б) тільки два прилади; в) всі три прилади.
526. Ймовірність, що подія відбудеться в кожному з однакових і незалежних випробуваннях дорівнює 0, 02. Знайти ймовірність того, що в 150 випробуваннях подія відбудеться 5 раз.
527. У партії з 1000 виробів знаходяться 10 дефектних. Знайти ймовірність того, що поміж 50 виробів, узятих навмання з цієї партії, рівно три виявляться дефектними.
528. Ймовірність, що подія відбудеться в кожному з однакових і незалежних випробуваннях дорівнює 0, 8. Знайти імовірність того, що в 125 випробуваннях подія відбудеться не менше, ніж 75, і не більше, ніж 90 разів.
529. На трьох верстатах при однакових і незалежних умовах виробляються деталі одного найменування. На першому верстаті виробляють 10%, на другому – 30%, на третьому – 60% всіх деталей. Ймовірність кожної деталі бути стандартною дорівнює 0, 7, якщо вона вироблена на першому верстаті, 0, 8 – якщо на другому верстаті, і 0, 9 – якщо на третьому верстаті. Знайти ймовірність того, що навмання взята деталь виявиться стандартною.
530. Два брати входять до складу двох спортивних команд, що складаються з 12 осіб кожна. У двох урнах містяться по 12 білетів з номерами від 1 до 12. Члени кожної команди виймають навмання по одному білету з окремої урни (без повернення). Знайти ймовірність того, що обидва брати витягнуть білет номер 6.
531-540. Дискретна випадкова величина х може приймати тільки два значення: 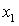 и
и 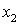 , до того ж
, до того ж 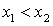 . Відомі ймовірність
. Відомі ймовірність 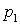 можливого значення
можливого значення  , математичне очікування
, математичне очікування 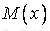 і дисперсія
і дисперсія 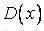 . Знайти закон розподілу цієї випадкової величини.
. Знайти закон розподілу цієї випадкової величини.
531. 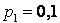 ;
; 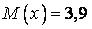 ;
; 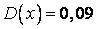 .
.
532. 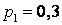 ;
; 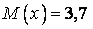 ;
; 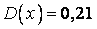 .
.
533. 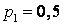 ;
; 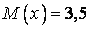 ;
; 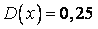 .
.
534. 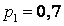 ;
; 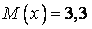 ;
; 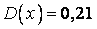 .
.
535. 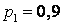 ;
; 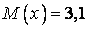 ;
; 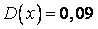 .
.
536. 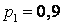 ;
; 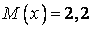 ;
; 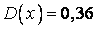 .
.
537. 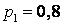 ;
; 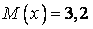 ;
; 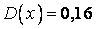 .
.
538. 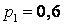 ;
; 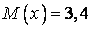 ;
; 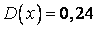 .
.
539. 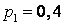 ;
; 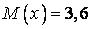 ;
; 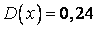 .
.
540.  ;
; 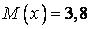 ;
; 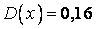 .
.
541-550. Випадкова величина х задана функцією розподілу 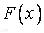 . Знайти щільність розподілу ймовірностей, математичне очікування і дисперсію випадкової величини.
. Знайти щільність розподілу ймовірностей, математичне очікування і дисперсію випадкової величини.
541. 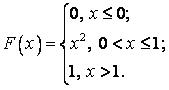
542. 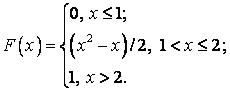
543. 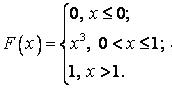
544. 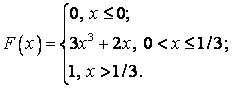
545. 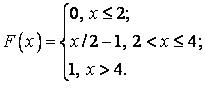
546. 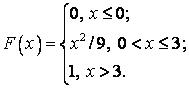
547. 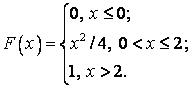
548. 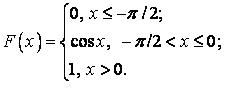
549. 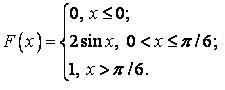
550. 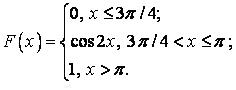
551-560. Відомі математичне очікування 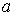 і середнє квадратичне відхилення
і середнє квадратичне відхилення 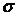 нормально розподіленої випадкової величини х. Знайти ймовірність попадання цієї величини в заданий інтервал
нормально розподіленої випадкової величини х. Знайти ймовірність попадання цієї величини в заданий інтервал 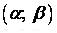 .
.
551. 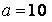 ,
, 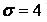 ,
, 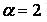 ,
, 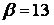 .
.
552. 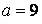 ,
, 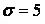 ,
, 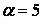 ,
, 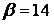 .
.
553. 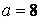 ,
,  ,
, 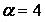 ,
, 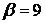 .
.
554. 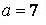 ,
, 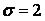 ,
, 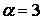 ,
, 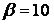 .
.
555. 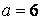 ,
, 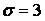 ,
, 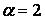 ,
, 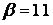 .
.
556. 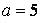 ,
, 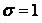 ,
, 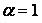 ,
,  .
.
557. 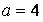 ,
, 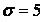 ,
, 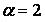 ,
, 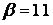 .
.
558. 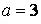 ,
,  ,
, 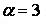 ,
, 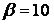 .
.
559. 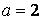 ,
, 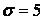 ,
, 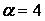 ,
, 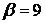 .
.
560. 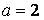 ,
, 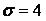 ,
, 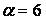 ,
, 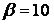 .
.
571-580. Знайти довірчий інтервал для оцінки математичного очікування 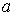 нормального розподілу з надійністю 0, 95, знаючи вибіркову середню
нормального розподілу з надійністю 0, 95, знаючи вибіркову середню 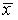 , об’єм виборки
, об’єм виборки 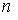 і середнє квадратичне відхилення
і середнє квадратичне відхилення 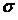 .
.
571. 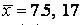 ,
, 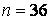 ,
, 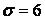 .
.
572. 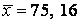 ,
, 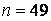 ,
, 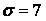 .
.
573. 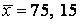 ,
, 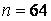 ,
, 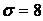 .
.
574. 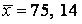 ,
, 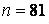 ,
, 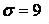 .
.
575. 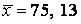 ,
, 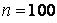 ,
,  .
.
576. 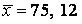 ,
, 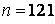 ,
, 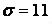 .
.
577. 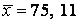 ,
, 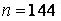 ,
, 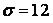 .
.
578.  ,
, 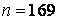 ,
, 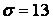 .
.
579. 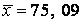 ,
, 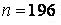 ,
, 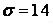 .
.
580.  ,
, 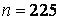 ,
, 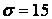 .
.