
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение перемещений сечения K балки
|
|
Для определения перемещений (прогиб и угол поворота) сечения K балки вычислим интеграл Мора, используя формулу Симпсона и формулу Верещагина (графо-аналитический способ). При этом необходимо:
1) Построить вспомогательную расчетную схему и нагрузить ее единичной нагрузкой в точке, где требуется определить перемещение. При определении линейных перемещений в заданном направлении прикладывается единичная сила, при определении угловых перемещений – единичный момент.
2) Определить значения ординат в контролируемых сечениях для вспомогательной расчетной схемы и построить соответствующую эпюру изгибающих моментов.
3) Вычислить по всем участкам расчетной схемы интегралы Мора по формуле Симпсона или формуле Верещагина, используя эпюры изгибающих моментов от заданной и единичной нагрузок.
4) Если вычисленное перемещение имеет положительный знак, то это значит, что его направление совпадает с направлением единичной нагрузки. Отрицательный знак указывает на то, что действительное перемещение противоположно направлению единичной силы.
5.1. Назначение вспомогательных расчетных схем.
Вспомогательная расчетная схема (ВРС) получается из ЗРС путем замены заданной внешней нагрузки на вспомогательную (для перемещения каждого вида – отдельная нагрузка единичного значения), см. рис. 19.
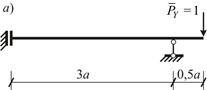
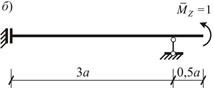
Рис. 19
Для каждой из ВРС требуется построить эпюру изгибающих моментов, которая именуется «направляющей» («единичной»). Причем способ построения применяется тот же, что и при построении эпюры от заданной нагрузки: используются те же уравнения равновесия как для определения опорных реакций, так и для определения значений ординат изгибающего момента в контролируемых сечениях.
5.2. Построение направляющей эпюры изгибающих моментов от действия вертикальной единичной сосредоточенной силы 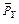 в сечении K.
в сечении K.
5.2.1. Определение опорных реакций.
Заменим опорные связи (рис. 19 а) на опорные реакции (рис. 20), причем одной реакции соответствует один опорный стержень. Реакции до их определения считаются положительно направленными.
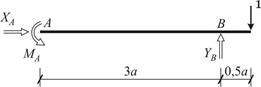
Рис. 20
Найдем неизвестные реакции, используя уравнения равновесия, описанные в п. 2 при определении опорных реакций от заданной нагрузки:
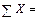
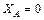 ;
;
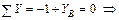
 ;
;
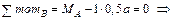
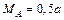 .
.
Заменяя введенные на рис. 20 обозначения реакций найденными векторами, получаем рис. 21 и используем его для проведения контроля правильности определения реакций опорных связей.
Контроль: 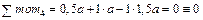 .
.
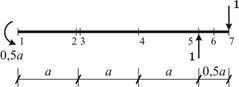
Рис. 21
Количество контролируемых сечений принимается равным числу сечений, назначенных в п. 3.1 для ЗРС (см. рис. 21). Однако для построения направляющейэпюры изгибающих моментов 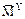 достаточно определить ординаты в сечениях 1, 5 и 7 (см. п. 3.1), при этом будем иметь два участка с линейным законом изменения изгибающего момента (1–5 и 5–7), см. Приложение 1.
достаточно определить ординаты в сечениях 1, 5 и 7 (см. п. 3.1), при этом будем иметь два участка с линейным законом изменения изгибающего момента (1–5 и 5–7), см. Приложение 1.
5.2.2. Определение значений ординат и построение направляющейэпюры изгибающих моментов 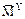 .
.
Найдем значения момента в контролируемых сечениях 1, 5 и 7 (рис. 22).
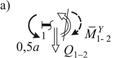
| 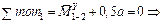
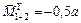 (РВ/В). (РВ/В).
|
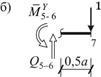
| 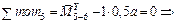
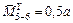 (РВ/В). (РВ/В).
|
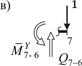 Рис. 22
Рис. 22
| 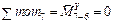 . .
|
Полученные данные используем для построения направляющейэпюры изгибающих моментов 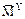 на растянутых волокнах (рис. 23).
на растянутых волокнах (рис. 23).

Рис. 23
Значения ординат в оставшихся сечениях 2, 3, 4 и 6 необходимые для дальнейшего расчета легко можно получить, используя эпюру (рис. 23).
5.3. Определение прогиба сечения K балки.
Для определения перемещений сечения K балки воспользуемся формулой Симпсона и формулой Верещагина (графо-аналитический способ).
В случае если эпюра M от заданной нагрузки очерчена по квадратной параболе или прямой, а эпюра 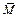 от единичной нагрузки имеет прямолинейное очертание эффективно применение формулы Симпсона:
от единичной нагрузки имеет прямолинейное очертание эффективно применение формулы Симпсона:
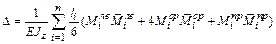 , (4)
, (4)
где 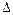 – перемещение сечения балки (прогиб
– перемещение сечения балки (прогиб 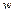 или угол поворота
или угол поворота 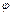 );
);
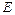 – модуль упругости материала балки;
– модуль упругости материала балки;
 – момент инерции площади сечения балки относительно нейтральной оси Z;
– момент инерции площади сечения балки относительно нейтральной оси Z;
 – длина участка i балки;
– длина участка i балки;
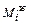 ,
, 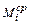 ,
, 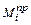 – соответственно крайние левые, средние и крайние правые ординаты участка i эпюры изгибающих моментов M от заданной нагрузки;
– соответственно крайние левые, средние и крайние правые ординаты участка i эпюры изгибающих моментов M от заданной нагрузки;
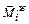 ,
, 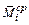 ,
, 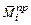 – соответственно крайние левые, средние и крайние правые ординаты участка i эпюры изгибающих моментов
– соответственно крайние левые, средние и крайние правые ординаты участка i эпюры изгибающих моментов 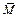 от единичной нагрузки.
от единичной нагрузки.
В случае если эпюра M от заданной нагрузки и эпюра 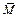 от единичной нагрузки имеют прямолинейное очертание эффективно применение графо-аналитического способа(формулы Верещагина):
от единичной нагрузки имеют прямолинейное очертание эффективно применение графо-аналитического способа(формулы Верещагина):
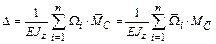 , (5)
, (5)
где  – площадь участка i эпюры M от заданной внешней нагрузки;
– площадь участка i эпюры M от заданной внешней нагрузки;
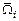 – площадь участка i эпюры
– площадь участка i эпюры 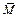 от единичной нагрузки;
от единичной нагрузки;
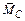 – ордината эпюры
– ордината эпюры 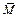 от единичной нагрузки под центром тяжести
от единичной нагрузки под центром тяжести 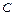 эпюры M на участке i балки;
эпюры M на участке i балки;
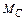 – ордината эпюры M от заданной нагрузки под центром тяжести
– ордината эпюры M от заданной нагрузки под центром тяжести 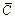 эпюры
эпюры 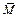 на участке i балки.
на участке i балки.
Правило знаков: если ординаты эпюры M и эпюры 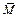 ( формула Симпсона ) или сами эпюры ( формула Верещагина ) расположены по разные стороны от оси расчетной схемы, то результат их умножения имеет знак «минус».
( формула Симпсона ) или сами эпюры ( формула Верещагина ) расположены по разные стороны от оси расчетной схемы, то результат их умножения имеет знак «минус».
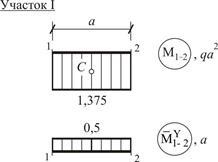
Найдем прогиб 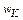 сечения K балки, для чего сначала перемножим по отдельности участки эпюры M (рис. 14) и эпюры
сечения K балки, для чего сначала перемножим по отдельности участки эпюры M (рис. 14) и эпюры 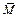 (рис. 23) между одними и теми же контролируемыми сечениями, а затем просуммируем полученные значения. При этом, рассматривая участки I (между сечениями 1–2) и II (между сечениями 3–4), воспользуемся формулой Верещагина (5), а участки III (между сечениями
(рис. 23) между одними и теми же контролируемыми сечениями, а затем просуммируем полученные значения. При этом, рассматривая участки I (между сечениями 1–2) и II (между сечениями 3–4), воспользуемся формулой Верещагина (5), а участки III (между сечениями
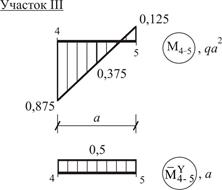
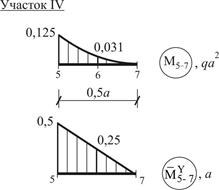
4–5) и IV (между сечениями 5–7) – формулой Симпсона (4), см. рис. 24.
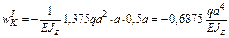
| 

|
| Рис. 24 (начало) | |
| 
|
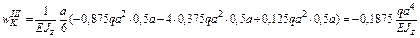
| |
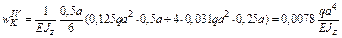
|
Рис. 24 (окончание)
Суммируем полученные значения и найдем прогиб сечения K балки:
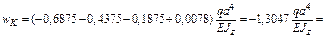
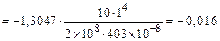 м
м 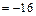 мм,
мм,
здесь 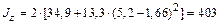 см4
см4 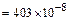 м4 (см. п. 4);
м4 (см. п. 4);
знак “–“ показывает, что прогиб сечения K направлен не вниз (как была направлена сила 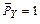 ), а вверх.
), а вверх.
5.4. Построение направляющей эпюры изгибающих моментов от действия единичного изгибающего момента 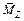 в сечении K.
в сечении K.
5.4.1. Определение опорных реакций.
Заменим опорные связи (рис. 19 б) на опорные реакции (рис. 25), причем одной реакции соответствует один опорный стержень. Реакции до их определения считаются положительно направленными.
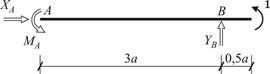
Рис. 25
Найдем неизвестные реакции, используя уравнения равновесия, описанные в п. 2 при определении опорных реакций от заданной нагрузки:
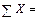
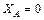 ;
;
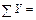
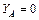 ;
;
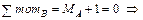
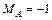 .
.
Заменяя введенные на рис. 25 обозначения реакций найденными векторами, получаем рис. 26 и используем его для проведения контроля правильности определения реакций опорных связей.
Контроль: 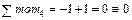 .
.
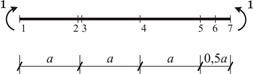
Рис. 26
Количество контролируемых сечений принимается равным числу сечений, назначенных в п. 3.1 для ЗРС (см. рис. 26). Однако для построения направляющейэпюры изгибающих моментов 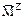 достаточно определить ординаты в сечениях
достаточно определить ординаты в сечениях
1 и 7 (см. п. 3.1), при этом будем иметь один участок с линейным законом изменения изгибающего момента (1–7), см. Приложение 1.
5.4.2. Определение значений ординат и построение направляющейэпюры изгибающих моментов 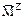 .
.
Найдем значения момента в контролируемых сечениях 1 и 7 (рис. 27).
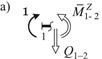
| 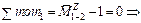
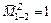 (РВ/Н). (РВ/Н).
|
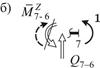 Рис. 27
Рис. 27
| 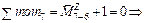
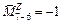 (РВ/Н). (РВ/Н).
|
Полученные данные используем для построения направляющейэпюры изгибающих моментов 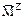 на растянутых волокнах (рис. 28).
на растянутых волокнах (рис. 28).
Значения ординат в оставшихся сечениях 2, 3, 4, 5 и 6 необходимые для дальнейшего расчета легко можно получить, используя эпюру (рис. 28).

Рис. 28
5.5. Определение угла поворота сечения K балки.
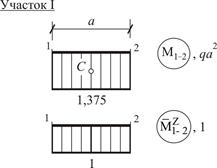
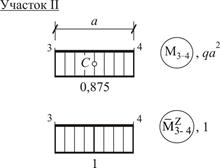
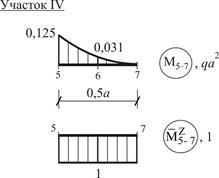
Найдем угол поворота 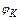 сечения K балки, используя формулу Симпсона и формулу Верещагина также как в п. 5.3. При этом, рассматривая участки I, II и III соответственно между сечениями 1–2, 3–4 и 4–5, воспользуемся формулой Верещагина (5), а участок IV между сечениями 5–7 – формулой Симпсона (4), см. рис. 29.
сечения K балки, используя формулу Симпсона и формулу Верещагина также как в п. 5.3. При этом, рассматривая участки I, II и III соответственно между сечениями 1–2, 3–4 и 4–5, воспользуемся формулой Верещагина (5), а участок IV между сечениями 5–7 – формулой Симпсона (4), см. рис. 29.
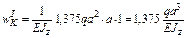
| 
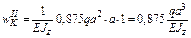
|
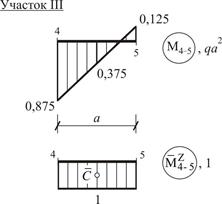
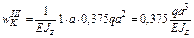
| 
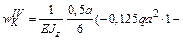
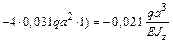
|
Рис. 29
Суммируем полученные значения и найдем угол поворота сечения K балки:
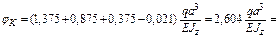
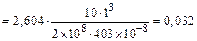 рад,
рад,
знак “+“ показывает, что угол поворота сечения K направлен против часовой стрелки (как был направлен момент 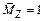 ).
).
5.6. Построение схемы деформирования ЗРС.
Косвенную проверку полученных результатов можно провести, построив деформированное состояние ЗРС по полученным значениям и знакам перемещений сечения K и, сравнив затем полученную картину с деформирующим воздействием приложенных к ЗРС нагрузок.
При построении деформированного состояния нужно учитывать наложенные на ЗРС опорные связи, а также непрерывность и малую величину перемещений точек осей. Схема деформирования, построенная по результатам решения задачи о вычислении перемещений сечения K, представлена на рис. 30.
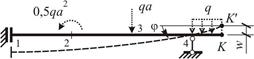
Рис. 30
Анализ поведения ЗРС от действующей нагрузки проводится на основании следующих соображений:
· наличие подвижной заделки в узле 1 при действии сосредоточенной силы 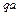 и изгибающего момента
и изгибающего момента 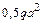 приводит к перемещению этого узла вниз;
приводит к перемещению этого узла вниз;
· наличие шарнирно-подвижной опоры в узле 4 приводит к тому, что данный узел не меняет своего положения, т. е. балка поворачивается относительно этой точки (иначе не сохранить длины участков 1–4 и 4– K);
· свободный от закрепления узел K переместится вверх, и хотя движению вверх препятствует распределенная нагрузка q, однако, ее воздействие в противовес сосредоточенной силе и изгибающему моменту, как показывают полученные результаты, недостаточно;
· в связи с отсутствием нагрузок, действующих вдоль оси балки, пренебрегаем горизонтальными перемещениями узлов балки и опорных связей.
Таким образом, полученные результаты обладают определенной степенью достоверности, как показывает проведенный выше приблизительный анализ деформированного состояния ЗРС.