
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 1.
|
|
Составить математическую модель задачи и решить ее с помощью одного из методов: графическим способом, симплекс-методом (с введением искусственного базиса или без него), системы MAPLE (более высокую оценку получает решение полученное двумя способами). Задача: Звероферма выращивает черно-бурых лисиц и песцов. На
звероферме имеется 10 000 клеток. В одной клетке могут быть либо две лисы, либо 1 песец. По плану на ферме должно быть не менее 3000 лис и 6000 песцов. В одни сутки необходимо выдавать каждой лисе корма - 4 ед., а каждому песцу - 5 ед. Ферма ежедневно может иметь не более 200000 единиц корма. От реализации одной шкурки лисы ферма получает прибыль 10 д.е., а от реализации одной шкурки песца — 5 д. е. Какое количество лисиц и песцов нужно держать на ферме, чтобы получить наибольшую прибыль?
Пусть х1 – количество песцов, х2 – количество лис. Тогда х1 – количество клеток с песцами, х2/2 - количество клеток с лисами, 5*х1 – количество корма для песцов, 4*х2 - количество корма для лис. Составим задачу:
F=5*x1+10*x2 → max,
при ограничениях
x1+x2/2 ≤ 10000, (1)
5*x1+4*x2 ≤ 200000, (2)
x1 ≥ 6000, (3)
x2 ≥ 3000, (4)
x1, x2 ≥ 0.
> with(plots);
> inequal({x1+x2/2< =10000, 5*x1+4*x2< =200000, x1> =6000, x2> =3000, 5*x1+10*x2=0}, x1=-10000..30000, x2=-10000..30000, optionsfeasible=(color=red), optionsexcluded=(color=white)); 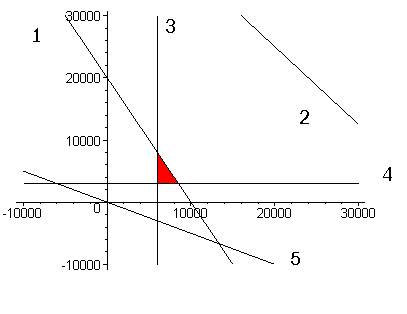
Для решения задачи воспользуемся графическим способом в системе MAPLE (обозначения: 1 – линия x1+x2/2 = 10000, 2 – линия 5*x1+4*x2 = 200000, 3 – линия x1 = 6000, 4 – линия x2 = 3000, 5 – линия grad(F)). Каждое неравенство задает полуплоскость. Их пересечение задает множество дополнительных решений. Чтобы найти максимальной значение целевой функции F=5*x1+10*x2 построим линию уровня 5*x1+10*x2=const(0) и будем двигать ее в направлении градиента. Последняя точка множества дополнительных решений даст максимальное значение целевой функции. Получим точку С = (1)∩ (3). Решим систему уравнений:
x1+x2/2=10000, x2/2=10000-6000, x2=8000,
x1=6000 x1=6000 x1=6000
Проверим правильность решения в системе MAPLE:
> with(simplex);
> maximize(5*x1+10*x2, {x1+x2/2< =10000, 5*x1+4*x2< =200000, x1> =6000, x2> =3000}, NONNEGATIVE);

F(6000; 8000)=5*6000+10*8000=30000+80000=110000.
Проверим в системе MAPLE:
> subs({x1 = 6000, x2 = 8000}, 5*x1+10*x2);

Ответ: Чтобы получить наибольшую прибыль на ферме нужно держать 110000 лис и песцов.