
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 1.3.
|
|
Шаг 1 - Постановка задачи.
Имеется некая производственная фирма, в которой есть отдел технического контроля – ОТК. В этом отделе числятся работники трех разрядов. Известно, что норма выработки за 8-ми часовую смену составляет 2360 изделий, штатное расписание на данный момент – 15 человек. Фирма несет убыток 2$ за каждое бракованное изделие. Требуется составить оптимальное штатное расписание ОТК (минимизация расходов на содержание)
| Разряд | I | II | III |
| Нужное количество работников, не больше | |||
| Средняя производительность в час, n | |||
| Вероятность безотказности изделия, p % | |||
| З/п ($ в час) | 2, 5 | ||
| Таким образом, в нашей модели управляемыми переменными являются количество работников I, II, III разрядов, которых мы должны нанять для выполнения поставленной цели. |
Шаг 2 – ПММ.
2.1. Введем управляемые переменные, с помощью которых мы будем изменять значение ЦФ:
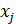 – количество работников j -ого разряда, j =1, 2, 3.
– количество работников j -ого разряда, j =1, 2, 3.
2.2. Наша целевая функция:
f(x1, x2, x3) – общие затраты фирмы на персонал ОТК ($ в час)
f(x1, x2, x3) = (4+2*25*0, 02) x1 + (2, 5+2*20*0, 05) x2 + (2+2*15*0, 08) x3 f(x1, x2, x3) = 5 x1 +4, 5 x2 + 4, 4 x3  (1)
(1)
Выпишем ограничения задачи:
 - ограничение на штатное расписание
- ограничение на штатное расписание 








- ограничение на норму выработки


3 шаг – Анализ модели.
3.1. Для решения поставленной задачи выберем графический метод, потому что данное решение будет выглядеть наглядно.
3.2. Сначала преобразуем модель, т.е. сведем ее к двум переменным.
 (*)
(*)
Тогда














Данную задачу мы решим графическим методом в главе 2, после изложения
графического метода (раздел 2.4).
Здесь же проведем дальнейшее преобразование модели. Для этого ограничение (6) запишем в форме равенства, считая, что мы не будем
перевыполнять норму выработки. Следовательно, выражение (6´) примет вид:
 , или
, или  , откуда
, откуда  , следовательно, можно преобразовать нашу модель (1´)-(7´) к модели с одной переменной.
, следовательно, можно преобразовать нашу модель (1´)-(7´) к модели с одной переменной.
Решение















3.3 Решение задачи (1″)-(7″)
Общее решение, соответствующее неравенствам (2″)-(7″), имеет вид
 .
.
Т.к. нам нужно найти минимальное значение функции, то

 (
( )
)
 (*)
(*)

4, 5, 6 шаги проведем в главе 2.
Пример 1.4. Фабрика выпускает продукцию двух видов: П1 и П2. Продукция обоих видов поступает в оптовую продажу. Для производства этой продукции используются три исходных продукта – A, B, C. Максимально возможные суточные запасы этих продуктов составляют 6, 8 и 5 т соответственно. Расходы сырья A, B, C на 1 тыс. изделий П1 и П2 приведены в
таблице 1.1.
Таблица 1.1
| Исходный продукт | Расход исходных продуктов на 1 тыс. изделий (т) | Максимально возможный запас (т) | |
| П1 | П2 | ||
| A B C | 0, 8 |
Изучение рынка сбыта показало, что суточный спрос на изделия П2 никогда не превышает спроса изделия П1 более чем на 1 тыс. шт. Кроме того, установлено, что спрос на изделия П2 никогда не превышает 2 тыс. шт. в сутки.
Оптовые цены 1 тыс. шт. изделий П1 равны 3 тыс. руб., 1 тыс. шт. П2 – 2 тыс. руб.
Какое количество изделий (в тыс. шт.) каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?
Построение математической модели следует начать с идентификации переменных (искомых величин). После этого целевая функция и ограничения выражаются через соответствующие переменные.
В рассматриваемом примере имеем следующее:
Переменные. Так как нужно определить объемы производства каждого вида продукции, переменными являются:
X1 – суточный объем производства изделия П1 в тыс. шт.;
X2 – суточный объем производства изделия П2 в тыс. шт.
Целевая функция. Так как стоимость 1 тыс. изделий П1 равна 3 тыс. руб., суточный доход от ее продажи составит 3X1 тыс. руб. Аналогично доход от реализации X2 тыс. шт. П2 составит 2X2 тыс. руб. в сутки. При допущении независимости объемов сбыта каждого из изделий общий доход равен сумме
двух слагаемых – дохода от продажи изделий П1 и дохода от продажи изделий П2.
Обозначив доход (в тыс. руб.) через  , можно дать следующую математическую формулировку целевой функции: определить (допустимые) значения X1 и X2, максимизирующие величину общего дохода:
, можно дать следующую математическую формулировку целевой функции: определить (допустимые) значения X1 и X2, максимизирующие величину общего дохода:
 ,
,  .
.
Ограничения. При решении рассматриваемой задачи должны быть учтены ограничения на расход исходных продуктов A, B и С и спрос на изготовляемую продукцию, что можно записать так:
| Расход исходного продукта для производства обоих видов изделий | 
| Максимально возможный запас данного исходного продукта |
Это приводит к трем ограничениям:
X1 + 2X2  6 (для А),
6 (для А),
2X1 + X2  8 (для В),
8 (для В),
X1 + 0, 8X2  5 (для С).
5 (для С).
Ограничения на величину спроса на продукцию имеют вид:
X2 - X1  1 (соотношение величин спроса на изделия П1 и П2),
1 (соотношение величин спроса на изделия П1 и П2),
X2  2 (максимальная величина спроса на изделия П2).
2 (максимальная величина спроса на изделия П2).
Вводятся также условия неотрицательности переменных, т.е. ограничения на их знак:
X1  0 (объем производства П1),
0 (объем производства П1),
X2  0 (объем производства П2).
0 (объем производства П2).
Эти ограничения заключаются в том, что объемы производства продукции не могут принимать отрицательных значений.
Следовательно, математическая модель записывается следующим образом.
Определить суточные объемы производства (Х1 и Х2) изделий П1 и П2 в тыс. шт., при которых достигается
 (целевая функция)
(целевая функция)
при
Х1 + 2Х2  6
6
2X1 + X2  8
8
X1 + 0, 8X2  5
5
-X1 + Х2  1
1
X2  2
2
X1  0, X2
0, X2  0
0
Пример 1.5.
Металлургическому заводу требуется уголь с содержанием фосфора не более 0, 03% и с долей зольных примесей не более 3, 25%. Завод закупает три сорта угля А, В, С с известным содержанием примесей. В какой пропорции нужно смешивать исходные продукты А, В, С, чтобы смесь удовлетворяла ограничениям на содержание примесей и имела минимальную цену?
Содержание примесей и цена исходных продуктов приведены в табл. 1.2.
Таблица 1.2
| Сорт угля | Содержание (%) | Цена 1 т (руб.) | |
| фосфора | золы | ||
| А В С | 0, 06 0, 04 0, 02 | 2, 0 4, 0 3, 0 |
Построим математическую модель. Обозначим:
Х1 – количество угля сорта А в тонне смеси
Х2 – количество угля сорта В в тонне смеси
Х3 – количество угля сорта С в тонне смеси
 – стоимость 1 т смеси – целевая функция,
– стоимость 1 т смеси – целевая функция,
0, 06 Х1 + 0, 04 Х2 + 0, 02 Х3  0, 03 (%) – ограничение на содержание фосфора в смеси,
0, 03 (%) – ограничение на содержание фосфора в смеси,
2 Х1 + 4 Х2 + 3 Х3  3, 25 (%) – ограничение на содержание зольных примесей,
3, 25 (%) – ограничение на содержание зольных примесей,
Х1 + Х2 + Х3 = 1 (т) – ограничение на состав 1 т смеси.
Окончательно математическая модель имеет вид.
Определить количество угля сортов А, В, С (Х1, Х2, Х3) в тонне смеси, при которых достигается

при
0, 06 Х1 + 0, 04 Х2 + 0, 02 Х3  0, 03
0, 03
2 Х1 + 4 Х2 + 3 Х3  3, 25 (1.2)
3, 25 (1.2)
Х1 + Х2 + Х3 = 1
Х1, 2, 3  0.
0.
Пример 1.6. (задача составления кормовой смеси (задача о диете).
Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Недельный расход корма в среднем (за 8 недель) составляет 500 г = 0, 5 кг.
Для того чтобы цыплята достигли к 8-й неделе необходимого веса, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов, или ингредиентов.
В табл. 1.3 приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.
Смесь должна содержать:
не менее 0, 8% кальция
не менее 22% белка от общего веса смеси
не более 5% клетчатки
Требуется определить количество (в кг) каждого из трех ингредиентов, образующих смесь минимальной стоимости, при соблюдении требований к общему расходу кормовой смеси и ее питательности.
Таблица 1.3
| Ингредиент | Содержание питательных веществ | Стоимость (руб./кг) | ||
| (кг/ингредиента) | ||||
| Кальций | Белок | Клетчатка | ||
| Известняк Зерно Соевые бобы | 0, 38 0, 001 0, 002 | - 0, 09 0, 50 | - 0, 02 0, 08 | 0, 4 0, 15 0, 40 |
Математическая формулировка задачи.
Введем следующие обозначения:
Х1 – содержание известняка в смеси (кг);
Х2 – содержание зерна в смеси (кг);
Х3 – содержание соевых бобов в смеси (кг).
Общий вес смеси, еженедельно расходуемый на кормление цыплят:
20 000 ´ 0, 5 = 10 000 кг.
Ограничения, связанные с содержанием кальция, белка и клетчатки в кормовом рационе, имеют вид:
0, 38Х1 + 0, 001Х2 + 0, 002Х3  0, 008 ´ 10 000,
0, 008 ´ 10 000,
0, 09Х2 + 0, 50Х3  0, 22 ´ 10 000,
0, 22 ´ 10 000,
0, 02Х2 + 0, 08Х3  0, 05 ´ 10 000.
0, 05 ´ 10 000.
Окончательный вид математической формулировки задачи:

при ограничениях
Х1 + Х2 + Х3 = 10 000
0.38Х1 + 0.001Х2 + 0.002Х3  80
80
0.09Х2 + 0.50Х3  2200 (1.3)
2200 (1.3)
0.02Х2 + 0.08Х3  500
500
Хj  0, j = 1, 2, 3.
0, j = 1, 2, 3.
Пример 1. 7. (задача о раскрое, или минимизации отходов (обрезков)). Продукция бумажной фирмы выпускается в виде бумажных рулонов стандартной ширины – по
2 метра. По специальным заказам потребителей фирма поставляет рулоны и других размеров, для чего производится разрезание стандартных рулонов. Типичные заказы на рулоны нестандартных размеров приведены в табл. 1.4.
Таблица 1.4
| Заказ | Ширина рулона (м) | Количество рулонов |
| 0, 5 0, 7 0, 9 |
Требуется найти такие сочетания различных вариантов разрезания стандартных рулонов, чтобы поступившие заказы полностью удовлетворить с
минимальными потерями (отходами). Рассмотрим все возможные варианты раскроя стандартного рулона и соответствующие данные сведем в табл. 1.5.
Определим переменные: Хj – количество стандартных рулонов, разрезаемых по варианту j, j = 1, 2, …, 6.
Ограничения непосредственно связаны с требованием обеспечить изготовление требуемого количества нестандартных рулонов. Используя данные табл. 1.5, получим:
Таблица 1.5
| Ширина рулона (м) | Варианты раскроя рулона | Требуемое минимальное количество рулонов | |||||
| 0, 5 0, 7 0, 9 | |||||||
| Отходы (м) | 0, 4 | 0, 3 | 0, 1 | 0, 1 | 0, 2 | - |
2Х2 + 2Х3 + 4Х4 + Х5 = 150 – количество рулонов шириной 0, 5 м,
Х1 + Х2 + 2Х5 = 200 – количество рулонов шириной 0, 7 м,
Х1 + Х3 + 2Х6 = 300 – количество рулонов шириной 0, 9 м.
Выражение для суммарной величины потерь бумаги (отходы) (в м) имеет вид
0, 4Х1 + 0, 3Х2 + 0, 1Х3 + 0, 1Х5 + 0, 2Х6
Таким образом, математическая модель в общем виде:
 = 0, 4X1 + 0, 3X2 + 0, 1X3 + 0, 1X5 + 0, 2X6
= 0, 4X1 + 0, 3X2 + 0, 1X3 + 0, 1X5 + 0, 2X6
при ограничениях:
2X2 + 2X3 + 4X4 + X5 =150
X1 + X2 + 2X5 = 200
X1 + X3 + 2X6 = 300
Xj ≥ 0; Xj – целые; j = 1,..., 6.