
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства полноценного умения решать арифметические задачи
|
|
Рассматривая умение не только как компонент содержания образования, но и как результат обучения, приходим к выводу, что понятие «качество умения» утверждает степень соответствия сформированного в процессе обучения умения тому, каким должно быть умение в зависимости от целей обучения. В соответствии с этим под качеством умения будем понимать обнаруживающуюся в деятельности совокупность его свойств. Полноценным умением будем называть умение, обладающее совокупностью свойств, соответствующих целям обучения [20].
Качество любого умения в содержательных и деятельностных характеристиках отражается в требованиях к нему как ожидаемому результату обучения.
На основе анализа психолого-педагогической литературы и учета того, что у младших школьников лишь закладываются основные понятия, к основным свойствам умения решать арифметические задачи мы отнесли осознанность, самостоятельность, перенос, правильность и прочность [19, 20].
Осознанность умения решать арифметические задачи характеризуется актуальным осознанием в процессе решения задачи математических положений, лежащих в основе выбора арифметического действия (осознанность используемых обосновывающих знаний), и выполняемых операций (осознанность используемых операционных знаний). Проявляется осознанность в том, что в процессе решения задачи ученик актуализирует используемые содержательные и операционные знания.
О сформированности умения решать арифметические задачи можно говорить только в том случае, если ученик без вмешательства со стороны, правильно выполняет всю систему операций, составляющих процесс решения задачи. Это есть проявление такого свойства умения как самостоятельность. Показатель самостоятельности - мера помощи со стороны учителя.
Перенос умения решать арифметические задачи характеризуется проявлением умения в новых условиях.
Если ученик правильно выбирает арифметическое действие, то говорят, что умение решать арифметические задачи обладает правильностью. Для оценки правильности умения используется коэффициент правильности, который определяется отношением числа правильно решенных задач к числу всех задач, предлагаемых для решения.
Если ученик сохраняет сформированное умение в течение длительного времени, то сформированное у него умение обладает прочностью.
Прочность умения рассматривается как сохраняемость осознанности, самостоятельности и правильности.
Прочность правильности умения характеризуется отношением коэффициентов правильности, вычисленных в конце формирования умения (К1) и через некоторый промежуток времени после прекращения функционирования (К2):
Кпр.=  .
.
Правильность обладает высоким уровнем прочности, если указанный коэффициент прочности равен или близок к единице.
Аналогично вычисляются коэффициенты прочности осознанности, самостоятельности умения.
Общие вопросы методики формирования умения решать арифметические задачи
В системе обучения решению арифметических задач необходимо выделить две линии: первая линия - формирование общего умения решать задачи, вторая линия - формирование умения решать задачи каждого вида (типа) на основе общего умения. Под общим умением решать арифметические задачи мы будем понимать овладение системой операций, составляющих процесс решения любой арифметической задачей, а также знаниями о задаче и ее структуре [19, 20].
Работу по формированию общего умения решать задачи целесообразно начать при введении первых арифметических задач, т.е. задач на нахождение суммы и остатка.
В методике обучения решению задач каждого вида (типа) следует предусмотреть следующие ступени:
а) подготовка к введению задач нового вида (типа);
б) ознакомление с решением задач нового вида (типа);
в) формирование умения решать арифметические задачи данного вида (типа) [1].
Рассмотрим основные задачи и методику работы на каждой ступени.
На подготовительной ступени к введению простых арифметических задач ученик должен усвоить теоретическую основу выбора арифметического действия, составных арифметических задач - актуализировать систему теоретических знаний, которые составляют теоретическую основу выбора арифметического действия простых, входящих в неё задач. Необходимо раскрыть новые связи и отношения, которые даются в задаче косвенно (например, два поезда вышли одновременно и встретились через три часа; столько же; по одинаковой цене и т.д.); ознакомить с новыми величинами, которые войдут в содержание задачи; с новыми объектами (комбайн, эскалатор и др.), используя предметные картинки, слайды и т.д. Ученик на этой ступени должен усвоить содержание операций, составляющих процесс решения задач нового вида (типа).
На ступени ознакомления с задачей нового вида (типа) ученик должен усвоить всю систему операций (их последовательность и содержание), составляющих процесс ее решения. В связи с этим на ступени ознакомления учителем используется различная методическая оснастка.
При ознакомлении с содержанием задачи учащиеся после ее прочтения и представления конкретной ситуации, описанной в задаче, выделяют данные и искомое. Существуют дидактические средства, позволяющие ребенку «увидеть» данные и искомое: выделение объектов и чисел, выражающих либо численность множества объектов, либо являющихся значением величин; инсценирование задачи, способствующее осознанию условия и требования задачи (Приглашаются два ученика, одному дается роль условия задачи, второму - вопроса задачи. После прочтения задачи учителем, первый ученик делает шаг вперед и говорит: «Условие задачи:... (повторяет условие задачи)», второй ученик поступает аналогично с вопросом задачи.). Важно научить ребенка правильно повторять задачу, а затем читать: делать логическое ударение на числах и объектах, численность которых обозначают данные числа, на вопросе задачи.
При поиске решения простой арифметической задачи ученик выполняет операции 3-5; составной арифметической задачи - 3. Это центральный момент по решению задачи. Главная цель учителя так организовать работу детей, использовать такие методические приемы и средства, чтобы научить ученика самостоятельному нахождению решения задачи.
Большую помощь в этом оказывает иллюстрация задачи, которая должна стать «средством ученика». Умению иллюстрировать задачу нужно целенаправленно обучать.
Виды иллюстраций, используемых в традиционной начальной школе:
1) Непосредственная (сами предметы, о которых идет речь в задаче), образная (рисунки тех предметов, о которых идет речь в задаче). Часто иллюстрации сопровождаются числовыми надписями.
Эти виды иллюстраций применяются при решении простых арифметических задач в первом и втором классах в начале ступени ознакомления с задачей нового вида.
2) Чертежи.
Чаще всего выполняются с использованием отрезков, которые выражают количественные отношения. Программой предусматривается использование чертежей при решении задач со второго класса. Используется такой вид иллюстрации в практике работы школы, к сожалению, явно недостаточно.
3) Краткая запись задачи.
Нет установленного образца её выполнения, форма краткой записи задачи диктуется целесообразностью, удобством. Выполняется в любой форме, лишь бы она помогала установлению связей между данными и искомым или между данными. Числа записываются с наименованиями, словами или отдельными буквами обозначаются объекты. Отношения «больше», «меньше» могут указываться стрелками, которые обозначают численность каких множеств (или значения величин) находятся в данном отношении. Сами слова «больше», «меньше» можно заменять одной буквой и для отличия от наименований подчёркивать. Обозначать отношения «больше», «меньше» знаками «>», «<» в краткой записи задачи ни в коем случае нельзя: это не стенографические знаки, а знаки бинарных отношений, которые ставятся между двумя математическим выражениями (а> d, 4< 5, а+в> 3+х и т.д.).
Примеры:

 1) К. - 8 яб.
1) К. - 8 яб.
 С. -? яб., на 2 яб. м.
С. -? яб., на 2 яб. м.
или
2) К. - 8 яб.
С. -? яб., на 2 яб. м.
На наш взгляд, вариант 2 целесообразнее, так как в задаче речь идёт о двух объектах и без стрелок вполне очевидно, численности каких множеств сравнивается.
В тех случаях, когда в краткой записи трудно обозначить искомое вопросительным знаком, требование задачи записывается полностью.
Не каждую задачу нужно иллюстрировать. Иллюстрация должна быть помощником, а не материалом, за которую ставится отметка. Но учить иллюстрации необходимо. На этапе ознакомления с задачей нового вида (типа) это должно быть предметом специального усвоения.
Краткая запись, как вид иллюстрации задачи, используется во всех начальных классах для решения составных и реже - простых арифметических задач.
4) Особая трудность возникает при обучении решению первых простых арифметических задач у первоклассников.
В методической литературе рекомендуется при обучении первоклассников решению простых арифметических задач использовать предметные или образные иллюстрации и схематические (в виде краткой записи или чертежа). Предметная иллюстрация, безусловно, помогает создать яркое представление той жизненной ситуации, которая описывается в задаче, что в дальнейшем служит отправным моментом для выбора арифметического действия. Однако, она имеет ряд недостатков: она не изображает наглядно объект усвоения - связь между данными и искомым, не помогает абстрагироваться от конкретной ситуации задачи и выделить существенно общее для всех задач каждого вида - связь между данными и искомым, её использование ограничено (особенно при самостоятельном решении), чаще всего она является «средством учителя», а не «средством самого ученика».
В связи с этим предметную иллюстрацию целесообразно использовать только при ознакомлении с решением простых арифметических задач.
Схематическая наглядность в виде краткой записи или чертежа имеет ряд преимуществ перед предметной или образной наглядностью, но затрудняет учеников, так как требует умения писать и чертить, что должно стать предметом специального усвоения. Следовательно, использовать её с первых дней обучения ребёнка школе сложно.
Учитывая это, при обучении первоклассников решению простых арифметических задач мы считаем целесообразным использовать иллюстрацию в виде «картинки с точками».
При решении простых арифметических задач объектом усвоения является не та ситуация, которая описана в задаче, а те связи, которые существуют между данными или между данными и искомым. Разнообразие конкретных предметов и сюжетов в задачах не позволяет детям выделить и осознать эти связи при использовании предметной наглядности. Для того чтобы помочь детям выполнению этих операций при решении задачи, мы поступили следующим образом [17].
Каждый конкретный предмет, о котором идёт речь в задаче, мы обозначили точкой, что позволило абстрагироваться от всех свойств объектов в задаче. С помощью схем мы изобразили и связи между объектами, т.е. операции над множествами.
Так модель ситуации, описанной в задаче: «С аэродрома улетело сначала 6 самолётов, а потом ещё 2 самолёта. Сколько всего самолётов улетело с аэродрома?», будет иметь вид:
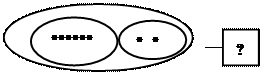
Модель ситуации, описанной в задаче: «В гараже было 6 машин, 2 машины уехали. Сколько машин осталось в гараже?», будет иметь вид:


Как видим, иллюстрации помогают ученику, конкретизируя ситуацию, описанную в задаче, в то же время абстрагироваться от неё, выделить и актуально осознать, «увидеть» связи между данными и искомым. Кроме того, она указывает способ организации деятельности ребёнка, направленной на выявление объекта усвоения. Эти иллюстрации просты в исполнении, поэтому ребёнок может научиться выполнять их с первого дня обучения в школе, раскрывая в процессе практических действий связи между данными и искомым.
Иллюстрации в виде «картинок с точками» целесообразно использовать на этапах подготовки и ознакомления с простыми арифметическими задачами, теоретической основой выбора арифметического действия в которых является конкретный смысл арифметических действий. Выполнять иллюстрации можно в блокноте для рисования. До того момента, пока дети не умеют писать, решение либо проговаривается устно, либо записывается на наборном полотне с помощью разрезных цифр.
Как показало проведённое исследование, все дети, правильно выполнившие иллюстрацию, правильно выбрали арифметическое действие даже в задачах с усложнённым конкретным содержанием и усложнённой структурой текста. Кроме того, они смогли обосновать выбор арифметического действия.
Замечено, что использование при решении задач «картинок с точками» резко повышает интерес к этой деятельности, делает её одной из самых привлекательных для ребёнка.
Не менее важным средством, помогающим ученику осуществить поиск решения задачи, является разбор задачи.
Методисты выделяют два вида разбора:
1) Разбор по существу, представляющий собою беседу, позволяющую ученику раскрыть проблему задачи, или, словами В.Оконь, «развязать трудный узел» [15].
Например, задача на нахождение неизвестного по двум разностям: «Купили по одинаковой цене 10 м шерсти и 14 м полотна, за полотно заплатили на 200 р. больше, чем за всю шерсть. Сколько уплатили за всё полотно и за всю шерсть в отдельности?»
Трудный узел: установить, что 200 р. уплатили за полотно, купленное сверх 10 м.
Учитель ставит вопросы:
- За сколько метров полотна уплатили столько же, сколько за всю шерсть? (За 10 м.)
- За какое полотно уплатили 200 р.? (За полотно, купленное сверх 10 м, уплатили 200 р.)
- Следовательно, 200 р. - это стоимость какого полотна?
(200 р. - это стоимость полотна, купленного сверх 10 м.)
- Если мы знаем стоимость полотна и будем знать его количество, то, что мы сможем узнать по этим данным? (Зная стоимость полотна и его количество, можно узнать цену полотна.)
Дальше переходят к формальному разбору от числовых данных. Об этом виде разбора речь пойдёт далее.
2) Формальный разбор, представляющий собою беседу, выполняемую по определённой схеме. Он позволяет выделить две системы операций: над числами и объектами задачи. Заканчивается он составлением плана решения задачи.
Выделяют два вида формального разбора: разбор от вопроса к числовым данным; разбор от данных к вопросу.
Чтобы научить школьника самостоятельно осуществлять поиск решения задачи, методисты разрабатывают «памятки» по решению задач, которые отображают систему операций по её решению. Этими памятками дети пользуются в процессе решения задач сначала с помощью и под руководством учителя, а затем самостоятельно.
При обучении решению простых арифметических задач можно использовать следующие памятки [18]:
а) При решении первых простых арифметических задач:
Рассуждаю так:
1. Мне известно...
2. Надо узнать...
3. Рисую и объясняю...
4. Подумаю, надо объединять или удалять...
5. Подумаю, надо прибавлять или вычитать...
6. Выполняю решение...
7. Отвечаю на вопрос задачи...
б) При решении различных видов простых арифметических задач:
Рассуждаю так:
1. Мне известно...
2. Надо узнать...
3. Запишу задачу кратко...
4. Подумаю, большее или меньшее число надо находить...
5. Подумаю, каким действием...
6. Выполняю решение...
7. Отвечаю на вопрос задачи...
8. Проверяю...
При обучении решению составных арифметических задач считаем целесообразным использовать два вида памяток:
1) Разбор от вопроса к числовым данным.
Рассуждаю так:
1. Мне известно...
2. Надо узнать...
3. Запишу задачу кратко...
4. Подумаю, что нужно знать, чтобы ответить на вопрос задачи...
5. Каким действием?
6. Подумаю, могу ли сразу ответить на вопрос задачи?
Почему?
(Операции 4-6 выполняются столько раз, сколько арифметических действий в задаче.)
7. Составляю план решения.
8. Выполняю решение.
9. Отвечаю на вопрос задачи.
10. Проверяю.
2)Разбор от числовых данных к вопросу.
Рассуждаю так:
1. Мне известно...
2. Надо узнать...
3. Запишу кратко задачу...
4. Выделяю два данных числа...
5. Подумаю, что можно узнать по этим данным...
6. Каким действием?
(Операции 4-6 выполняются столько раз, сколько арифметических действий в задаче.)
7. Составляю план решения...
8. Выполняю решение...
9. Отвечаю на вопрос задачи...
10. Проверяю.
Кроме памяток, являющихся вербальными моделями способов деятельности по решению составных арифметических задач, мы сочли необходимым при обучении детей этой возрастной группы решению данных задач использовать схематическую модель способа деятельности по решению составной арифметической задачи, так называемую «схему размышления». Она отображает в наглядной форме всю последовательность операций, выполняемых при решении составной арифметической задачи. Приведём примеры полного рассуждения ученика при разборе задачи от вопроса к числовым данным и от числовых данных к вопросу с использованием схем размышления.
Задача. Во дворе играли 5 девочек и 4 мальчика. Сколько детей осталось играть во дворе, если 6 детей ушло?
1) Полное рассуждение ученика при разборе от вопроса к числовым данным.
1. Мне известно, что играли во дворе 5 девочек, 4 мальчика и что 6 детей ушли.
2. Надо узнать, сколько детей осталось играть во дворе.
3. Запишу задачу кратко.
В задаче главные слова: играли, ушли, осталось.
Играли - 5 дев. и 4 мал.
Ушли - 6 дет.
Осталось -? дет.
Главный вопрос задачи подчёркиваю.
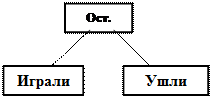
4. Чтобы узнать, сколько детей осталось играть, надо знать, сколько детей играли и сколько детей ушли.
(Изображает часть схемы:
 ?
?
).
5. Если я буду знать, сколько всего детей играло и сколько ушло, то смогу узнать, сколько осталось играть действием вычитания (ставит в схеме знак «-»).
6. Сразу узнать, сколько детей осталось играть, я не могу, потому что не знаю, сколько всего детей играло (ставит в схеме около «Играли» знак вопроса).
4а. Чтобы узнать, сколько всего детей играло во дворе, надо знать, сколько играло мальчиков и сколько девочек (изображает в схеме).
5а. Если я буду знать, сколько играло девочек и сколько мальчиков, то смогу узнать, сколько всего детей играло действием сложения (ставит в схеме знак «+»).
6а. Я могу сразу узнать, сколько всего детей играло, потому что знаю, что девочек играло 5, мальчиков - 4.
7. Составляю план решения. Сначала действием сложения узнаю, сколько всего детей играло, потом действием вычитания узнаю, сколько детей осталось играть (ставит в схеме соответственно цифры 1 и 2 над знаками действий).
Схема приобретает вид:
 ?
?
? 2
-
+ +
(О2 — АД2 — О1 — АД1 — АД1 — АД2)
2) Разбор от числовых данных к вопросу.
Выполним только операции, начиная с 4.
4. Знаю, что девочек было 5, мальчиков 4.
5. Могу узнать, сколько играло всего детей.
6. Действием сложения.
4а. Буду знать, сколько всего играло и знаю, что 6 детей ушли.
5а. Смогу узнать, сколько детей осталось играть, отвечу на главный вопрос задачи.
6а. Действием вычитания.
Одновременно также можно выполнить схему, отображающую процесс поиска решения задачи:
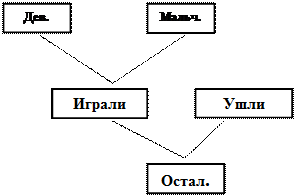 |
+
-
В методической литературе даются всевозможные памятки, но, на наш взгляд, они не отображают полностью деятельность ребёнка по решению задачи, т.е. не являются моделью этой деятельности. Поэтому их использование не обеспечивает требуемой эффективности процесса обучения решению задач.