Кривые конических сечений

При сечении прямого кругового конуса плоскостями, различно расположенными относительно оси конуса, получаются контуры сечения, образующие эллипс, параболу и гиперболу.

При пересечении плоскостью P_V всех образующих конуса получается эллипс (рис. 72, а и б)

При пересечении конуса плоскостью P_V, параллельной одной из образующих конуса (рис. 72. в) получается парабола (рис. 72, г).

При пересечении конуса плоскостью P _V параллельной оси конуса, получается гипербола (рис. 72, д и е).

Эллипс – замкнутая плоская кривая, сумма расстояний каждой точки которой до двух данных точек (фокусов), лежащих на большой оси, есть величина постоянная и равная длине большой оси.

Широко применяемый в технике способ построения эллипса по большой (АВ) и малой (CD) осям представлен на рис. 72, б.

Проводят две перпендикулярные осевые линии. Затем от центра О откладывают вверх и вниз по вертикальной оси отрезки, равные длине малой полуоси, а влево и вправо по горизонтальной оси – отрезки, равные длине большой полуоси.

Из центра О радиусами ОА и ОС проводят две концентрические окружности и ряд лучей-диаметров. Из точек пересечения лучей с окружностями проводят линии, параллельные осям эллипса, до взаимного пересечения в точках, принадлежащих эллипсу. Полученные точки соединяют от руки и обводят по лекалу.

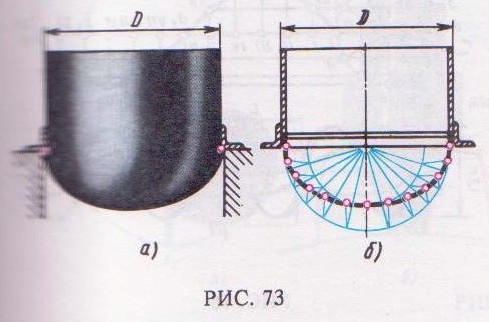
На рис. 73, а показан резервуар, контурное очертание днища которого имеет форму эллипса.

Построение очертания днища (половины эллипса приведено на рис. 73, б. Большой осью эллипса является диаметр D цилиндрической части резервуара, а малой полуосью эллипса – наибольшее расстояние по вертикали от большой оси до днища.

Парабола – плоская кривая, каждая точка которой равноудалена от директрисы DD ₁, прямой, перпендикулярной к оси симметрии параболы, и от фокуса F – точки, расположенной на оси симметрии параболы (см. рис. 72, г).

Расстояние KF между директрисой и фокусом называется параметром р параболы. Точка О, лежащая на оси симметрии, называется вершиной параболы и делит параметр р пополам.

Для построения параболы по заданной величине параметра р проводят ось симметрии параболы и откладывают отрезок KF = р. Через точку К

перпендикулярно оси симметрии проводят дирек­трису DD ₁. Отрезок KF делят пополам и получают вершину О параболы. От вершины О вниз на

оси симметрии намечают ряд произвольных точек I–VI с постепенно увеличивающимся расстоянием между ними. Через эти точки проводят вспомогательные прямые, перпендикулярные оси симметрии. На вспомогательных прямых из фокуса F делают засечки радиусом, равным расстоянию от прямой до директрисы. Например, из точки F на вспомогательной прямой, проходящей через точки V, делают засечку дугой
R ₁ = KV; полученная точка 5 принадлежит параболе.

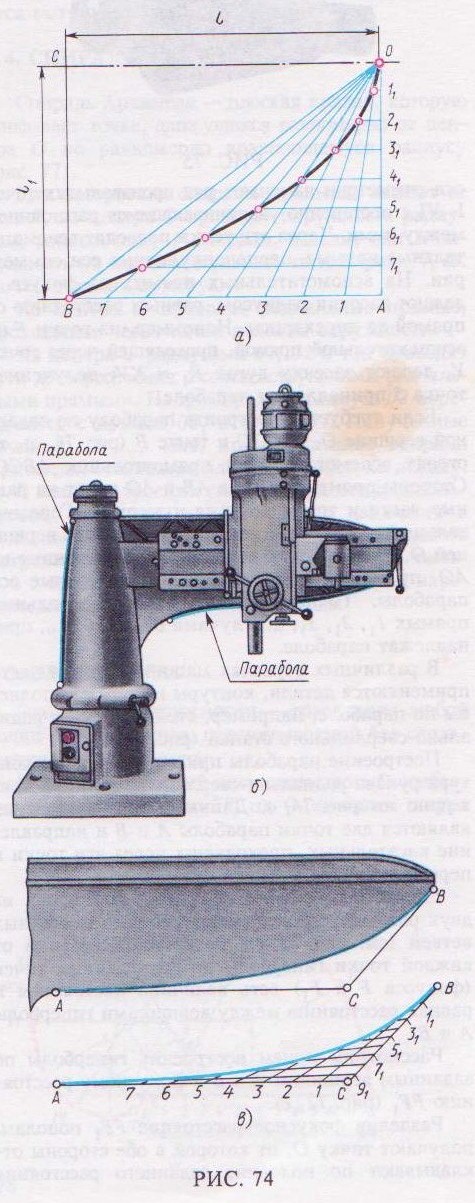
Если требуется построить параболу по задан­ной вершине О, оси ОС и точке В (рис. 74, а), то строят вспомогательный прямоугольник АВСО. Стороны прямоугольника АВ и АО делят на рав­ные части и точки деления нумеруют. Горизон­тальный ряд делений соединяют лучами с вершиной О, а через точки делений, расположенные на АО, проводят прямые линии, параллельные оси параболы. Точки пересечения горизонтальных прямых 1₁, 2 ₁, 3 ₁,... с лучами 01, 02, 03,... принадлежат параболе.

В различных отраслях машиностроения часто применяются детали, контуры которых выполнены по параболе, например, стойка и рукав радиально-сверлильного станка (рис. 74, б).

Построение параболы при вычерчивании контура рукава радиально-сверлильного станка приведено на рис. 74, в. Данными для построения являются две точки параболы А и В и направление касательных, проходящих через эти точки и пересекающихся в точке С.

Гипербола – плоская кривая, состоящая из двух разомкнутых, симметрично расположенных ветвей (см. рис. 72, е). Разность расстояний от каждой точки гиперболы до двух данных точек (фокусов F и F ₁) есть величина постоянная и равная расстоянию между вершинами гиперболы А и В.

Рассмотрим прием построения гиперболы по заданным вершинам А и В ифокусному расстоя­нию FF ₁(рис. 72, е).

Разделив фокусное расстояние FF ₁пополам, получают точку О, от которой в обе стороны от­кладывают по половине заданного расстояния

между вершинами А и В. Вниз от фокуса F намечают ряд произвольных точек 1, 2, 3, 4... с постепенно увеличивающимся расстоянием между ними. Из фокуса F описывают дугу вспомогательной окружности радиусом R, равным, например, расстоянию от вершины гиперболы В до точки 3. Из фокуса F ₁проводят вторую дугу вспомогательной окружности радиусом r, равным расстоянию от вершины А до точки 3. На пересечении этих дуг находят точки С и C ₁, принадлежащие гиперболе. Таким же способом находят остальные точки гиперболы.

Вторую ветвь гиперболы строят аналогичным образом.

На рис. 75 показана деталь " проушина", на боковой поверхности которой имеется линия, представляющая собой гиперболу.