Изометрическая проекция окружности

На рис. 139 изображена изометрическая проек­ция куба с окружностями, вписанными в его гра­ни. Квадратные грани куба будут изображаться в виде ромбов, а окружности в виде эллипсов. Наде запомнить, что малая ось CD каждого эллипса всегда должна быть перпендикулярна большой оси АВ.

Если окружность расположена в плоскости, параллельной плоскости Н, то большая ось АВ должна быть перпендикулярна оси z, а малая ось CD – параллельна оси z (рис. 139).

Если окружность расположена в плоскости, параллельной плоскости V, то большая ось эллип­са должна быть проведена под углом 90° к оси y.

При расположении окружности в плоскости, параллельной плоскости W, большая ось эллипса располагается под углом 90° к оси х.

Заметим, что большие оси всех трех эллипсов направлены по большим диагоналям ромбов.

При построении изометрической проекции ок­ружности без сокращения по осям х, у и z длина большой оси эллипсов берется равной 1, 22 диа­метра d изображаемой окружности, а длина малой оси эллипса – 0, 71 d (рис. 139).

В учебных чертежах вместо эллипсов рекомен­дуется применять овалы, очерченные дугами окружностей. Упрощенный способ построения ова­лов приведен на рис. 140.

Для построения овала соответствующей изомет­рической проекции окружности, параллельной плоскости Н, проводят вертикальную и горизон­тальную оси овала (рис. 140, а). Из точки пересе­чения осей О проводят вспомогательную окруж­ность диаметром d, равным действительной величине диаметра изображаемой окружности, и находят точки n₁, n₂, n₃, n₄ пересечения этой окруж­ности с аксонометрическими осями х и у. Из точек т ₁ и т ₂ пересечения вспомогательной окружности с осью z, как из центров радиусом R = m₁n₃, проводят две дуги 23 и 14, принадлежащие овалу. Пересечения этих дуг с осью z дают точки С и D.

Из центра О радиусом ОС, равным половине малой оси овала, засекают на большой оси овала АВ точки О₁ и О ₂- Точки 1, 2, 3 и 4 сопряжений

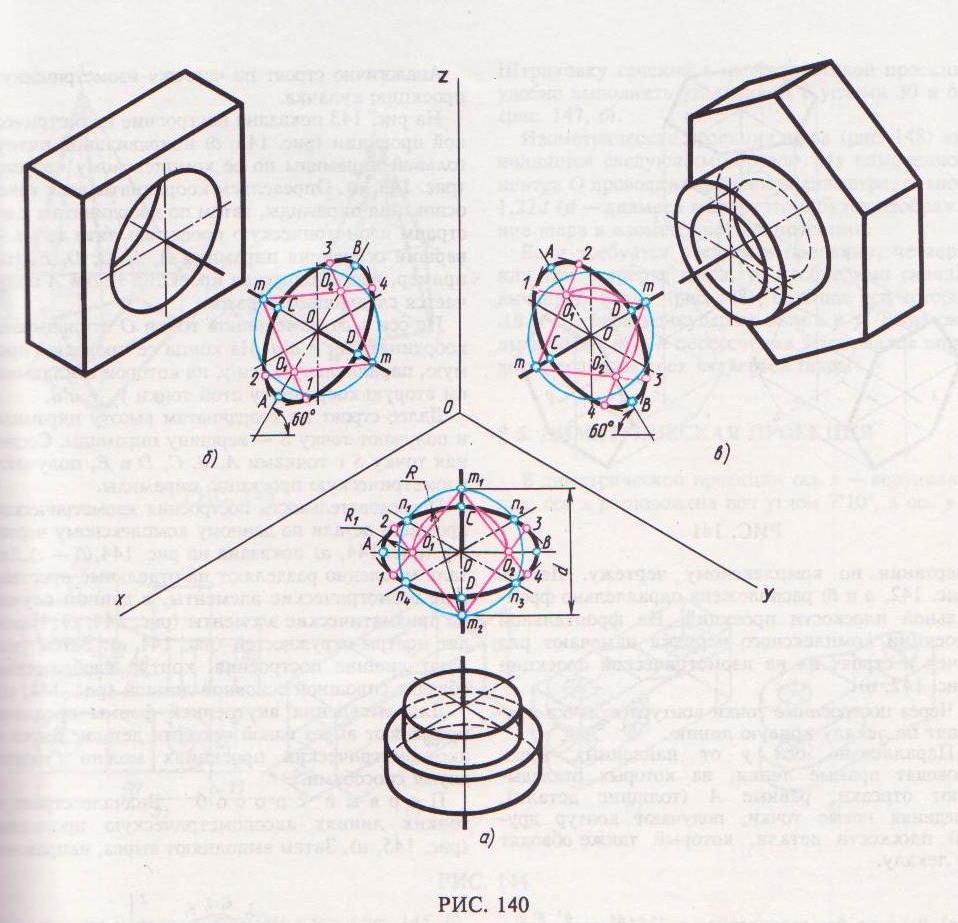
дуг радиусов R и R₁ находят, соединяя точки т₁ и т₂ с точками О₁ и О₂ и продолжая прямые до пересечения с дугами 23 и 14. Из точек О₁ и О₂ радиусом R₁=О₁ 1 проводят две дуги.

§4. ИЗОМЕТРИЧЕСКИЕ ПРОЕКЦИИ

ГЕОМЕТРИЧЕСКИХ ТЕЛ

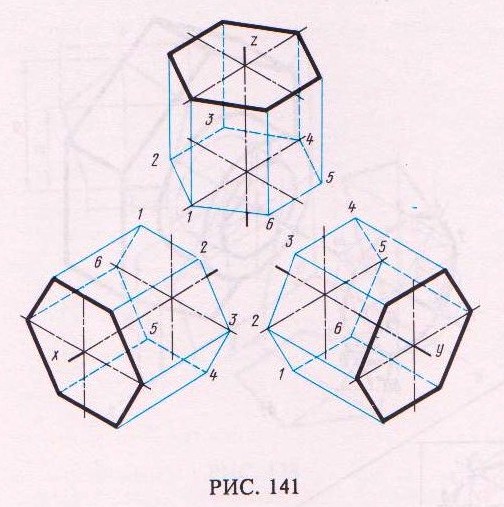
Изображение геометрического тела в изометрической проекции, например правильной шестиугольной призмы, выполняют в такой последовательности (рис. 141).

Если основные призмы – правильный многоугольник (например, шестиугольник), то построение вершин основания по координатам можно упростить, проведя одну из осей коор-

динат через центр основания. На рис. 141 оси х, у и z проведе­ны через центры правильных шестиугольников призмы.

Построив изометрическую проекцию основания призмы, из вершин шестиугольника основания проводим прямые, параллельные соответственно осям х, у или z (для каждой из рассматриваемых на рис. 141 призм). На этих прямых от вершин основания отложим высоту призмы и получим точки 1, 2, 3, 4, 5, 6 вершин другого основания призмы. Соединив эти точки прямыми, получим изометрическую проекцию призмы. В заключение устанавливаем видимые и невидимые линии; не­видимые линии надо проводить штриховыми ли­ниями.

На рис. 142 показано построение изометричес­кой проекции плоской детали криволинейного

очертания по комплексному чертежу. Деталь (рис. 142, а и б) расположена параллельно фрон­тальной плоскости проекций. На фронтальной проекции комплексного чертежа намечают ряд точек и строят их на изометрической проекции (рис. 142, в).

Через построенные точки контура кулачка про­водят по лекалу кривую линию.

Параллельно оси у от найденных точек проводят прямые линии, на которых отклады­вают отрезки, равные А (толщине детали). Соединяя новые точки, получают контур дру­гой плоскости детали, который также обводят по лекалу.

Аналогично строят по чертежу изометрическую проекцию кулачка.

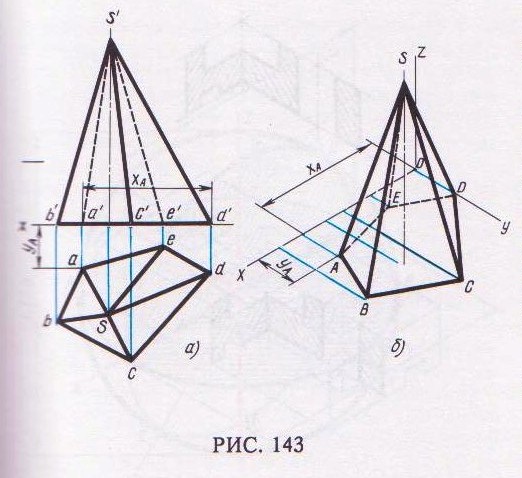
На рис. 143 показано построение изометричес­кой проекции (рис. 143, б) неправильной пятиу­гольной пирамиды по ее комплексному чертежу (рис. 143, а). Определяем координаты всех точек основания пирамиды, затем по координатам х и у строим изометрическую проекцию пяти точек – вершин основания пирамиды А, В, С, D, Е. На­пример, изометрическая проекция точки А полу­чается следующим образом.

По оси х от намеченной точки О откладываем координату х_А = a'd. Из конца ее проводим пря­мую, параллельную оси у, на которой откладыва­ем вторую координату этой точки у_А = a'd.

Далее строят по координатам высоту пирамиды и получают точку S – вершину пирамиды. Соеди­няя точку S с точками А, В, С, D и Е, получают изометрическую проекцию пирамиды.

Последовательность построения изометрической проекции детали по данному комплексному черте­жу (рис. 144, а) показана на рис. 144, (б – г).Деталь мысленно разделяют на отдельные простей­шие геометрические элементы, в данном случае на призматические элементы (рис. 144, б). Нахо­дят центры окружностей (рис. 144, в). Затем уда­ляют лишние построения, контур изображения обводят сплошной основной линией (рис. 144, г).

Для выявления внутренней формы предмета применяют вырез одной четверти детали. Вырез е аксонометрических проекциях можно строил двумя способами.

Первый способ. Вначале строят в тонких линиях аксонометрическую проекцию (рис. 145, а). Затем выполняют вырез, направляя

Штриховку сечений в изометрической проекции удобно выполнять угольником с углами 30 и 60° (рис. 147, б).

Изометрическая проекция шара (рис. 148) вы­полняется следующим образом. Из намеченного центра О проводят окружность диаметра, равного 1.22 d(d – диаметр шара); это и будет изображе­ние шара в изометрической проекции.

Если требуется построить половину, четверть или три четверти шара, то необходимо сначала вычертить овалы (рис. 148), большие оси которых АВ и CD перпендикулярны осям z и у. Тогда ова­лы и точки т и п пересечения этих овалов опре­делят границы трех четвертей шара.