
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формы геометрических тел
|
|
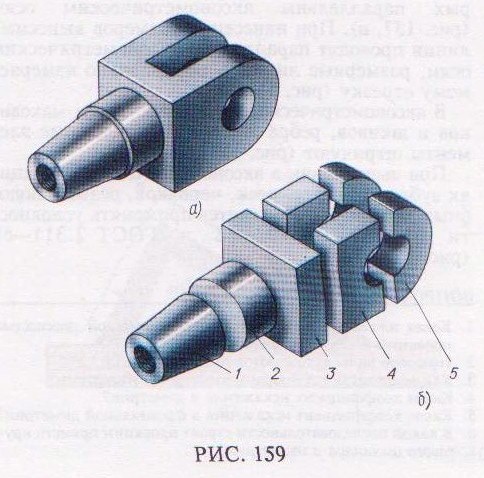
Деталь любой формы можно представить как совокупность отдельных геометрических тел.
Для примера возьмем деталь (рис. 159, а) и проанализируем ее форму. Мысленно разделив ее на отдельные элементы, получим следующие геометрические тела (рис. 159, б): 1 – усеченный прямой круговой конус с цилиндрическим отверстием, 2 – прямой круговой цилиндр, 3 – прямоугольный параллелепипед, 4 – два прямоугольных параллелепипеда с цилиндрическими отверстиями, 5 – два полых полуцилиндра. Для выполнения комплексных чертежей необходимо усвоить методы проецирования отдельных геометрических тел, а также точек и линий, расположенных на поверхности этих тел.
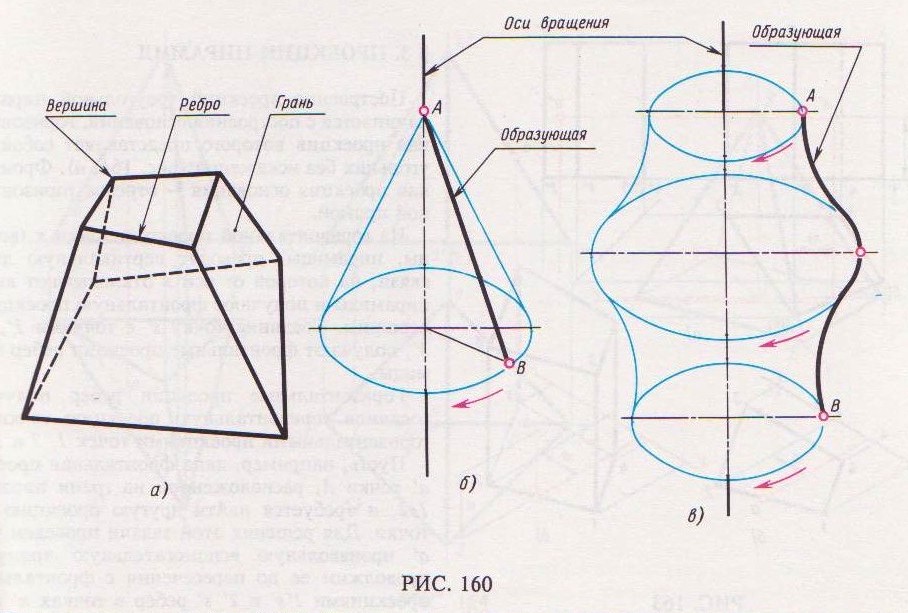
Геометрические тела, ограниченные плоскими многоугольниками, называются многогранниками (рис. 160, а).Эти многоугольники называются гранями, их пересечения – ребрами. Угол, образованный гранями, сходящимися в одной точке – вершине, называется многогранным углом.
Тела вращения ограничены поверхностями, которые получаются в результате вращения какой-либо линии вокруг неподвижной оси (рис. 160, б и в). Линия АВ, которая при своем движении образует поверхность, называется образующей. Наиболее часто встречаются такие тела вращения, как цилиндр, конус, шар, тор.
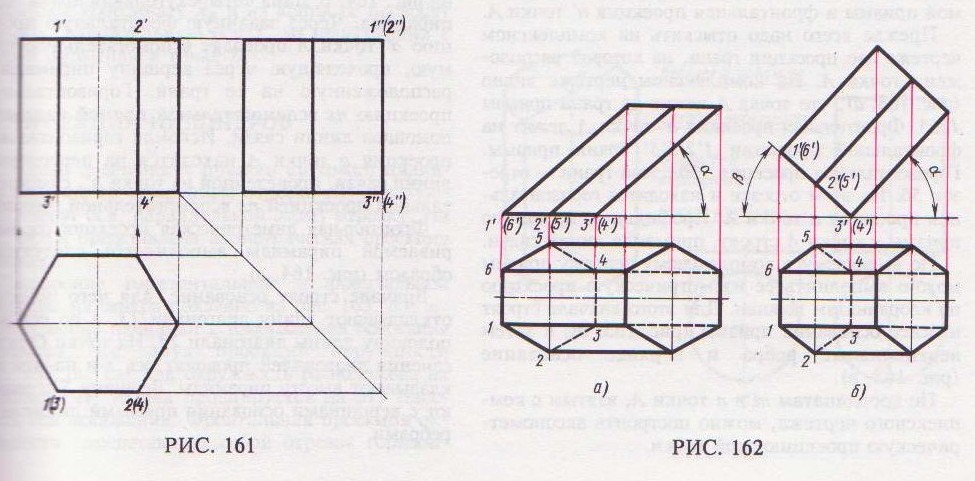
§ 2. ПРОЕКЦИИ ПРИЗМ
Построение проекций правильной прямой шестиугольной призмы (рис. 161 ) начинается с выполнения ее горизонтальной проекции – правильного шестиугольника. Из вершин этого шестиугольника проводят вертикальные линии связи и строят фронтальную проекцию нижнего основания призмы. Эта проекция изображается отрезком горизонтальной прямой. От этой прямой вверх откладывают высоту призмы и строят фронтальную проекцию верхнего основания. Затем вычерчивают фронтальные проекции ребер – отрезки вертикальных прямых, равные высоте призмы. Фронтальные проекции передних и задних ребер совпадают. Горизонтальные проекции боковых граней изображаются в виде отрезков прямых. Передняя боковая грань 1243 изображается на плоскости V без искажения, а на плоскости W – в виде прямой линии. Фронтальные и профильные проекции остальных боковых граней изображаются с искажением.
На чертеже оси х, у и z не показывают, что делает чертеж более простым.
Несколько сложнее построение проекций наклонной призмы.
Рассмотрим порядок построения проекций наклонной шестиугольной призмы.
1. Призма, основание которой лежит на плоскости Н, наклонена к этой плоскости под углом α (рис. 162, а). Ребра призмы параллельны плоскости V, т.е. являются фронталями.
Вначале выполняется построение горизонтальной проекции основания призмы, которое проецируется на плоскость Н без искажения (правильный шестиугольник). Фронтальная проекция основания представляет собой отрезок прямой, параллельной оси х.
Из точек 1 ', 2 ', 3' фронтальной проекции основания проводят прямые проекции ребер под углом α к оси х и на них откладывают действительную длину бокового ребра призмы.
Строят фронтальную проекцию верхнего основания призмы в виде отрезка прямой, равного и параллельного фронтальной проекции нижнего основания.
Из точек 1, 2, 3, 4, 5, 6 горизонтальной проекции нижнего основания проводят прямые – проекции ребер – параллельно оси х и на них с помощью вертикальных линий связи находят шесть точек – горизонтальные проекции вершин верхнего основания призмы.
2. Прямая правильная шестиугольная призма наклонена под углом α к плоскости Н. Основание призмы наклонено к плоскости Н под углом β (рис. 162, б).
В этом случае необходимо вначале построить фронтальную проекцию основания. Эта проекция представляет собой отрезок, равный расстоянию между параллельными сторонами шестиугольника. Если этот отрезок разделить пополам и из его
середины провести линию связи, то на ней будут расположены точки 2 и 5 – горизонтальные проекции вершин основания призмы. Расстояние между точками 2, 5 равно действительному расстоянию между вершинами основания призмы. Так как горизонтальные проекции сторон 16 и 34 представляют собой их действительные длины, то, воспользовавшись этим обстоятельством, можно построить полностью горизонтальную проекцию основания.
Дальнейший процесс построения, показанный на рис. 162, б, аналогичен приведенному на рис. 162, а.
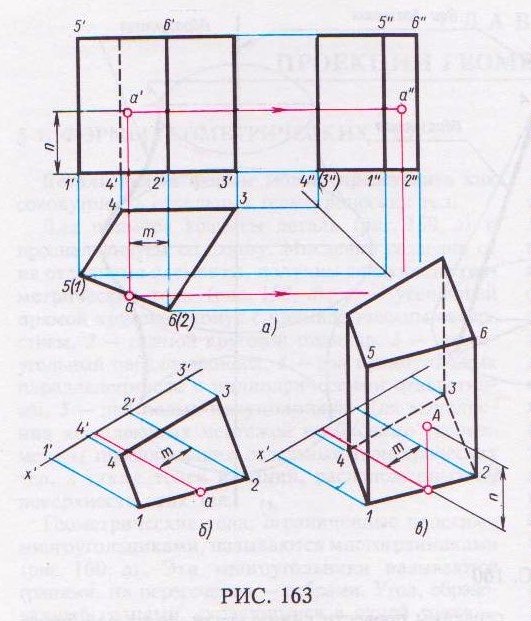
На комплексных чертежах предметов часто приходится строить проекции линий и точек, расположенных на поверхности этих тел, имея только одну проекцию линии или точки. Рассмотрим решение такой задачи.
Дан комплексный чертеж четырехугольной прямой призмы и фронтальная проекция а' точки А.
Прежде всего надо отыскать на комплексном чертеже две проекции грани, на которой расположена точка А. На комплексном чертеже видно (рис. 163, а), что точка А лежит на грани призмы 1265. Фронтальная проекция а' точки А лежит на фронтальной проекции 1'2'6'5' грани призмы. Горизонтальная проекция 1562 этой грани – отрезок 56. На этом отрезке и находится горизонтальная проекция а точки А. Профильную проекцию призмы и точки А строят, применяя линии связи.
По имеющемуся комплексному чертежу призмы можно выполнить ее изометрическую проекцию по координатам вершин. Для этого вначале строят нижнее основание призмы (рис. 163, б), а затем вертикальные ребра и верхнее основание (рис. 163, в).
По координатам т и п точки А, взятым с комплексного чертежа, можно построить аксонометрическую проекцию этой точки.