
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проекции кольца и тора
|
|
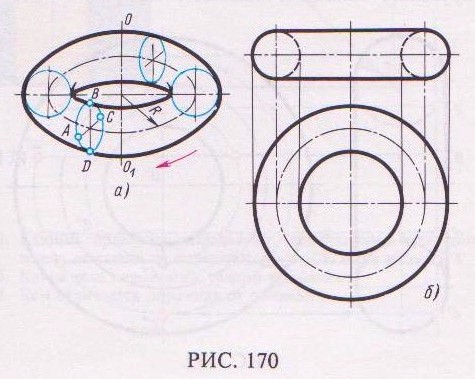
Поверхность кругового кольца (рис. 170, а) образована вращением образующей окружности ABCD вокруг оси ОО1.
Тор – поверхность, образованная вращением части дуги окружности, являющейся образующей, вокруг оси ОО1, расположенной в плоскости этой окружности и не проходящей через ее центр.
На рис. 171, а и б приведены два вида тора. В первом случае образующая дуга окружности радиуса R отстоит от оси вращения на расстоянии меньше радиуса R, а во втором случае – больше.
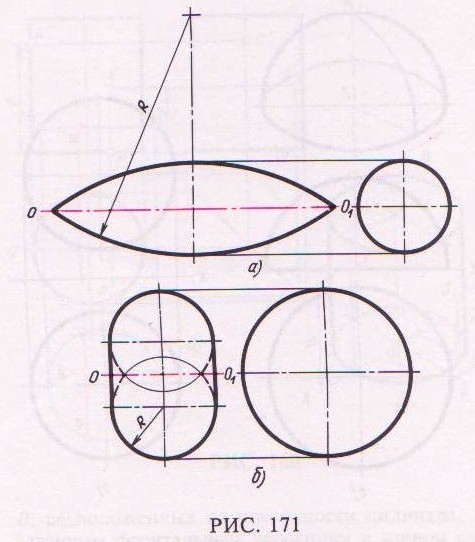
В обоих случаях фронтальные проекции тора представляют собой действительный вид двух образующих дуг окружности радиуса R, расположенных симметрично относительно фронтальной проекции оси вращения. Профильными проекциями тора будут окружности.
Круговое кольцо (или открытый тор) имеет горизонтальную проекцию в виде двух концентрических окружностей, разность радиусов которых равна толщине кольца или диаметру образующей окружности (рис. 170, б). Фронтальная проекция ограничивается справа и слева дугами полуокружностей диаметра образующей окружности.
В случае, когда точка А лежит на поверхности кругового кольца и дана одна ее проекция, для
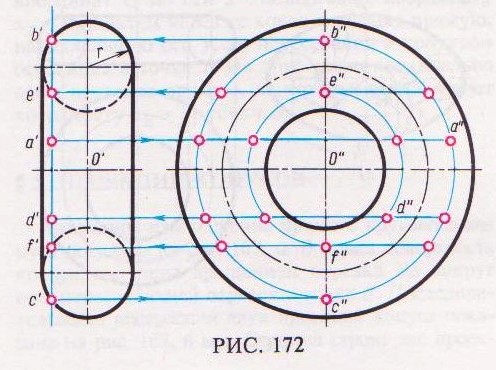
нахождения второй проекции этой точки применяется вспомогательная окружность, проходящая через данную точку А и расположенная на поверхности кольца в плоскости, перпендикулярной оси кольца (рис. 172).
Если задана фронтальная проекция а' точки А. лежащей на поверхности кольца, то для нахождения ее второй проекции (в данном случае – профильной) через а' проводят фронтальную проекцию вспомогательной окружности – отрезок вертикальной прямой линии b'с'. Затем строят профильную проекцию b" с" этой окружности и на ней, применяя линию связи, находят точку а".
Если задана профильная проекция а" точки D. расположенной на поверхности этого кольца, то для нахождения фронтальной проекции точки D через d" проводят профильную проекцию вспомогательной окружности радиуса O" d". Затем через верхнюю и нижнюю точки e" f" этой окружности проводят горизонтальные линии связи до пересечения с фронтальными проекциями образующей окружности радиуса г и получают точки е' и f '. Эти точки соединяют вертикальной прямой, которая представляет собой фронтальную проекцию вспомогательной окружности (она будет невидима). Проводя горизонтальную линию связи из точки d" до пересечения с прямой е' f ', пoлyчaeм искомую точку d'.
Такие же приемы построения применимы и да точек, находящихся на поверхности тора.