Сечение пирамиды плоскостью

Правильная шестиугольная пирамида, пересе­ченная фронтально-проецирующей плоскостью Р, показана на рис. 180.

Как и в предыдущих примерах, фронтальная проекция сечения совпадает с фронтальным сле-

дом P_v плоскости. Горизонтальную и профильную проекции фигуры сечения строят по точкам, кото­рые являются точками пересечения плоскости Р с ребрами пирамиды.

Действительный вид фигуры сечения в этом примере определяется способом совмещения.

Развертка боковой поверхности усеченной пи­рамиды с фигурой сечения и фигурой основания приведена на рис. 180, б.

Сначала строят развертку неусеченной пирами­ды, все грани которой, имеющие форму треуголь­ника, одинаковы. На плоскости намечают точку s_l (вершину пирамиды) и из нее, как из центра, проводят дугу окружности радиусом R, равным действительной длине бокового ребра пирамиды. Действительную длину ребра можно определить по профильной проекции пирамиды, например отрезки s" e" или s" b", так как эти ребра парал­лельны плоскости W и изображаются на ней дей­ствительной длиной. Далее по дуге окружности от любой точки, например а₁, откладывают шесть одинаковых отрезков, равных действительной длине стороны шестиугольника – основания пира­миды. Действительную длину стороны основания пирамиды получаем на горизонтальной проекции (отрезок ab). Точки a ₁... f₁ соединяют прямыми с вершиной s₁. Затем от вершины a₁ на этих пря­мых откладывают действительные длины отрезков ребер до секущей плоскости.

На профильной проекции усеченной пирамиды имеются действительные длины только двух от-

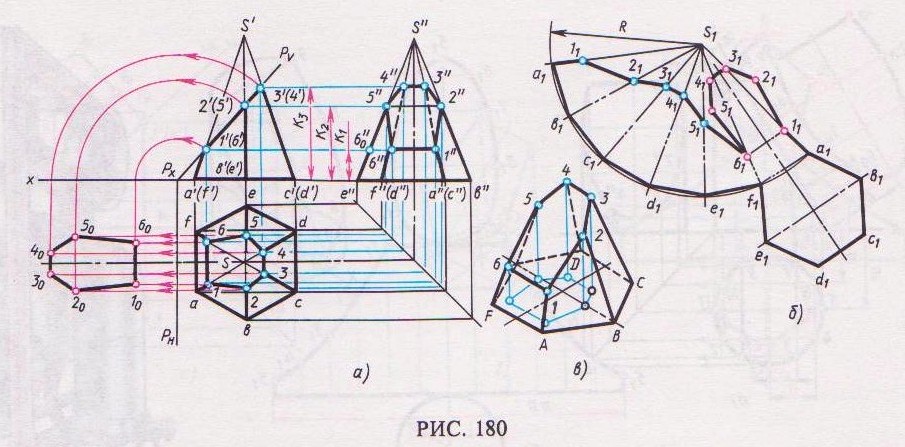
резкое – s" 5 и s" 2. Действительные длины ос­тальных отрезков определяют способом вращения их вокруг оси, перпендикулярной к плоскости Н и проходящей через вершину s. Например, повер­нув отрезок s" 6" около оси до положения, парал­лельного плоскости W, получим на этой плоскости его действительную длину. Для этого достаточно через точку 6" провести горизонтальную прямую до пересечения с действительной длиной ребра SE или SB. Отрезок s" 6₀″ (см. рис. 180).

Полученные точки 1₁ 2₁, 3₁, и т.д. соединяют прямыми и пристраивают фигуры основания и сечения, пользуясь методом триангуляции. Линии сгиба на развертке проводят штрихпунктирной линией с двумя точками.

Построение изометрической проекции усечен­ной пирамиды начинают с построения изометри­ческой проекции основания пирамиды по разме­рам, взятым с горизонтальной проекции комплек­сного чертежа. Затем на плоскости основания по координатам точек 1...6 строят горизонтальную проекцию сечения (см. тонкие синие линии на рис. 180, а, в). Из вершин полученного шести­угольника проводят вертикальные прямые, на которых откладывают координаты, взятые с фрон­тальной или профильной проекций призмы, на­пример, отрезки К_{, К₂, К₃ и т.д. Полученные точки 1...6 соединяем, получаем фигуру сечения. Соединив точки 1...6 с вершинами шестиугольни­ка, основания пирамиды, получим изометричес­кую проекцию усеченной пирамиды. Невидимые ребра изображают штриховыми линиями.

Пример сечения треугольной неправильной пирамиды фронтально-проецирующей плоскостью показан на рис. 181.

Все ребра на трех плоскостях проекций изобра­жены с искажением. Горизонтальная проекция

основания представляет собой его действительный вид, так как основание пирамиды расположено на плоскости Н.

Действительный вид 1 ₀, 2₀, 3 ₀ фигуры сечения получен способом перемены плоскостей проекций. В данном примере горизонтальная плоскость про­екций Н заменена новой плоскостью, которая параллельна плоскости Р; новая ось х₁ совмещена со следом Р_V (рис. 181, а).

Развертку поверхности пирамиды строят следующим образом. Способом вращения находят дей­ствительную длину ребер пирамиды и их отрезков от основания до секущей плоскости Р.

Например, действительные длины ребра SC иего отрезка СЗ равны соответственно длине фрон­тальной проекции s'c' ребра и отрезка c₁′ 3₁ по­сле поворота.

Затем строят развертку треугольной неправильной пирамиды (рис. 181, в). Для этого из произ­вольной точки S проводят прямую, на кот, откладывают действительную длину ребра SA. Из точки s делают засечку радиусом R₁, равным действительной длине ребра SB, а из точки засечку радиусом R₂, равным стороне основания пирамиды АВ, в результате чего получают точку b₁ и грань s₁b₁a₁. Затем из точек s и b₁ как из центров, делают засечки радиусами, равными действительной длине ребра SC и стороне ВС получают грань s₁b₁с₁ пирамиды. Также строится грань s₁с₁a₁.

От точек а₁b₁ и с₁ откладывают действительные длины отрезков ребер, которые берут на фронтальной проекции (отрезки а₁′ 1₁′, b₁′ 2₁′, с₁′ 3₁′). Используя метод триангуляции, пристраивают основание и фигуру сечения.

Для построения изометрической проекции усе­ченной пирамиды (рис. 181, б) проводят изомет­рическую ось х. По координатам т и п строят основание пирамиды ABC. Сторона основания АС параллельна оси х или совпадает с осью х. Как и в предыдущем примере, строят изометрическую проекцию горизонтальной проекции фигуры сече­ния 1₂2₂3₂ (используя точки I, III и IV). Из этих точек проводят вертикальные прямые, на которых откладывают отрезки, взятые с фронтальной или профильной проекции призмы К₁, К₂ и К₃. Полу­ченные точки 1, 2, 3 соединяют прямыми между собой и с вершинами основания.