
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сечение призмы плоскостью
|
|
Фигура сечения прямой пятиугольной призмы фронтально-проецирующей плоскостью Р (рис.178, а) представляет собой плоский пятиугольник 1 2 3 4 5.
Для построения проекций фигуры сечения находят проекции точек пересечения плоскости Р с ребрами призмы и соединяют их прямыми линиями. Фронтальные проекции этих точек получаются при пересечении фронтальных проекций ребер
призмы с фронтальным следом PV секущей плоскости Р (точки 1′...5').
Горизонтальные проекции точек пересечения 1...5 совпадают с горизонтальными проекциями ребер. Имея две проекции этих точек, с помощью линий связи находят профильные проекции 1 ″ ...5", Полученные точки 1″...5" соединяют прямыми линиями и получают профильную проекцию фигуры сечения.
Действительный вид фигуры сечения можно определить любым из способов: вращения, совмещения или перемены плоскостей проекций (см. гл. 15).
В данном примере (рис. 178, а) применен способ перемены плоскостей проекций. Горизонтальная плоскость проекций заменена новой Н1 причем ось х1 (для упрощения построений) совпадает с фронтальным следом плоскости Р.
Для нахождения новой горизонтальной проекции какой-либо точки фигуры сечения (например, точки 1) необходимо выполнить следующие построения. Из точки 1 ' восставляют перпендикуляр к новой оси х1 и откладывают на нем расстояние от прежней оси х до прежней горизонтальной проекции точки 1, т.е. отрезок п. В результате получают точку 1 0. Так же находят и новые горизонтальные проекции точек 2...5. Соединив прямыми линиями новые горизонтальные проекции 1 0... 5 0, получают действительный вид фигуры сечения.
Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).
Развертку боковой поверхности (рис. 178, б) с основанием и фигурой сечения призмы строят следующим образом. Проводят прямую, на которой откладывают пять отрезков, равных длинам сторон пятиугольника, лежащего в основании призмы. Из полученных точек проводят перпендикуляры, на которых откладывают действительные длины ребер усеченной призмы, беря их с фронтальной или профильной проекции (рис. 178, а), получают развертку боковой поверхности призмы.
К развертке боковой поверхности пристраивают фигуру нижнего основания – пятиугольник и фигуру сечения. При этом используют метод триангуляции (см. рис. 50, б) или метод координат, известный из геометрического черчения. На рис. 178, а показано построение вершины 5 методом триангуляции. Линии сгиба по ГОСТ 2.303–68 показывают на развертке штрих-пунктирной линией с двумя точками.
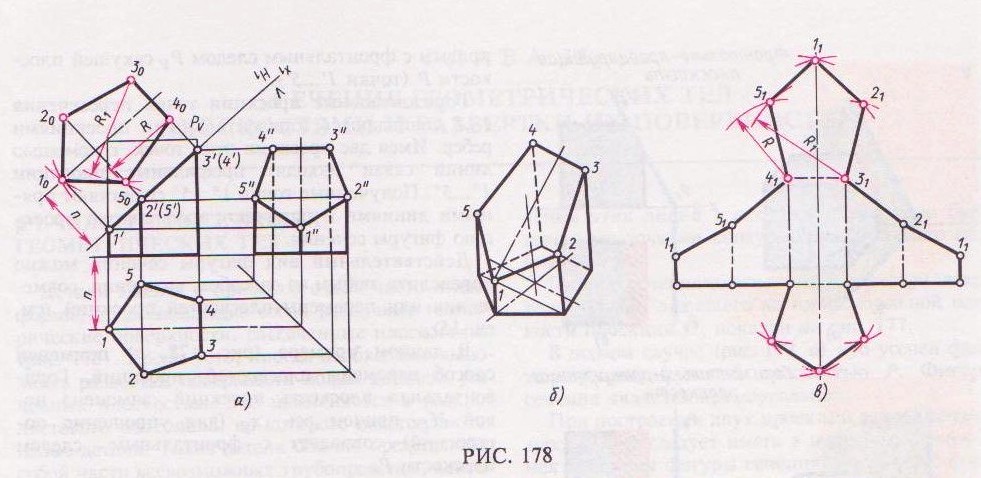
Для наглядности выполним построение усеченного тела в аксонометрической проекции. На рис. 178, в построена изометрическая проекция усеченной призмы. Порядок построения изометрической проекции следующий. Строят изометрическую проекцию основания призмы; проводят в вертикальном направлении линии ребер, на которых от основания откладывают их действительные длины, взятые с фронтальной или профильной проекции призмы. Полученные точки 1'...5' соединяют прямыми линиями.