Сечение прямого кругового конуса плоскостью

В зависимости от расположения секцией плос­кости Р относительно оси прямого кругового кону­са получаются различные фигуры сечения, огра­ниченные кривыми линиями.

Сечение прямого кругового конуса фронтально-проецирующей плоскостью Р рассматривается на рис. 182. Основание конуса расположено на плос­кости Н. Фигура сечения в данном случае будет ограничена эллипсом.

Фронтальная проекция фигуры сечения распо­ложена на фронтальном следе плоскости Р (рис. 182, а).

Для построения горизонтальной проекции кон­тура фигуры сечения горизонтальную проекцию основания конуса (окружности) делят, например, на 12 равных частей. Через точки деления на горизонтальной и фронтальной проекциях прово­дят вспомогательные образующие. Сначала нахо­дят фронтальные проекции точек сечения 1′...12', лежащих на плоскости P₁. Затем с по­мощью линии связи находят их горизонтальные проекции. Например, горизонтальная проекция точки 2, расположенной на образующей s2, прое­цируется на горизонтальную проекцию этой же образующей в точку 2.

Найденные горизонтальные проекции точек контура сечения соединяют по лекалу. Действи­тельный вид фигуры сечения в данном примере найден способом перемены плоскости проекций. Плоскость Я заменяется новой плоскостью проек­ции Н₁.

На фронтальной плоскости проекции V фигура сечения – эллипс изображается в виде прямой 1'7', совпадающей с фронтальной проекцией секущей плоскости Р. Эта прямая 1′ 7' является большой осью эллипса. Малая ось эллипса а'b' перпендикулярна к большой оси 1′ 7' и проходит

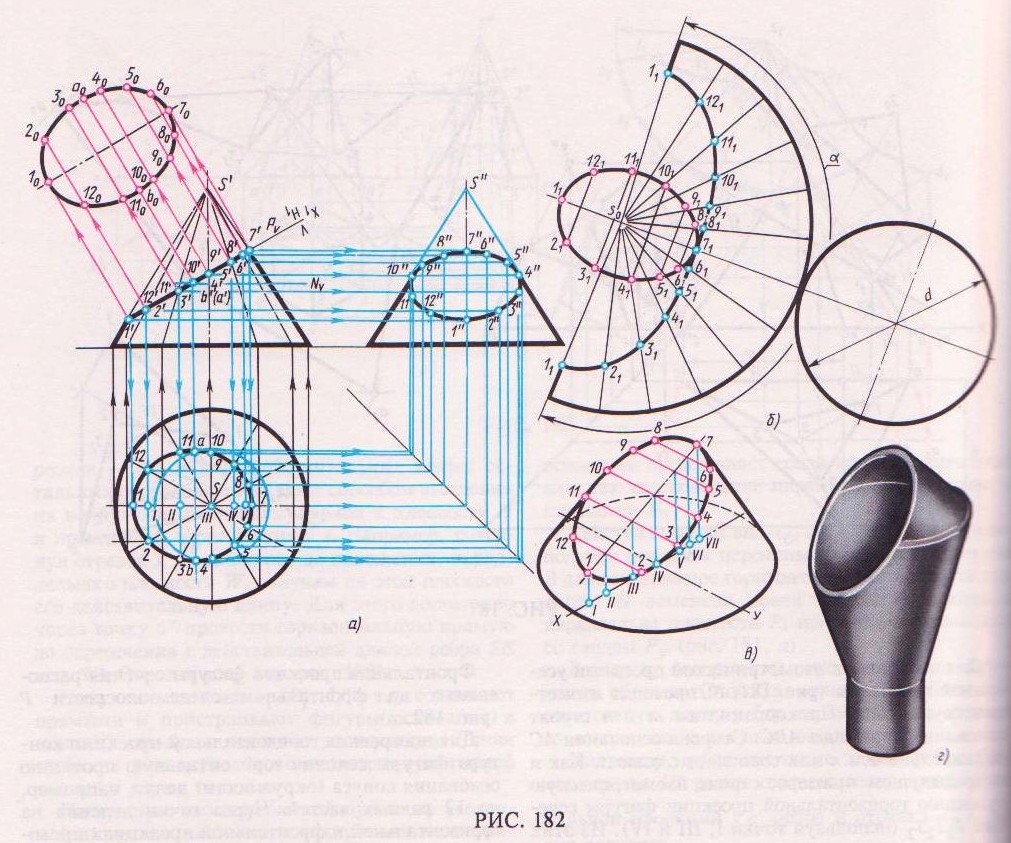
через ее середину. Чтобы найти малую ось сече­ния, через середину большой оси 1′ 7' эллипса проводят горизонтальную плоскость N, которая рассечет конус по окружности, диаметр которой будет равняться малой оси эллипса (a₀b₀).

Построение развертки поверхности конуса (рис. 182, б) начинают с проведения дуги окруж­ности радиусом, равным длине образующей кону­са из точки S₀. Длина дуги определяется углом α:

где d – диаметр окружности основания конуса; l – длина образующей конуса.

Дугу делят на 12 частей и полученные точки соединяют с вершиной s₀. От вершины откладыва­ют действительные длины отрезков образующих от вершины конуса до секущей плоскости Р.

Действительные длины этих отрезков находят,

как и в примере с пирамидой, способом в около вертикальной оси, проводящей через шину конуса. Так, например, чтобы получитьдействительную длину отрезка S2, надо из 2′ провести горизонтальную прямую до пересечения в точке b' с контурной образующей конуса, являющейся действительной ее длиной.

К развертке конической поверхности пристраивают фигуры сечения и основания конуса.

Построение изометрической проекции усеченного конуса (рис. 182, в) начинают с по" основания – эллипса. Изометрическую проекцию любой точки кривой сечения находят с п. трех координат, как показано на рис. 182, в.

На оси х откладывают точки I...VII, взятые с горизонтальной проекции конуса. Из полученных точек проводят вертикальные прямые, на которых откладывают координаты z, взятые с фронтальной проекции. Через полученные на наклонной оси

эллипса точки проводят прямые, параллельные оси у, и на них откладывают отрезки 6₀8₀ и 4₀10₀, взятые на действительном виде сечения.

Найденные точки соединяют по лекалу. Край­ние очерковые образующие проводят по каса­тельной к контуру основания конуса и эллипса.

Пример сечения прямого кругового конуса при­веден на рис. 182, г. Колпак сепаратора представ­ляет собой сварную конструкцию из тонкой лис­товой стали и состоит из двух конусов.