Пересечение прямой линии с поверхностями тел

Конструкции деталей можно рассматривать как сочетание различных геометрических тел. Необхо­димо уметь строить линии пересечения поверхнос­тей этих тел. Пример, где требуется подобное по­строение, показан на рис. 195, на котором изо­бражен бункер, ограниченный цилиндрической поверхностью А, пересекающейся с конической поверхностью Б и поверхностью пирамиды В.

В зависимости от вида поверхностей тел линии пересечения могут быть лекальными кривыми или ломаными.

Для решения задач на построение линий пере­сечения поверхностей необходимо предварительно усвоить построение точек пересечения прямой с поверхностями различных геометрических тел.

Если прямая пересекается с поверхностью тела, получаются две точки, одновременно принадлежа­щие как поверхности тела, так и прямой линии.

Такие точки называются точками входа и выхода (рис. 196, а; точки N и М). Для нахождения этих точек выполняются построения в следующем по­рядке.

Через данную прямую проводят вспомогатель­ную плоскость (обычно проецирующую). Напри­мер, на рис. 196, а, где изображено пересечение прямой АВ с поверхностью пирамиды, через пря­мую проведена вспомогательная горизонтально-проецирующая плоскость Р. Затем находят линии пересечения вспомогательной плоскости с повер­хностью данного геометрического тела (линии КС и ED). На пересечении полученных линий с за­данной прямой находят искомые точки (точки N и М).

На комплексном чертеже точки входа и выход определяют следующим образом (рис. 196, б). Горизонтальные проекции кс и ed прямых КС к ED совпадают с горизонтальным следом плоскости Р_Н. Фронтальные проекции точек к', с', е' и d′ определяют, пользуясь вертикальными линиями

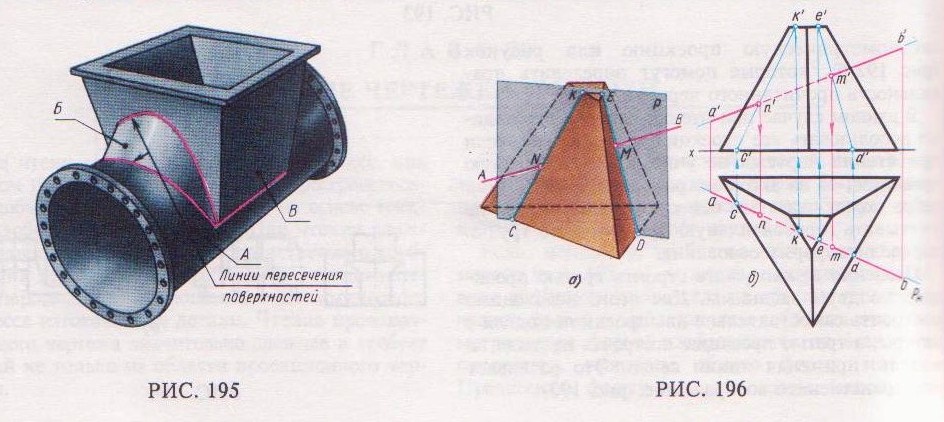
связи, проведенными из точек к, с, е и d до пере­сечения с фронтальными проекциями основания пирамиды. Соединяют точки к' с с' и е' с d' прямыми. На пересечении фронтальных проекций найденных прямых с проекцией а'b' данной пря­мой получают фронтальные проекции п' и т' искомых точек входа и выхода. Проведя через них вертикальные линии связи, находят горизонталь­ные проекции п и т этих точек.

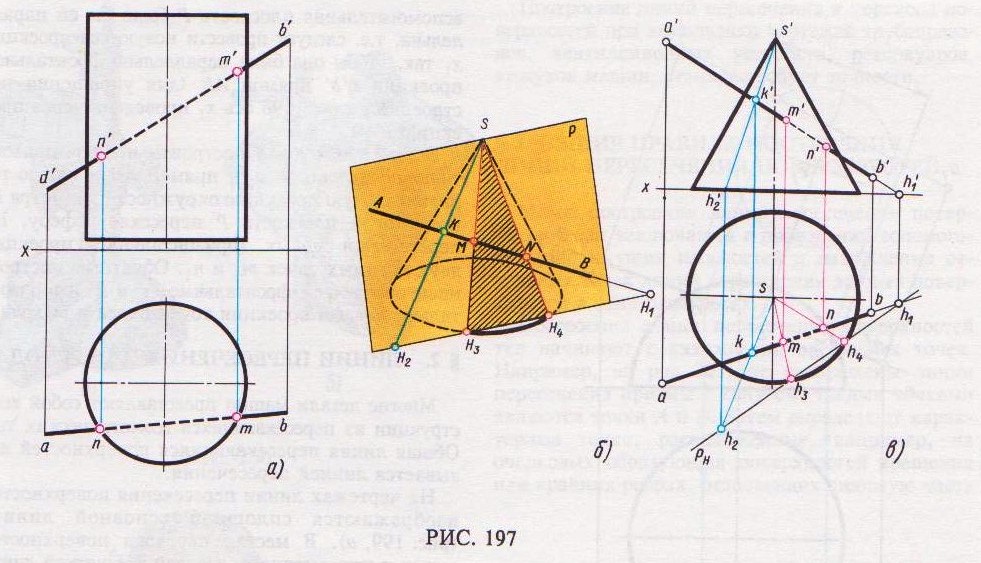
В некоторых частных случаях можно обой­тись без применения вспомогательной плоскос­ти. Например, точки входа и выхода прямой АВ с поверхностью прямого кругового цилин­дра (рис. 197, а) определяют следующим образом.

Горизонтальная проекция цилиндрической по­верхности представляет собой окружность, поэто­му горизонтальные проекции всех точек, располо­женных на цилиндрической поверхности, в том числе и двух искомых точек, будут расположены на этой окружности (рис. 197, а).

Фронтальные проекции п' и m' искомых точек определяют, проводя через точки п и т верти­кальные линии связи до встречи с данной фрон­тальной проекцией а'b' прямой АВ.

На рис. 197, б, в показано построение точек входа и выхода прямой АВ и поверхности прямого кругового конуса. Через прямую АВ проводят вспомогательную плоскость Р, проходящую через вершину конуса. Плоскость Р пересечет конус по образующим SН₃ SН₄.

На комплексном чертеже изображение плос­кости Р строят следующим образом. На прямой АВ берут произвольную точку К и соединяют ее с вершиной S конуса прямой линией. Две пересе­кающиеся прямые АВ и SK определяют плоскость Р.

Чтобы найти точки входа и выхода, необходимо построить горизонтальные проекции образующих SHз и SH₄. Для этого продолжим s'k' и а'b' до

пересечения с осью х в точках h₂′ и h₁ ′. Опустим линию связи из точки к' до пересечения с аb, полученную точку к соединим с s. Продлим гори­зонтальную проекцию прямой SK до пересечения с линией связи, опущенной из точки h₂′, получим точку h ₂. Из точки h₁′, проведем линию связи до пересечения с продолжением прямой ab, получим точку h₁. Через следы h₁ и h ₂ пройдет горизон­тальный след плоскости Р. Точки h₁ и h ₂ соеди­ним прямой и получим горизонтальный след Р_H плоскости Р.

Основание конуса является горизонтальным следом конической поверхности. Поэтому, опреде­лив точки пересечения этого следа со следом Р_H плоскости Р, можно найти и те две образующие, по которым коническая поверхность пересекается вспомогательной плоскостью Р. На комплексном чертеже горизонтальная проекция основания ко­нуса (окружность) пересекается со следом Р_H в точках h ₃ и h ₄. Эти точки соединяют с вершиной

s и получают следы sh₃ и sh₄ образующих SН₃ и SH₄.

На пересечении найденных образующих с дан­ной прямой АВ находят искомые точки М и N – точки входа и выхода прямой АВ с конической поверхностью.

Горизонтальные проекции точек т и п находят на пересечении горизонтальных проекций обра­зующих sh ₃ и sh ₄ с горизонтальной проекцией прямой ab. Через точки т и п проводят верти­кальные линии связи до пересечения а'b' инахо­дят фронтальные проекции т' и п' точек входа и выхода.

Точки входа и выхода прямой АВ с повер­хностью сферы (рис. 198) находят, проведя через прямую АВ вспомогательную фронтально-проеци­рующую плоскость Р.

Вспомогательная плоскость Р пересекает сферу по окружности, которая проецируется на плос­кость Н в виде эллипса, что затрудняет построе­ние. Поэтому в данном случае необходимо приме­нить способ перемены плоскостей проекций. Но­вую плоскость проекций выбирают так, чтобы

вспомогательная плоскость Р была бы ей парал­лельна, т.е. следует провести новую ось проекций x₁ так, чтобы она была параллельна фронтальной проекции а'b' прямой АВ (для упрощения по­строений на рис. 198 ось х₁ проведена через про­екцию а'b').

Затем необходимо построить новую горизон­тальную проекцию a₁b₁ прямой АВ иновую го­ризонтальную проекцию окружности диаметра D. по которой плоскость Р пересекает сферу. На пересечении новых горизонтальных проекций двух искомых точек т₁ и n₁. Обратным построе­нием определяем фронтальные т' и п' и горизон­тальные т и п проекции точек входа и выхода.