Упражнение 18.8. Решение дифференциальных уравнений

Задача. Найти функцию у(х), удовлетворяющую дифференциальному уравнению

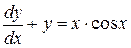и имеющую значение 0 при х = 0.

Анализ. Это простое дифференциальное уравнение допускает точное аналитическое решение, однако в данном упражнении предполагается использование стандартной функции программы MathCad, осуществляющей численное решение данного уравнения. Результат вычислений можно после этого сравнить с точным решением.

1. Запустите программу MathCad.

2. Задайте начальное значение функции как элемент вектора у, размерность которого соответствует числу решаемых уравнений (в данном случае единице): у₀: = 0.

3. Создайте функцию Т(х, у}, которая вычисляет значение производной при заданных значениях независимой переменной и неизвестной функции:

Т(х, у): = - y₀ + x× cos(x).

4. Определите начальное (точка 0) и конечное значение отрезка интегрирования.

а: = 0, b: = 12 × p.

5. Укажите число шагов интегрирования.

К: = 20.

6. Вычислите численное решение уравнения при помощи функции rkfixed.

Z: = rkfixed (y, a, b, K, T).

Рис. 18.7. Графики численного и точного решения дифференциального уравнения

Результат вычислений — матрица Z с двумя столбцами, первый из которых содержит значения независимой переменной, а второй — соответствующие значения функции.

7.Постройте график полученного решения.

8.Определите аналитическое решение данного уравнения при тех же начальных условиях.

9.Нанесите аналитическую кривую на тот же график и сравните поведение численного и точного решения.

10. Измените число шагов, на которые делится отрезок интегрирования, и исследуйте, как изменяется результат расчета при уменьшении и увеличении этого параметра.

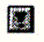Мы научились численно решать дифференциальные уравнения первого порядка с помощью программы MathCad. Использованный метод без изменений переносится на системы, содержащие два или большее число дифференциальных уравнений. Увеличение величины шага интегрирования ускоряет получение результата, но снижает его точность. При слишком большой величине шага результат расчетов может вообще не соответствовать реальному решению.