
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример расчета опор
|
|
Проверить прочность и устойчивость корпуса цилиндрического аппарата с эллиптическими днищами, лежащего на трех опорах (рис. 1.19, схема II), от действия силы тяжести по следующим данным. Корпус аппарата DH = 2, 02 м; DB = 2, 0 м; S - C = 8 мм; С= 2 мм; Lц =10, 9 м. Днище:
DB = 2, 0 м; h= 0, 55 м; Gдн = 0, 0036 МН; Vдн = 1, 17 м3.
Материал корпуса и днища - сталь (Е = 2, 05 × 105 МН/м2;
[ s ] = 240 МН/м2; [ s ]u = 146 МН/м2; r =7, 85 × 103 кг/м3).
Среда r c = 1000 кг/м3; давление Р= 1, 0 МН/м2.
Сила тяжести заполненного водой аппарата при гидроиспытании Gmax = 0, 35 МН.
Расчет производим для средней опоры, имеющей наибольшую нагрузку. Реакцию опоры определяем по формуле (1.48).
РБ = 0, 354 × Gmax = 0, 354 × 0, 35 = 0, 124 МН.
Приведенную длину днища определяем по формуле (1.52):
Lдн 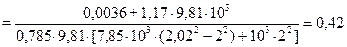 м.
м.
Приведенную длину аппарата определяем по формуле (1.50):
Lпр = 10, 9 + 2 × 0, 42 = 11, 74 м.
Расстояние между опорами при l1 = 0, 145 × Lпр (см. рис.19).
l = 0, 5 × (Lпр -2× l1) = 0, 5 × (11, 74 -2 × 0, 145 × 11, 74) = 4, 16 м.
Расчетный изгибающий момент от силы тяжести определяется по формуле (1.50):
Mи =0, 0105 × 0, 35 × 11, 74 = 0, 0432 МН × м.
Напряжение на изгиб в корпусе от силы тяжести определяем по формулам (1.52) и (1.53).
Gи = 0, 0432 / 0, 8 × 22 × 0, 008 = 1, 69 МН/м2,
т.е. напряжения ничтожно малы. Поэтому на устойчивость корпус не проверяем.
Выбираем ширину опоры по рис. 1.14:
в = 0, 2 × DB = 0, 2 × 2, 0 = 0, 4 м.
Момент сопротивления расчетного сечения стенки корпуса над опорой определяем по формуле (1.60):
W’ = 0, 4 + 8 × 0, 008 × 0, 0082 / 6 = 4, 95 × 10-6 м3.
Напряжение на изгиб в стенке аппарата от действия реакции опоры определяем по формуле (1.59):
s u =(0, 02 × 0, 124 × 2, 02) / 4, 95 × 10-6 = 1010 МН/м2
т.е. s u > [ s ]u = 146 МН/м2, следовательно, требуется усилить стенку над опорой накладкой.
Требуемый момент сопротивления усиленного сечения элемента стенки определяем по формуле (1.61):
W ³ (0, 02 × 0, 124 × 2, 02) / 146 = 34, 3 × 10-6 м3.
Поскольку 4 × [ s ]u = 4 × 146 = 584 МН/м2 < s u = 1010 МН/м2, принимаем толщину накладки SH = 1, 6 × 10 = 16 мм.
Расчетную площадь поперечного сечения стенки корпуса определяем по формуле (1.62)
Fс’ = 0, 4 + 8 × 0, 008 × 0, 008 = 37 × 10-4 м2.
Расчетную площадь поперечного сечения накладки определяем по формуле (1.63):
Fн’= (0, 4 + 4 × 0, 016) × 0, 016 = 74 × 10-4 м2.
Момент инерции площади Fс’ определяем по формуле (1.64):
Iс = (37 × 10-4 × 0, 0082) / 12 = 1, 97 × 10-8 м4.
Момент инерции площади Fн’ определяем по формуле (1.64):
Iн = (74 × 10-4 × 0, 0162) / 12 = 15, 8 × 10-8 м4.
Расстояние от нижней поверхности накладки до центра тяжести площади определяем по формуле (1.65):
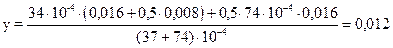 м
м
Расчетный момент сопротивления, усиленного накладкой сечения корпуса определяем по формуле (1.62):
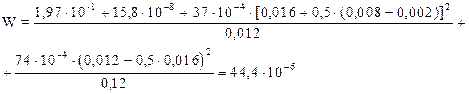
т.е. W > 34, 3 × 10-6 м3 - значения, определенного выше по формуле (1.60), т.е. прочность обеспечена.