
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модель “затраты- выпуск” (модель В. Леонтьева).
|
|
24. Модель В.Леонтьева, называемая также линейной балансовой моделью, является одним из основных приближений при моделировании систем, состоящих из нескольких взаимосвязанных процессов. Основные типы модели:
1. Открытая модель - моделируемый объект не самодостаточен, есть взаимодействующая с ним окружающая социально-экономическая среда, модель не учитывает воспроизводство трудового ресурса - нет модели домашних хозяйств.
2. Закрытая модель - моделируется замкнутая социально-экономическая система, влияние внешних факторов на которую пренебрежимо мало, учитывается воспроизводство в домашних хозяйствах.
3. Статическая модель - все коэффициенты модели не зависят от времени, постоянны интенсивности экономических процессов, протекающих в системе, весь объём производства расходуется только на потребление и его достаточно для воспроизводства трудового ресурса на постоянном уровне.
4. Динамическая модель - все коэффициенты модели не зависят от времени, есть зависимость интенсивностей экономических процессов, протекающих в системе, от времени. Либо не весь объём производства расходуется на потребление и его достаточно для расширения производства тех видов продукции, на которые имеется растущий спрос, либо объём производства недостаточен для воспроизводства трудового ресурса на постоянном уровне.
Это даёт 4 основных варианта балансовой модели.
| Типы модели | Открытая | Закрытая |
| Статическая | Открытая статическая модель Леонтьева | Закрытая статическая модель Леонтьева |
| Динамическая | Открытая динамическая модель Леонтьева | Закрытая динамическая модель Леонтьева |
25. Простейшей формой модели является открытая статическая линейная балансовая модель. Сформулируем для начала условия и варианты применения, а так же основные приближения, используемые при её построении.
Первое условие применения открытой линейной балансовой модели - моделируемый экономический объект состоит из нескольких (n штук) взаимосвязанных процессов (отраслей), то- есть имеет структуру. В каждом из процессов (с номером i) получается некоторый продукт (полный объём продукта - xi), часть которого расходуется в этом же и некоторых других процессах. Оставшиеся после этого объёмы продуктов (конечмные объёмы продуктов или объёмы конечного потребления yi) являются конечными, выходными результатами для всей модели. Свойство наличия баланса состоит как раз в том, что полные объёмы всей продукции складываются только из объёмов её конечного потребления и объёмов потребления продукции в производственных процессах (межотраслевых потоков). Примером такой взаимосвязи может служить, например, потребление с/х продукции машиностроением, добывающей, лёгкой и пищевой промышленностью, и наоборот, потребление продукции машиностроения и добывающей промышленности сельским хозяйством. При этом у этих отраслей имеются значительные сторонние заказы, т.е. объёмы конечного потребления.
Второе условие - свойство открытости состоит в том, что в этой модели не делается попыток задать структуру объёма конечного потребления, требуется просто найти его.
Третье условие - количество каждого продукта (с номером j), расходуемого при получении единицы результирующего продукта номер i, не зависит от конкретных объёмов произведённых продуктов (нет оптовых скидок) и является постоянной величиной aji. Все эти величины образуют квадратную (n´ n) матрицу технологических, или структурных коэффициентов (коэффициентов прямых материальных затрат) А =(aji) n´ n. величина трудозатрат на единицу i -й продукции также является постоянной величиной K i и измеряется в человекочасах. - стоимость человекочаса - одинакова для всех отраслей.
Варианты применения открытой модели Леонтьева: моделирование экономической деятельности всего мирового сообщества, отдельно взятого государства, отдельной отрасли или фирмы. Возможны две формы этой модели: баланс за весь рассматриваемый период и моментальный баланс, в котором участвуют не объёмы, а интенсивности производства и потребления.
Приближения:
1) в случае моментального баланса все интенсивности не зависят от времени, при расчёте баланса за весь период они могут произвольно меняться, но информация об этом теряется.
2) Все коэффициенты модели (aji, K i, ) от времени не зависят (она статическая).
3) Модель линейная (см. выше).
27. Решим в этой модели прямую задачу, то есть попытаемся найти уравнения баланса – выражения для вычисления объёмов конечного потребления, полный объём трудозатрат и цены на продукцию. Для этого рассмотрим, что происходит с полным объёмом j -й продукции xj. Он расходуется на производство продукции других видов (в том числе и на воспроизводство j -й продукции) а также на конечное потребление (т.е. собственно потребление и накопление). Так как, согласно свойству линейности, количество j- го продукта, расходуемого при получении единицы i- го продукта является постоянной величиной aji, то для производства всего объёма i- го продукта потребуется aji × xi, а для производства всех видов продукции - 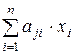 единиц j -й продукции. Вместе с конечным потреблением это даёт полный объём xj:
единиц j -й продукции. Вместе с конечным потреблением это даёт полный объём xj: 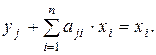 При изменении j от 1 до n это выражение даёт первую группу из n уравнений баланса. Ещё одно выражение получается для полного объёма трудозатрат z при суммировании полных объёмов трудозатрат на каждый вид продукции (произведений K i × xi) по всем видам продукции:
При изменении j от 1 до n это выражение даёт первую группу из n уравнений баланса. Ещё одно выражение получается для полного объёма трудозатрат z при суммировании полных объёмов трудозатрат на каждый вид продукции (произведений K i × xi) по всем видам продукции: 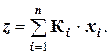 Третья группа из n балансовых уравнений – уравнения для цен на единицу продукта – получается на базе трудовой теории стоимости. Цена единицы j -й продукции P j складывается из издержек производства (цены ресурсов – i -ых продуктов, израсходованных на производство - aij P i) и прибавленной стоимости К j:
Третья группа из n балансовых уравнений – уравнения для цен на единицу продукта – получается на базе трудовой теории стоимости. Цена единицы j -й продукции P j складывается из издержек производства (цены ресурсов – i -ых продуктов, израсходованных на производство - aij P i) и прибавленной стоимости К j: 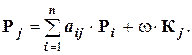 26. Приведём полученную выше полную систему из 2 n +1 уравнений баланса в натуральном выражении:
26. Приведём полученную выше полную систему из 2 n +1 уравнений баланса в натуральном выражении:
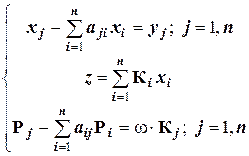 . (1)
. (1)
Введя n- мерные вектора конечного потребления 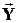 , объёма произведённых продуктов
, объёма произведённых продуктов 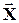 , цен
, цен 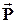 и трудозатрат
и трудозатрат 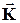 , и используя операцию транспонирования
, и используя операцию транспонирования 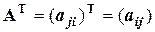 , можно получить матричную форму системы уравнений (1):
, можно получить матричную форму системы уравнений (1):
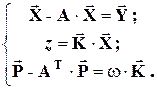 (2)
(2)
Уравнения баланса в форме (1), (2) позволяют по известным полным объёмам продукции и ценам на неё определить объёмы конечного потребления, величины трудозатрат на единицу продукции и полный объём трудозатрат, связанный с количеством занятых в производстве. Если последний действительно является величиной, искомой в процессе анализа экономической системы, то первые два (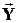 ,
, 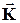 ) являются как раз отправной точкой этого анализа. 28. С точки зрения анализа поведения экономической системы важной является задача, обратная к решённой выше, т.е. задача определения полных объёмов продукции, цен на неё и числа занятых в производстве по известным технологическим и демографическим характеристикам системы, прямо связанным с объёмами конечного потребления и величинами трудозатрат на единицу продукции, то есть определение
) являются как раз отправной точкой этого анализа. 28. С точки зрения анализа поведения экономической системы важной является задача, обратная к решённой выше, т.е. задача определения полных объёмов продукции, цен на неё и числа занятых в производстве по известным технологическим и демографическим характеристикам системы, прямо связанным с объёмами конечного потребления и величинами трудозатрат на единицу продукции, то есть определение 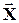 , z и
, z и 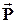 через
через 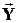 и
и 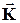 . В силу того, что уравнения (2) являются матричной формой системы линейных уравнений с постоянными коэффициентами по отношению к переменным
. В силу того, что уравнения (2) являются матричной формой системы линейных уравнений с постоянными коэффициентами по отношению к переменным 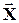 и
и 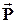 , они могут быть решены с использованием стандартного аппарата линейной алгебры. При этом далее здесь значки векторов у векторных переменных будут опущены, так как любой n - мерный вектор может быть представлен, как матрица – столбец размера (n ´ 1). Решая уравнения (2) и используя соотношение
, они могут быть решены с использованием стандартного аппарата линейной алгебры. При этом далее здесь значки векторов у векторных переменных будут опущены, так как любой n - мерный вектор может быть представлен, как матрица – столбец размера (n ´ 1). Решая уравнения (2) и используя соотношение 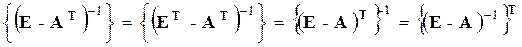 , получим:
, получим:
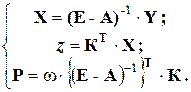 (3)
(3)
Здесь Е=(d ij) n´ n – единичная матрица, а обратная матрица (Е-А)- 1 (её ещё иногда называют матрицей полных затрат) и транспонированная к ней являются неизменными при любых изменениях демографической ситуации (вектор Y) и вычисляются по общему правилу: 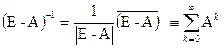 , где | Е-А | - определитель, а
, где | Е-А | - определитель, а 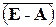 - присоединённая к (Е-А). Приведённое здесь выражение обратной матрицы через ряд является альтернативным способом её вычисления, позволяющим организовать процесс приближённого вычисления (Е-А)- 1 с помощью быстро сходящегося ряда. Это выражение отражает процесс установления равновесия в рассматриваемой экономической системе. матрицы (Е-А)- 1 и {(Е-А)- 1 } Т могут измениться только в случае изменения структуры производства (матрицы А), т.е. технологической революции. Более того, структура цен, как следует из третьего уравнения (3), также может измениться только в случае изменения технологии производства, принятой в обществе, т.е. изменения А и К. Изменение же величины почасовой оплаты , принятой во всём экономическом объекте, приведёт лишь к пропорциональному изменению всех цен, без изменения соотношения между ними. Отдельно замечу, что матрица (Е-А)- 1 обязательно существует, и получаемый из (3) Х имеет экономический смысл (его компоненты положительны) в случае, когда все элементы А неотрицательны и суммы их по столбцам не больше 1, причём хотя бы одна строго меньше. Таким образом, для гарантии получения Х из (3), вообще говоря, может быть необходим подбор специальной системы единиц измерения объёмов Х и Y, в которой матрица А удовлетворяет упомянутым условиям. В принципе, матрица А называется продуктивной, если для любого Y > 0 существует неотрицательное решение Х > 0 любого из уравнений (3).
- присоединённая к (Е-А). Приведённое здесь выражение обратной матрицы через ряд является альтернативным способом её вычисления, позволяющим организовать процесс приближённого вычисления (Е-А)- 1 с помощью быстро сходящегося ряда. Это выражение отражает процесс установления равновесия в рассматриваемой экономической системе. матрицы (Е-А)- 1 и {(Е-А)- 1 } Т могут измениться только в случае изменения структуры производства (матрицы А), т.е. технологической революции. Более того, структура цен, как следует из третьего уравнения (3), также может измениться только в случае изменения технологии производства, принятой в обществе, т.е. изменения А и К. Изменение же величины почасовой оплаты , принятой во всём экономическом объекте, приведёт лишь к пропорциональному изменению всех цен, без изменения соотношения между ними. Отдельно замечу, что матрица (Е-А)- 1 обязательно существует, и получаемый из (3) Х имеет экономический смысл (его компоненты положительны) в случае, когда все элементы А неотрицательны и суммы их по столбцам не больше 1, причём хотя бы одна строго меньше. Таким образом, для гарантии получения Х из (3), вообще говоря, может быть необходим подбор специальной системы единиц измерения объёмов Х и Y, в которой матрица А удовлетворяет упомянутым условиям. В принципе, матрица А называется продуктивной, если для любого Y > 0 существует неотрицательное решение Х > 0 любого из уравнений (3).
29. Существует несколько критериев продуктивности структурной матрицы. Приведем некоторые из них.
Первый критерий продуктивности. Если для матрицы А с неотрицательными элементами и некоторого вектора Y с неотрицательными компонентами уравнение (3) имеет решение Х с неотрицательными компонентами, то матрица А продуктивна.
Иными словами, достаточно установить наличие положительного решения системы (3) хотя бы для одного положительного вектора, чтобы матрица А была продуктивной.
Второй критерий продуктивности. Матрица А с неотрицательными элементами продуктивна тогда и только тогда, когда матрица (E-A)-1 существует и неотрицательна.
Третий критерий продуктивности. Матрица А с неотрицательными элементами продуктивна, если сумма элементов по любому ее столбцу (строке) не превосходит единицы, причем хотя бы для одного столбца (строки) эта сумма строго меньше единицы.
|