
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Поверхности
|
|
С житейской точки зрения поверхность — внешняя сторона предметов. Так утверждают толковые словари. Евклид: “Поверхность есть то, что имеет только длину и ширину”.
В технической практике принято рассматривать образование поверхности (как и линии) с позиций кинематики — движения.
ПОВЕРХНОСТЬ — это множество последовательных положений движущейся линии — образующей.
Образующая может сохранять свою форму или изменять ее — деформироваться. Закон перемещения образующей определяется направляющими линиями, по которым скользит образующая и характером движения образующей. Например, поверхности Каталана (названы так по имени бельгийского ученого, их исследовавшего), или — поверхности с плоскостью параллелизма. Прямолинейная образующая “a” перемещается — скользит по двум направляющим — “n” и “m”, оставаясь параллельной плоскости параллелизма a.
Для изображения поверхности на чертеже, используют КАРКАС — множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае хотя бы одна линия каркаса. Проекции каркаса можно построить, если известен определитель поверхности.
ОПРЕДЕЛИТЕЛЬ ПОВЕРХНОСТИ — совокупность независимых условий, однозначно задающих поверхность.
Различают две части определителя:
— геометрическая часть указывает на геометрические фигуры (точки, линии, поверхности), с помощью которых образовывается поверхность; обозначается (Г);
— алгоритмическая (описательная) часть содержит указания о характере изменения образующей и законе ее перемещения; обозначается [ A ].
Таким образом, определитель пишется в следующей форме:
F(Г)[ A ]
Определитель находят, исходя из кинематического способа образования поверхности. Например, для поверхностей Каталана:
F(m, n)[ a || a]
Для задания этих поверхностей на эпюре Монжа достаточно указать проекции направляющих m и n и положение плоскости параллелизма a (рис. 112).
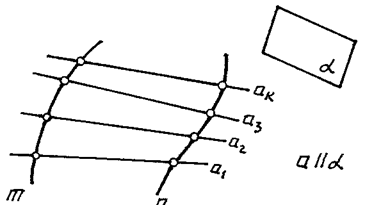
Рис. 112
В геометрическую часть определителя не записывают образующую a. Поверхность линейчатая (образующая — прямая линия). Поэтому априорно известно, что а — прямая.
В алгоритмической части содержится указание, что поверхность Каталана является поверхностью с плоскостью параллелизма. Поэтому в геометрическую часть определителя не записывают также и плоскость параллелизма.