
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ВВЕДЕНИЕ. Линейное программирование (ЛП).
|
|
МЕТОДЫ ОПТИМИЗАЦИИ.
Линейное программирование (ЛП).
Симплекс – метод решения задач ЛП.
Учебное пособие по дисциплине
«Основы САПР»
Тольятти 2003
УДК 002
Методы оптимизации. Линейное программирование (ЛП). Симплекс метод решения задач ЛП: Учебное пособие по дисциплине «Основы САПР»/ сост. Пиастро Г.П., Атлягузова Е.И., Коротыч В.И. - Тольятти: ТГУ, 2003.
Рассматривается математическая модель задачи линейного программирования, в том числе различные формы ее представления. Приводится графическая интерпретация задачи линейного программирования на плоскости и графический способ решения. Выполнен интуитивно - понятный анализ процедуры аналитического решения задачи линейного программирования. Излагается прямой алгоритм симплекс-метода и его графическая иллюстрация, а также прямой алгоритм с искусственными переменными.
Составители: Пиастро Г.П., Атлягузова Е.И., Коротыч В.И.
Научный редактор: Ройтбург Ю.С.
(с) Тольяттинский Государственный Университет, 2003
ОГЛАВЛЕНИЕ.
ВВЕДЕНИЕ.......................................................................................................................................................................................... 3
1. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧИ. АНАЛИЗ ВАРИАНТОВ РЕШЕНИЙ.......................... 4
2. КАНОНИЧЕСКАЯ ФОРМА ПРЕДСТАВЛЕНИЯ ОГРАНИЧЕНИЙ. ДОПУСТИМЫЕ БАЗИСНЫЕ РЕШЕНИЯ. 8
3.СИМПЛЕКС-МЕТОД. АНАЛИЗ ПРОЦЕДУРЫ РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (С ПРИМЕРОМ)..................................................................................................................................................................................... 10
4. ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ.......................................................................................................... 13
5. Прямой алгоритм симплексного метода.................................................................................................. 19
6. Прямой алгоритм с искусственными переменными..................................................................... 26
ВВЕДЕНИЕ.
Задача повышения эффективности технологических и организационных систем (например: металлорежущего станка, автоматической линии, производства в целом) путём принятия обоснованных решений актуальна во всех областях деятельности человека. Количественная оценка эффективности может быть получена при заданной цели функционирования системы, с учётом ограничений на ресурсы, привлекаемые для достижения цели. При этом задача принятия решения ставится как задача выбора параметров системы, обеспечивающих максимизацию или минимизацию целевой функции. Последняя количественно определяет степень достижения цели – величину критерия оптимизации. В качестве критерия можно принять, например, себестоимость изделия (цель-минимизация), быстродействие машины или прибора (цель-максимизация) и другие показатели.
Обоснованное применение количественных методов для принятия решений - оптимизацию поведения структур систем называют исследованием операций (ИСО). Здесь операция – комплекс целенаправленных действий.
Задача, рассмотренная выше, решается с применением математической модели системы, объединяющей упомянутые ограничения на ресурсы и целевую функцию. Нахождение величин упомянутых параметров системы (они входят в математическую модель как неизвестные) путём решения математической задачи называют математическим программированием. Математическое программирование – важнейшая область математики, ориентированная на широкое применение компьютеров. Одним из разделов этой области является линейное программирование.
В моделях линейного программирования так называемая «основная задача» состоит в нахождении неотрицательного решения системы линейных уравнений или неравенств (ограничений), которая минимизирует или максимизирует линейную форму (целевую функцию). Математическая задача линейного программирования записывается в сокращённом виде следующим образом:
найти 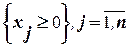
при ограничениях типа:
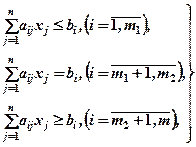 (0.1)
(0.1)
которые минимизируют (или максимизируют) линейную форму – целевую функцию:
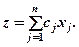 (0.2)
(0.2)
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧИ. АНАЛИЗ ВАРИАНТОВ РЕШЕНИЙ.
Задача линейного программирования геометрически может быть проиллюстрирована следующим образом.
Пусть необходимо найти минимум целевой функции:
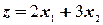 (1.1)
(1.1)
При ограничениях:
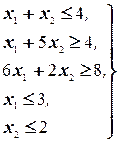 (1.2)
(1.2)
Переменные x1 и x2 должны быть неотрицательными.
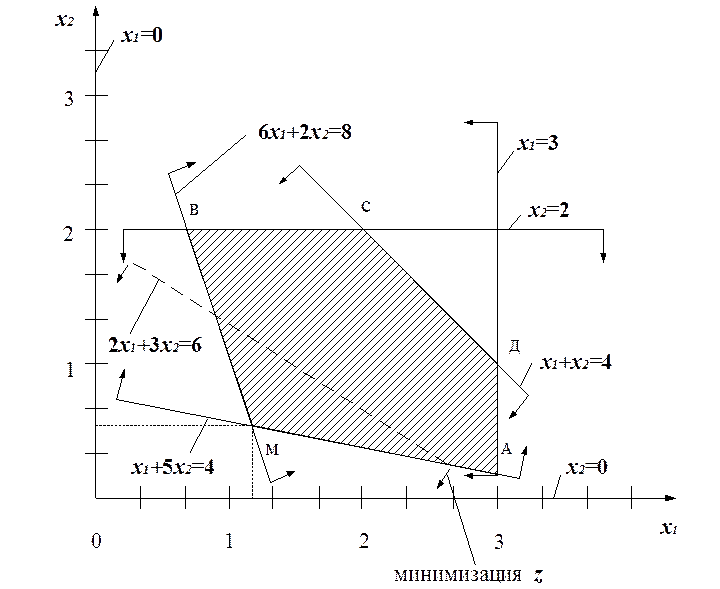
Поэтому множество точек, являющихся возможными (допустимыми) решениями, может находиться в первом квадранте (см. рис. 1.1.). Неравенства–ограничения изображены в виде полуплоскостей, границами которых являются прямые (графики функций), полученные из неравенств путём отбрасывания знаков >, <. Полуплоскости образуют выпуклый многоугольник (многоугольник решений – симплекс).
Линейная форма (линия уровня) 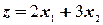 для некоторого набора фиксированных значений переменной z представляет собой семейство параллельных прямых. Одна из них, которая пройдёт через вершину многоугольника «М», ближайшую к началу координат и даст минимум z (для координат вершины).
для некоторого набора фиксированных значений переменной z представляет собой семейство параллельных прямых. Одна из них, которая пройдёт через вершину многоугольника «М», ближайшую к началу координат и даст минимум z (для координат вершины).
Определив координаты точки М (8/7; 4/7) получим:
z = 2× 8/7 + 3× 4/7 = 4
В зависимости от вида области допустимых решений и относительного положения линии уровня возможны случаи, показанные на рис.1.2.
Области допустимых решений, изображённые на рис.1.2, а) и 1.2, б) – выпуклые многоугольники. На рис.1.2, а) максимум достигается в одной точке, задача имеет единственное решение (максимизирует z). На рис.1.2, б) задача имеет альтернативный оптимум, максимум z достигается в любой точке отрезка АВ, так как соотношения коэффициентов при неизвестных x1 и x2 в одном из ограничений и в целевой функции совпадают.
Примечание.
При построении z =6.
Рис. 1.1.
На рис.1.2, в) и 1.2, г) представлен случай, когда область допустимых решений – неограниченная фигура. В зависимости от вида z целевая функция достигает минимума в точке «В» (рис.1.2, в) и не имеет максимума (zmax ® ¥) или (рис.1.2, г) оказывается неограниченной сверху и снизу (zmax ® ¥; zmin ® - ¥).
Итак, если оптимальное решение задачи существует, то оно достигается по крайней мере в одной из вершин области допустимых решений.
Заметим, что при практической постановке оптимизационных задач варианты в) и г) указывают на ошибку в построении объекта, так как физические, технические, экономические, временные ограничения на ресурсы не позволяют безгранично увеличивать эффективность реальной системы. Вариант б) вполне реален, например, при максимизации прибыли, получаемой при выпуске изделий, для которых нормы прибыли и нормы времени имеют одинаковое соотношение. Ограничены суммарные затраты времени для лимитирующего производственного участка (станка).
Графический способ решения (перемещение графика целевой функции по симплексу) приемлем только для двухмерных задач (задач на плоскости). Но геометрическое толкование задачи линейного программирования справедливо и для общего случая (m ограничений и n переменных). Каждое из соответствующих неравенству уравнений системы определяет некоторую гиперплоскость в n – мерном пространстве. Множество неотрицательных решений образует выпуклый многогранник в n – мерном пространстве. Линейная форма z -гиперплоскость, перемещая которую параллельно самой себе, будем получать множество точек пересечения её с выпуклым многогранником. Максимальное или минимальное значение линейной формы z достигается в точках, являющихся вершинами выпуклого многогранника.
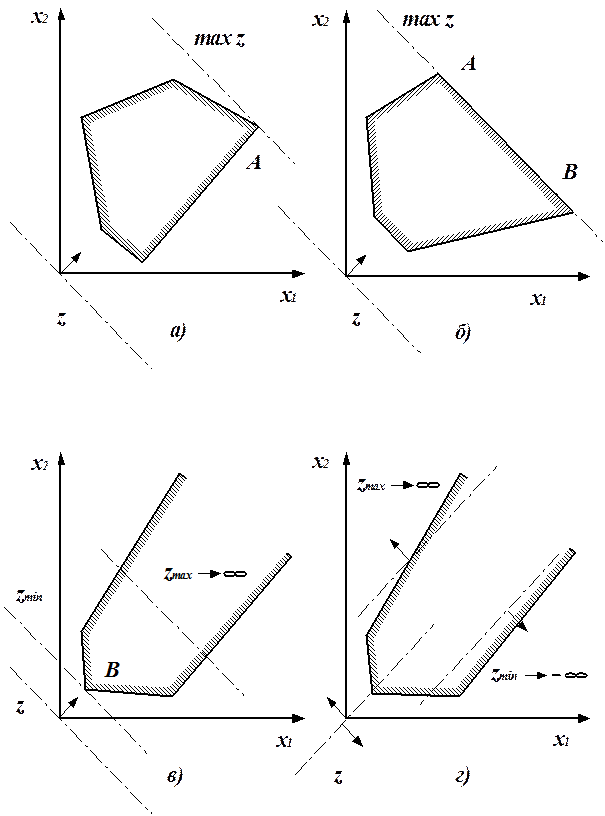
Рис. 1.2