
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Каноническая форма представления ограничений. Допустимые базисные решения.
|
|
Для решения задачи линейного программирования симплекс-методом применяется специальный аппарат формальных преобразований математической модели. Рассмотрим некоторые его положения. Пусть задана основная задача линейного программирования (см. (0.1) и (0.2)). Введя в левую часть каждого неравенства добавочную переменную, преобразуем его в уравнение и перейдём к другой, стандартной форме записи:
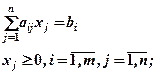 (2.1)
(2.1)
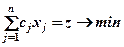 (2.2)
(2.2)
При этом значения bi должны быть неотрицательными. В случае bi < 0 обе части уравнения умножают на ”- 1”. Заметим, что при максимизации z задача сводится к стандартной путём замены: max z = - min (- z).
Систему (2.1) после несложных преобразований можно привести к виду:
 (2.3)
(2.3)
Здесь bi ³ 0. Коэффициенты при переменных 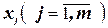 равны единице (+1). Данная система представлена в канонической форме записи. Если количество переменных превышает количество уравнений, то существует бесчисленное множество решений системы.
равны единице (+1). Данная система представлена в канонической форме записи. Если количество переменных превышает количество уравнений, то существует бесчисленное множество решений системы.
Пусть m < n. Разделим все переменные системы (2.3) на две части:
а) основные переменные, количество которых должно быть равно количеству линейно-независимых переменных (m);
б) неосновные переменные, количество которых будет равно n – m.
Назначим первые m переменных (x1, x2, …, xm) в качестве основных. Тогда систему (2.3) можно решить относительно x1, x2, …, xm, если определитель m-го порядка, составленный из коэффициентов при переменных x1, x2, …, xm не равен нулю (Д ¹ 0).
Придавая неосновным (независимым) переменным произвольные числовые значения, получим некоторое решение данной системы, причём каждому набору значений независимых переменных будет соответствовать одно определённое решение системы.
Основные (зависимые, несвободные) переменные будем называть базисными, неосновные (независимые, свободные) – небазисными переменными.
Можно составить бесчисленное множество различных наборов значений независимых переменных. Из всех этих решений в линейном программировании нас будет интересовать так называемые допустимые базисные решения.
Допустимое базисное решение системы линейных уравнений при m < n – это такое решение, в котором неосновным (независимым, небазисным) переменным даны нулевые значения, а значения базисных переменных являются неотрицательными (решение на грани или вершине симплекса, см. рис.1.2.а) и б)).
В теории линейного программирования доказывается, что если оптимальное решение задачи существует, то оно совпадает по крайней мере с одним из допустимых базисных решений.
Поиск и направленные переходы от одних допустимых базисных решений к другим с целью определения оптимального решения может быть выполнен численным методом. Один из них рассмотрим ниже.