
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод множественной корреляции
|
|
В практической работе часто возникает необходимость определить количественное влияние множества факторов, действующих одновременно или в отдельности. В таких случаях используют методы множественной корреляции, которые позволяют исследовать статистические зависимости результативного признака от нескольких факториальных.
При использовании методов множественной корреляции составляют многофакторные статистические модели, сущность которых состоит в получении уравнений множественной регрессии. Однако прежде чем рассчитывать уравнение множественной регрессии и определять его коэффициенты, необходимо установить вид этого уравнения. Ту или иную форму многофакторной связи необходимо выбирать с учетом некоторых условий:
- выбранная функция должна отражать закономерности, существующие между признаками, принятыми для многофакторного исследования;
- аналитическое уравнение многофакторной связи, используемое в качестве аппроксимирующей функции, должно иметь по возможности простой вид;
- число факторов, включаемых в модели, должно быть ограничено, чтобы модели были удобны в практической работе.
Взаимосвязь между признаками, состоящая в изменении средней величины одного из них в зависимости от значения другого, называется корреляцией. Слово «корреляция» происходит от английского relation и означает соотношение или соответствие между факторами и признаками. Термин корреляция применяется в различных областях науки и техники для обозначения взаимозависимости, взаимного соответствия. Посредством корреляции можно определить числовое значение влияния каждого из множества анализируемых факторов, действующих совместно на одну из сторон процесса и взаимосвязанных между собой.
Статистические методы и теория корреляции позволяют понять происхождение конкретного явления, вскрыть составляющие его факторы, изучить процесс формирования явления не только в качественной, но и в количественной форме и выразить его статистической моделью.
Методы теории корреляции позволяют устанавливать взаимосвязь изучаемых факторов без учета влияния случайных. При решении конкретных задач этими методами говорят о наличии коррелированных величин, т. е. таких, которые связаны друг с другом корреляционной связью.
При выполнении корреляционных расчетов необходимо различать факториальный и результативный признаки. Факториальным называется такой признак, от которого зависит другой признак, а он сам является независимым. В отличие от него зависимый признак называется результативным. В процессе формализации статистической модели факториальный признак обозначается через х, а результативный - через у, т. е. условно можно сказать, что факториальный признак выражает аргумент, а результативный - функцию. В статистических исследованиях, выполняемых с помощью методов корреляционного анализа, возможны случаи, когда один и тот же признак в различных статистических совокупностях выступает в качестве результативного и факториального. Это значит, что определение результативного и факториального признаков не является раз и навсегда законченным процессом, напротив, он зависит от конкретных условий изучения взаимосвязей различных факторов.
В процессе корреляционного анализа осуществляется исследование связей, которое состоит из совокупности методов и приемов по выявлению, изучению и количественной оценке взаимосвязей между результативными и факториальными признаками. Среди них наиболее простым является метод группировок, основанный на выявлении различий между групповыми средними.
Связь между показателями и факторами часто выражается корреляционной зависимостью, сущность которой состоит в том, что на величину результативного признака оказывают влияние не только факториальный, а множество случайных признаков, изолировать которые не представляется возможным. Если при исследовании явлений или их признаков наблюдаются изменения характеристик распределения одного из них под воздействием другого, то говорят о наличии статистической связи. Эти связи характеризуются тем, что в них результативный признак определяется влиянием не только факториального признака. В отличие от функциональных корреляционные связи не являются причинно-следственными, а бывают вероятностными или стохастическими. Стохастические связи проявляются между случайными величинами и наблюдаются обычно тогда, когда наряду с общими случайными факторами, влияющими как на одну, так и на другую величину, имеются еще и другие случайные факторы, не одинаковые для обеих величин.
В зависимости от постановки задачи и статистических методов, используемых для ее решения, различают парную и множественную корреляцию. Парная корреляция устанавливает количественную взаимосвязь между парой признаков, один из которых является факториальным, а другой — результативным. Множественная корреляция определяет взаимосвязь между множеством признаков и поэтому в отличие от парной характеризуется множеством факториальных признаков.
Для того, чтобы проанализировать статистический материал и сделать соответствующие выводы, необходимо привести в определенный порядок или систематизировать исходные данные. Первоначально статистический материал систематизируется по одному качественному признаку путем построения ряда распределения и расчета его статистических характеристик.
Если необходимо одновременно проанализировать статистический материал, характеризующий те или иные экономические явления по двум или большему числу признаков, то используют методы корреляции, которые позволяют установить корреляционную зависимость между факторами. С увеличением числа единиц статистической совокупности появляется возможность выявить определенные закономерности, присущие анализируемым процессам и явлениям, которые трудно установить при изучении незначительного числа наблюдений. В этом проявляется действие закона больших чисел. Таким образом, если отдельные единицы статистической совокупности находятся в некоторых общих условиях, то на их основе можно установить закономерность из совокупного действия большого числа, случайных факторов.
Проведение научных исследований, решений технических, организационных, экономических и других задач неразрывно связано с опытами или массовыми процессами и явлениями, которые многократно повторяются при наличии некоторых весьма общих условий. Однако как бы тщательно ни готовились опыты, их результаты в той или иной степени отличаются друг от друга. Это связано с тем, что условия проведения опытов изменяются под влиянием многочисленных случайных факторов, которые не поддаются контролю и колеблются от одного измерения к другому. Если эти колебания невелики и отражаются лишь на точности расчетов, то ими можно пренебречь и с некоторым приближением рассматривать как функциональную зависимость. При исследовании функциональной зависимости, как правило, удается изолировать влияние случайных факторов. В некоторых же исследованиях практически невозможно устранить влияние побочных факторов, так как сама постановка эксперимента обычно невозможна. В этих условиях определяются корреляционные связи. При корреляционной зависимости, в отличие от функциональной, каждому значению аргумента соответствует ряд распределения функции, и с изменением аргумента эти ряды изменяются.
Первая и основная задача, которую решает теория корреляции, - это измерение связи. Сущность ее заключается в том, чтобы на основе наблюдения над большим статистическим материалом выяснить, как изменяется функция при изменении одного аргумента и неизменности остальных. В действительности влияние побочных факторов устранить не удается.
Изучение статистических зависимостей основывается на исследовании таких связей между случайными переменными, при которых различные значения принимает другая случайная переменная. Зная статистическую зависимость между случайными переменными, можно прогнозировать значение зависимой случайной переменной в предположении, что независимая переменная примет определенное значение.
Метод, позволяющий по выборке, которая содержит отдельные наблюдавшиеся значения неизвестных параметров а0, а1… аn называется множественной регрессией, а полученное выражение – уравнением множественной регрессии.
Зависимость между одной случайной переменной и условным средним значением другой случайной переменной называется корреляционной зависимостью. Она характеризуется формой и теснотой связи. Форма связи – это вид математической связи между случайными величинами, характеризуется функцией регрессии (линейная, квадратная, показательная и т.д.).
Для характеристики формы связи пользуются понятием кривой регрессии – это условное среднее значение случайной переменной Y, рассматриваемой как функция от Х, то есть 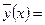
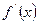 .
.
Графической формой систематизации статистического материала по двум качественным признакам является поле корреляции. Для его построения необходимо определить, какой из признаков является факториальным, а какой — результативным. По нему можно в первом приближении сделать вывод о форме и тесноте связи. Такая линия называется эмпирической линией регрессии. Теснота связи между случайными величинами оценивается по коэффициенту корреляции.
На основе выявленной формы между признаками рассчитывают параметры уравнения множественной регрессии. Для их получения можно использовать два способа: способ парных коэффициентов корреляции и способ наименьших квадратов. Однако такое выделение двух способов несколько условно, так как в обоих случаях используется метод наименьших квадратов. В первом случае коэффициенты уравнения множественной регрессии рассчитываются по методу наименьших квадратов через парные коэффициенты корреляции rу/х и находятся стандартизованные коэффициенты регрессии β j, во втором случае - по способу наименьших квадратов через переменные у и х находятся коэффициенты регрессии в натуральных единицах наблюдения в виде aj.. Первый способ является наиболее трудоемким, но он дает полный материал для анализа изучаемых зависимостей. Второй способ менее трудоемок, однако на его основе можно получить лишь коэффициенты уравнения регрессии aj и совокупный коэффициент корреляции R. Коэффициенты же парной корреляции rу/х здесь получить не удается.
В области технологии строительного производства и технологии изготовления строительных материалов на заводах стройиндустрии методы корреляционного анализа используются для решения задач, связанных с изучением массовых закономерностей производственного процесса в целях его оптимизации, повышения качества и надежности продукции.
Статистические методы контроля качества продукции нашли широкое применение в практике работы промышленных предприятий, производящих строительные материалы, детали, конструкции и полуфабрикаты. Использование методов парной и множественной корреляции при изучении технологических процессов позволяет определять оптимальные характеристики этих процессов. Например, исследуя влияние различных факторов технологического процесса приготовления бетона на его качество и прочность, можно установить статистическими методами оптимальное соотношение между процентным содержанием воды, песка и цемента в замесе с учетом температуры смеси и средней температурой среды хранения бетона. Эти же методы позволяют осуществлять статистический анализ различных способов бетонирования в зимних условиях: методом «термоса»; с применением добавок - ускорителей твердения бетона; с предварительным электро- или пароразогревом бетонной смеси; с использованием быстротвердеющих цементов с повышенным тепловыделением; укладкой бетонов с противоморозными добавками, твердеющими при отрицательных температурах; с искусственным прогревом и обогревом бетона с помощью электрической энергии, пара или теплого воздуха (кратковременный нагрев, периферийный электропрогрев, греющие опалубки, электропрогрев нашивными электродами, индукционный метод обогрева, инфракрасный обогрев) и т. д.
Методы регрессионного анализа дают возможность выполнить комплексное исследование влияния различных способов зимнего бетонирования на стоимость бетонных работ исходя из модуля поверхности конструкций наружной температуры воздуха, марки применяемого цемента и других технологических параметров и таким путем определить величину зимних удорожаний в зависимости от методов производства бетонных работ.
Применительно к деятельности заводов строительной индустрии особенно пригодны статистические методы контроля качества продукции. Здесь применимы выборочные методы контроля. Для этого проводится выборка изделий из всей совокупности с целью исследовать качество продукции в отобранной части и сделать вывод о качестве продукции всей партии. Наряду с этим выборка используется для контроля за ходом самого производственного процесса и недопущения выпуска бракованных изделий. В этом случае выборочное наблюдение имеет целью профилактику брака, т. е. недопущение в дальнейшем процессе производства брака при его обнаружении или возможности его появления.
Таким образом, технологическая статистика, изучающая технический прогресс и статистические закономерности, наблюдаемые в технологических процессах, широко использует метод корреляции [11].
Статистическое планирование эксперимента
Понятие о планировании эксперимента. Основные задачи эксперимента
Во многих областях науки и техники, в том числе и в строительстве, исследование того или иного явления или процесса возможно только эмпирически, то есть с помощью опыта или эксперимента.
Одной из наиболее часто встречающихся проблем, встающих перед учеными различных специальностей, является проблема нахождения зависимости между некоторым набором величин.Эта зависимость может быть выведена из теории и (или) может быть получена на основании экспериментальных исследований. Если зависимость выведена из теоретических соображений, то довольно часто она может быть приближенно представлена в аналитическом виде, заданном с точностью до нескольких неизвестных параметров. Если же в основе построения зависимости лежат экспериментальные исследования, то параметрическая зависимость постулируется. В обоих случаях при построении математической модели должны использоваться сведения об исследуемом объекте, на основании которых мог бы быть сделан вывод о достаточной точности описания объекта моделью и, следовательно, о том, что приведенные для модели статистические выводы в определенной мере справедливы и по отношению к самому объекту.
Результаты в области планирования эксперимента имеют очевидное прикладное значение. Дорогостоящие эксперименты, а также эксперименты, которые невозможно воспроизвести повторно, требуют предварительного квалифицированного планирования. С развитием ЭВМ практически любые затраты на численное построение планов могут оказаться оправданными. Различные разделы теории планирования эксперимента в настоящее время развиты существенно в разной степени, но практические потребности требуют активной разработки всех разделов.
Результатом эксперимента является получение числовых значений выходного параметра y в зависимости от конкретных значений входных параметров (факторов) х1, х2, …, хk. При этом изначально внутренняя структура функционирования процесса неизвестна. Известны лишь входы хi и выход у. Каждый эксперимент требует обработки.
Входные и выходные параметры по своей природе являются случайными величинами. Следовательно, при обработке экспериментальных данных нужно пользоваться методами математической статистики. Многие эксперименты являются сложными и дорогостоящими, поэтому необходимо применение методов, которые давали бы не только способ обработки экспериментальных данных, но и позволяли бы оптимальным образом организовать эксперимент.
В результате проведения эксперимента возникают следующие основные задачи.
1 Первичная статистическая обработка результатов эксперимента. Если результат эксперимента зависит от случая, то эксперимент называют статистическим. При описании такого эксперимента применяются средства и термины теории вероятностей и математической статистики. Для этого определяют средние значения выходного параметра при многократном повторении одного и того же набора входных параметров и разброс вокруг этого среднего значения, т. е. дисперсию и среднеквадратическое отклонение.
2 Обоснование точности полученных экспериментально данных, в том числе средних значений выходного параметра и среднеквадратических отклонений, а так же числа повторений наборов входных параметров. Для этого используются доверительный интервал и критерии согласия.
3 Определение аналитической зависимости выходного параметра у от входных параметров х1, х2, …, хk.
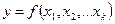 (4.1)
(4.1)
т. е. математической модели изучаемого процесса. Эта аналитическая зависимость называется функцией отклика. Для её получения применяют метод наименьших квадратов.
4 Планирование эксперимента, т. е. выбор наилучшего эксперимента с позиции затрат материальных ресурсов и точности описания процесса.
Кроме того, может оказаться, что некоторые входные параметры мало влияют на выходной параметр и их можно исключить из рассмотрения. Выяснить, зависимы ли случайные величины хi и у можно, если определить корреляционную зависимость между этими случайными величинами, найдя, например, коэффициент корреляции между случайными величинами хi и у.
Существует два основных метода эмпирического исследования: наблюдение и эксперимент. Наблюдение – целенаправленное восприятие объекта без активного вмешательства в его поведение. Исследователь вынужден пассивно ожидать естественного проявления необходимых эффектов в поведении объекта, что значительно удлиняет ожидаемое время сбора информации. Например, фиксация температуры, давления, реакции химических продуктов в агрегате при нормальном режиме работы. Однако, как бы удачно не было бы организовано наблюдение, оно как опыт не может преодолеть своей ограниченности, вытекающей из пассивности наблюдателя по отношению к объекту исследования. Намного более по качеству и по объему информацию можно получить из эксперимента. Под экспериментом понимают вид деятельности, предпринимаемой в целях научного познания, открытия объективных закономерностей и состоящей в воздействии на изучаемый объект (процесс) посредством специальных инструментов и приборов, благодаря чему удается:
- устранить, изолировать изучаемое явление от побочных, несущественных и затемняющих его сущность явлений и изучать его в чистом виде;
- многократно воспроизводить ход процесса в строго фиксированных, поддающихся контролю условиях;
- планомерно изменять, варьировать, комбинировать различные условия в целях получения искомого результата.
Эксперимент всегда должен планироваться исследователем. Некоторые из этапов исследования могут быть достаточно формализованы и даже стандартизированы на основе математической теории эксперимента, которая различает два принципа постановки экспериментов: пассивный и активный. При пассивном эксперименте расположение опытных точек в факторном пространстве ведется на интуитивном уровне без предварительного учета методов дальнейшей математической обработки информации. Интуитивный план эксперимента в той или иной степени отражает предшествующий опыт, однако по мере роста числа факторов (xi) задача интуитивного планирования настолько усложняется, что экспериментальные точки располагаются лишь по некоторым сечениям пространства, выбранным весьма бессистемно. Эта особенность интуитивного планирования экспериментов (и наблюдений) резко усложняет вычислительные процедуры, а также затрудняет практическое использование моделей и их технико-экономическую интерпретацию. Информация, собранная при активном эксперименте по математически обоснованному плану, учитывающему цели эксперимента и методы обработки его результатов, имеет большую информационную ценность. При этом практически всегда меньше и затраты ресурсов (материальных и временных), чем на пассивный эксперимент. Интуитивное расположение точек в факторном пространстве заменяется алгоритмизированным, которое в некотором смысле оптимально. Оптимальность планирования обеспечивается предшествующим проведению эксперимента исследованием свойств матрицы входных факторов [x]. Особенно важно то, что число «активных» экспериментов сокращается по сравнению с традиционными методиками в 2-10 раз, причем достоверность информации не ухудшается, а в ряде случаев и увеличивается, кроме того, преимущество активных экспериментов заключается в следующем:
- оптимальное использование факторного пространства;
- введение четкой логики для всех процедур, последовательно совершаемых экспериментатором;
- рандомизация условий опытов, когда многочисленные мешающие факторы превращаются в случайные величины;
- выполнение исходных предпосылок регрессионного анализа, а это зачастую исключено при пассивном эксперименте (в результате числовые оценки коэффициентов в моделях оказываются смещенными);
- оценку элемента неопределенности, связанного с экспериментом, что дает возможность сопоставить результаты, полученные разными исследованиями;
- экспериментатор дает количественные оценки, абстрагируясь от сложных и плохо изученных явлений, происходящих в системе;
- для математического описания исследуемого процесса планируется минимальное количество опытов, из которых информация извлекается с максимальной полнотой, что позволяет значительно уменьшить трудоемкость опытных работ;
- опыты ставятся небольшими сериями по некоторому оптимальному плану, что исключает слепой хаотический поиск;
- упрощаются вычисления.
В связи с планированием принято выделять следующие типы эксперимента. Классификация экспериментов довольно разнообразна. Для нас далее будут представлять интерес эксперименты, которые можно планировать.
Экстремальный эксперимент, задача которого состоит в определении экстремальных значений функции регрессии (или комбинации факторов, при которых функция отклика принимает экстремальные значения). Методы его планирования тесно связаны с методами планирования регрессионного и факторного экспериментов, с одной стороны, и методами стохастического программирования, с другой.
Эксперимент по проверке конкретной статистической гипотезы (дискриминирующий эксперимент). Это сравнительно изученный раздел, который также связан с планированием в регрессионных и факторных моделях.
Отсеивающий эксперимент, задача которого состоит в выделении значимых факторов. Теория его планирования активно развивается в последнем десятилетии.
Имитированный эксперимент, который, как правило, связан с имитацией изучаемого явления на ЭВМ или другом устройстве, позволяющем воспроизводить это явление с приемлемой точностью. Имитационный эксперимент направлен не на изучение природы, а на изучение достаточно сложной (имитационной) модели. Ряд результатов по его планированию получен в связи с использованием метода Монте-Карло, а также исследованием сложных систем (типа моделей ядерного реактора) [16].
Перечисленные типы не исчерпывают всего многообразия экспериментальных ситуаций, но для них имеются математические модели и методы. Развитие методов анализа этих моделей позволяет, как правило, формулировать и исследовать задачи планирования эксперимента в более сложных ситуациях.
Не всякий эксперимент следует относить к числу статистических. Прежде всего, следуетвыделить класс экспериментов, где влияние случая пренебрежимо. И хотя формально результаты, полученные для статистических моделей, справедливы и для детерминированных, постановки задач и методы исследования здесь другие. Можно выделить также экспериментальные ситуации, в которых об ошибке измерений известно, что она не превосходит заданной величины, но невозможно получить сведения об её распределении. Здесь методы исследования также могут быть не связаны с теорией вероятностей. Наконец, можно упомянуть о нечетком задании условий эксперимента.