
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 5.4 Детерминированный автомат
|
|
Пример: Рассмотрим ситуацию, встречающуюся в народных сказках. Иванушка-дурачок встречает свадьбу. И начинает громко причитать и плакать. Такое неадекватное поведение вызывает мгновенную реакцию среды. Жестоко побитый Иванушка через некоторое время встречает похороны. Помня свою неудачу, он начинает весело смеяться и петь. И снова жестокая кара постигает нашего простодушного героя. Он снова бит.

Нарисуем граф переходов этого автомата. Состояние 1 – плясать, состояние 2 – плакать. Наша среда так же может вы давать только две ответные реакции: «Бить» или «Не бить». Сплошной чертой мы обозначим реакцию нашего автомата на поощрение (реакция «Не бить»); пунктирной линией – на наказание (реакция «Бить»).
Составим для этого примера таблицу переходов.
Строки – это состояние автомата, в момент времени t
U –это состояние окружающей среды. Обе эти переменные двоичны.
| 1 (свадьба) | 0 (похороны) | |
| 1 (плакать) | ||
| 2 (петь) |
Значения переменной Х – " 1" – плакать
" 2" - петь
Значения переменной U – " 0" – похороны
" 1" - свадьба
Выходом этого автомата будем считать сведения о смене состояния автомата. " 0" – если не меняет состояние
" 1" – если меняет.
Анализируя нелегкую судьбу Иванушки, сразу возникает идея, что его поведение будет более адекватным, если Иванушка, принимая решение, будет основываться на данных нескольких последних событий, т.е. будет обладать памятью.

Вот как выглядит граф переходов такого автомата. Сплошной стрелкой мы показали переход при наказании, пунктирной – при поощрении. В нашем примере определено по три устойчивых состояния для каждого действия автомата. Будем считать, что состояния 1, 2, 3 – обозначают действие «плакать» нашего Иванушки, а состояния 4, 5, 6 – действие «петь». Это число называется глубиной памяти конечного автомата или степенью его инерционности. Покажем, что такой автомат достаточно быстро найдет лучшее для статической среды действие, и будет выполнять только его. Поясним эту мысль. Пусть в начале наш автомат находится в состоянии 3. А влияние среды описывается (0, 9; 0, 1) т.е. с вероятностью 0, 9 встретится свадьба и с вероятностью 0, 1 – похороны. Понаблюдаем за поведением нашего Иванушки. С вероятностью 0, 9 встретится свадьба, и Ивана побьют, он перейдет в состояние 4, он станет петь и опять с вероятностью 0, 9 на свадьбе. По теории вероятностей, вероятность получения от среды двух свадеб подряд равна 0, 81, Двух похорон подряд 0, 01, а вероятность одной свадьбы и одних похорон = 0, 18. Следовательно, после двух тактов взаимодействия с вероятностью 0, 01 автомат окажется в состоянии 1, с Р=0, 18 в прежнем положении, и с Р=0.81 в состоянии 5. С ростом числа взаимодействий качественно картина не изменится. Вероятность покинуть группу 6-4 неуклонно падает, а вероятность остаться в ней – растет.
Что произойдет дальше? С Р=0, 9 наш автомат получит поощрение и перейдет в состояние 6 и т.д. Вероятность покинуть группу 4-6 все время будет уменьшаться. Этот процесс очень похож на процесс обучения, после которого наш автомат " достаточно адекватно" ведет себя в данной статической среде. " Достаточно адекватно" потому, что существует очень малая, но ненулевая вероятность покинуть группу наиболее благоприятного поведения (т.е. поведения когда сумма штрафов минимальна).
Если же среда динамическая, то существует зависимость, между вероятностью смены законов среды и глубиной памяти автомата. Это утверждение интуитивно понятно, ведь в динамическом мире смена ситуаций происходит с большой частотой, и инерционность вряд ли может служить хорошим средством для существования в этом мире. Экспериментально показано, что для каждого динамического мира нужна своя наилучшая глубина памяти, выбранная в зависимости от скорости изменения обстановки, а не по принципу «Чем больше, тем лучше». Такая глубина памяти называется оптимальной.
Все сказанное выше, справедливо и для автомата, у которого больше двух действий и больше двух состояний среды. Чем больше глубина памяти такого автомата, тем целесообразнее его поведение. Рассмотренный нами автомат называется автоматом с линейной тактикой.
Подчеркнем еще раз, повышение глубины памяти улучшает показатель целесообразности поведения автомата с линейной тактикой для статических сред. Более того, Цетлин показал, что если min Pi < 0, 5 то при увеличении глубины памяти q автомата с линейной тактикой мы получим последовательность автоматов с линейной тактикой со все увеличивающейся глубиной памяти, которая является асимптотически оптимальной. Это означает, что при q → ∞ М(q, Е) → Мmin – минимальный суммарный штраф. Т.о. конструкция, предложенная Цетлиным, обеспечивает при достаточно больших значения q поведение, сколь угодно близкое к наилучшему в любых стационарных случайных средах.
Рассмотрим еще пару конструкция автоматов с линейной тактикой.
Эта конструкция предложена В.И. Кринским. Мы будем называть «доверчивым». Вот как выглядит его граф переходов.
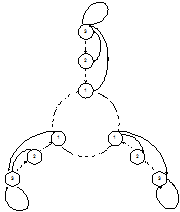 |
При поступлении сигнала штраф, поведение этого автомата аналогично поведению автомата с линейной тактикой Цетлина, но при получении сигнала поощрения, этот автомат, независимо в каком состоянии лепестка он находился в данный момент, переходит в самое глубокое состояние данного лепестка. Этот автомат, как будто, склонен верить в хорошее, и положительный сигнал среды приводит его в состояние «эйфории».
Строго доказано, что автоматы Кринского ведут себя целесообразно в любых стационарных случайных средах.
Может сложиться ощущение, что любые меры по увеличению числа инерционности автомата, улучшает показатель целесообразности поведения автомата.
Ситуация качественно меняется, если наш линейный автомат имеет дело с динамической средой. Если смена сред происходит достаточно быстро, то инерционность вряд ли может служить хорошим средством для существования в этом мире. Ведь в динамическом мире надо быстро следить за возникающими изменениями среды, и для любого динамического мира необходима своя глубина памяти, выбранная в зависимости от скорости изменения обстановки.