
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 5.6 Автомат с переменной структурой
|
|
Для начала рассмотрим такую ситуацию. Предположим, что вы на своей машине ежедневно добираетесь от дома до работы. В вашем распоряжении есть два возможных маршрута, и вы вольны выбрать любой из них. Т.к. вы всегда выезжаете в одно и то же время, то обстановка по каждому из маршрутов как бы стационарна. И анализируя эту обстановку, вы убедились, что один из маршрутов лучше другого: времени тратиться меньше – движение здесь менее интенсивное, чем по другому маршруту, да и светофоров здесь не так много. Но вот беда: время от времени из-за каких-то ремонтных работ скорость движения здесь резко снижается, образуются пробки, и можно потерять много времени пока они ликвидируются. В этих условиях данный маршрут становится намного хуже другого. Вы бы потеряли куда меньше времени, выбрав в эти неудачные дни другой маршрут. Если нет никакой информации о частоте ремонтных работ на трассе первого маршрута, то выезжая из дома нет никаких шансов угадать, по какому маршруту лучше сегодня ехать. Однако, день за днем, вы накапливаете информацию. Учитесь на своем горьком опыте. Выясняется, что чаще всего пробки образуются в среду и пятницу и вероятность этих пробок достаточно велика. Тогда выбирая в остальные дни недели первый маршрут, вы в среду и пятницу без колебаний выбираете менее хороший маршрут поездки.
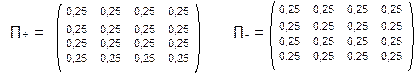 |
Но ни автомат с линейной структурой, ни вероятностный автомат Крылова не могут приспособиться к часто меняющейся динамической среде, поскольку его таблицы переходов не меняются в процессе функционирования. Поэтому рассмотрим модель автомата с переменной структурой. Это уже знакомый нам вероятностный автомат в начале функционирования находящийся в безличном состоянии, с наперед заданными вероятностями переходов.
Если, выполнив какое-то действие, автомат получил сигнал штраф, то в матрице переходов он уменьшает значение вероятности этого перехода на заданную величину D, но сумма всех элементов строк должна быть равна 1, поэтому все ненулевые элементы строки необходимо изменить на величину D/h, где h – количество ненулевых элементов строки.
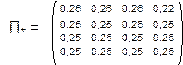 |
Пусть для определенности в начальный момент времени автомат находился в состоянии 1, и совершил действие 1, соответствующее этому состоянию. С помощью равновероятного выбора по матрице П+ перешел в состояние 4. И пусть после этого он получил сигнал штраф. Получение такого сигнала заставляет автомат считать свой переход 1 – 4 ошибкой. Эта информация фиксируется следующим образом. Вероятность П+14 уменьшается на D, а все остальные элементы строки увеличиваются на D/3. Для удобства положим D = 0.03. Тогда после этого шага матрица П- не изменится, а матрица П+ будет выглядеть так:
На очередном шаге автомат делает действие 2, соответствующее состоянию 4, и выбирает очередное состояние на основании матрицы П- (т.к. в текущем акте общения со средой он находится в условиях последнего сигнала от среды – штрафа).
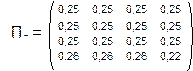 |
Пусть он выбрал переход 4 – 4 и вновь получил штраф. Теперь меняется матрица П-, а матрица П+ остается неизменной.
Так постепенно происходит перестройка матриц П+ и П- в зависимости от сигналов, формируемых средой. Для автоматов с переменной структурой экспериментально показан следующий фундаментальный результат: с течением времени функционирование автомата с переменной структурой в переключающихся средах, а которых автомат с линейной тактикой ведет себя целесообразно, неограниченно приближается к поведению автомата линейной структурой с оптимальной глубиной памяти. Другими словами, автомат с переменной структурой сам находит оптимальную глубину памяти. Это весьма важно, т.к. значение оптимальной глубины памяти нельзя определить аналитически, оно подбирается в процессе функционирования в среде.
Рассмотрением этой конструкции автомата мы и ограничимся.
Скажем только, что существует очень большое множество классов конечных и бесконечных автоматов, активно используемых в технике. И более подробно об этих объектах вы будете говорить в курсах теории автоматического управления. Я же хочу обобщить сказанное. С математической точки зрения автомат задается А – входным алфавитом, В – выходным алфавитом, S – алфавитом состояний автомата и двумя функциями j - функцией переходов и J - функцией выходов.
Напомню, что под алфавитом понимается множество возможных значений. j и J могут быть и произвольными отношениями и вероятностными функциями.
Следует четко понимать, что функция j отображает множество SxА в S; а J - отображает множество SxА в В.