
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие многомерной выборки
|
|
Если при статистических наблюдениях для каждого объекта измеряют значения 2-х, 3-х, …, n признаков, то в этом случае получают 2-х, 3-х, …, n-мерные выборки.
При n 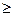 2 выборки называют многомерными.
2 выборки называют многомерными.
Каждый элемент многомерной выборки состоит из 2-х, 3-х, …, n чисел.
При обработке многомерных выборок, помимо изучения статистического материала, относящегося к отдельным признакам, стремятся также установить связи между признаками.
Рассмотрим выборку из двумерной генеральной совокупности, отождествляемой с системой 2-х СВ (X, Y).
В результате n независимых наблюдений получим n пар чисел:
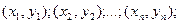 (6)
(6)
Обычно статистический материал сводят в так называемую корреляционную таблицу:
Таблица 2.


| Y X | 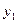
| 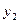
| … | 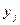
| … | 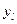
| 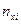
|
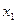
| 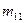
| 
| … | 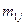
| … | 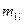
| 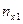
|
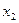
| 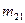
| 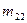
| … | 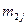
| … | 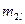
| 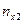
|
| … | … | … | … | … | … | … | … |
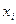
| 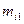
| 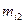
| … | 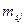
| … | 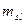
| 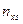
|
| … | … | … | … | … | … | … | … |
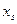
| 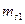
| 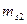
| … | 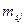
| … | 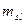
| 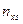
|
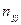
| 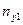
| 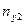
| … | 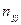
| … | 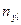
| 
|

где: 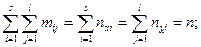
На пересечении строк и столбцов частоты (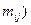 наблюденных пар значений признаков (
наблюденных пар значений признаков (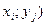 :
:
n – объем выборки;
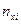 - число пар (
- число пар (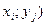 при всех
при всех 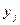
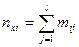 (7)
(7)
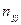 - число пар (
- число пар (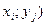 при всех
при всех 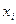
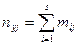 (8)
(8)
Корреляционная таблица позволяет рассчитать числовые характеристики выборки по формулам:
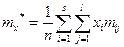 (9)
(9)
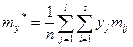 (10)
(10)
где 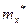 и
и 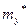 - выборочные средние признаков X и Y.
- выборочные средние признаков X и Y.
Если корреляционная таблица содержит предварительно вычисленные по формулам (7), (8) 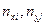 (см. Таблицу 2), то выражения (9), (10) для нахождения
(см. Таблицу 2), то выражения (9), (10) для нахождения 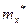 и
и 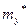 могут быть упрощены:
могут быть упрощены:
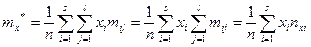
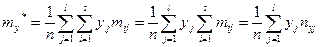
т. е.
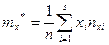 (9.1)
(9.1)
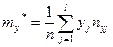 (10.1)
(10.1)
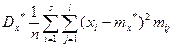 (11)
(11)
 , (12)
, (12)
где 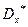 и
и 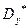 – выборочные дисперсии признаков X и Y.
– выборочные дисперсии признаков X и Y.
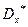 и
и 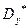
 могут быть вычислены также по формулам:
могут быть вычислены также по формулам:
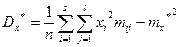 (11.1)
(11.1)
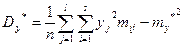 (12.1)
(12.1)
Или, с учетом (7), (8):
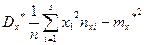 (11.2)
(11.2)
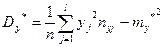 (12.2)
(12.2)
В качестве оценок математических ожиданий 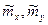 и оценок дисперсий
и оценок дисперсий 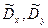 признаков X и Y можно принять:
признаков X и Y можно принять:
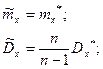
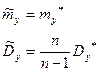 (13)
(13)
Выборочные корреляционные моменты определяются по формулам:
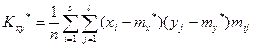 (14)
(14)
или
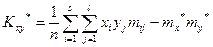 (15)
(15)
Можно доказать, что для несмещенной оценки корреляционного момента 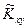 необходим такой же поправочный коэффициент
необходим такой же поправочный коэффициент 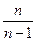 , как и для оценки дисперсии, т.е.
, как и для оценки дисперсии, т.е.
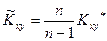 (16)
(16)
Оценка коэффициента корреляции 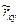 выразится формулой:
выразится формулой:
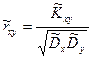 (17)
(17)
Выражая оценки через выборочные характеристики по формулам (13) и (16), получим
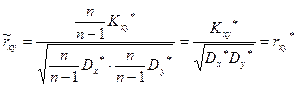 , т. е.
, т. е.
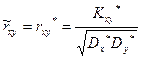 (18)
(18)
где 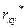 – выборочный коэффициент корреляции.
– выборочный коэффициент корреляции.
1.4. Выборочная функция регрессии
Обратимся к корреляционной таблице (Таблица 2). Каждому варианту 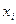 признака (СВ) X можно поставить в соответствие среднее арифметическое
признака (СВ) X можно поставить в соответствие среднее арифметическое 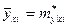 соответствующих ему (входящих с ним в пару) значений признака Y, т.е.
соответствующих ему (входящих с ним в пару) значений признака Y, т.е.
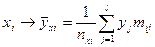 (19)
(19)
Для всех 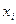 можно найти соответствующее им
можно найти соответствующее им 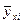 .
.
Величина 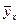 есть не что иное, как условное выборочное среднее – статистический аналог условного математического ожидания, т.е.:
есть не что иное, как условное выборочное среднее – статистический аналог условного математического ожидания, т.е.:
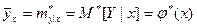 (20)
(20)
Таким образом может быть задана выборочная функция регрессии Y на x.
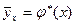 (21)
(21)
При этом функция 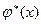 оказывается заданной в табличной форме:
оказывается заданной в табличной форме:
 Таблица 3
Таблица 3
| X | 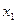
| 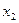
| … | 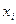
| … | 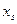
|
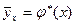
| 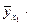
| 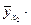
| … | 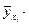
| … | 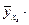
|
Располагая Табл. 3 значений выборочной функции регрессии Y на x, с учетом (19), можно упростить расчетную формулу (15) для вычисления  – выборочного корреляционного момента:
– выборочного корреляционного момента:
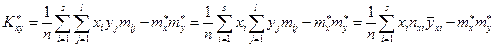 , т.е.
, т.е.
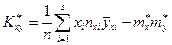 (15.1)
(15.1)
Выборочная функция регрессии X на y может быть найдена аналогично, т.е.:
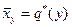 (22)
(22)
Таблица 4
| Y | 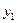
| 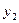
| … | 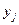
| … | 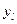
|
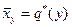
| 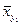
| 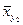
| … | 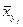
| … | 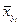 
|
где 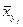 - условное выборочное среднее, вычисляемое по формуле:
- условное выборочное среднее, вычисляемое по формуле:
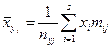 (23)
(23)
Если для функций 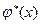 и
и 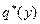 , заданных в табличной форме (см. Таблицы 3 и 4) подобрать аналитические выражения, т.е. решить задачу аппроксимации, то получим новые функции:
, заданных в табличной форме (см. Таблицы 3 и 4) подобрать аналитические выражения, т.е. решить задачу аппроксимации, то получим новые функции:
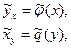 (24)
(24)
которые являются оценками функций регрессии 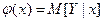 и
и 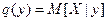 .
.
Будем называть функции 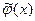 и
и 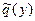 (в отличие от
(в отличие от 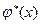 и
и 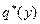 ) - эмпирическими функциями регрессии Y на x и X на y – соответственно.
) - эмпирическими функциями регрессии Y на x и X на y – соответственно.
Для линейной регрессии вид функций 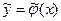 и
и 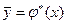 показан на Рисунке 1.
показан на Рисунке 1.
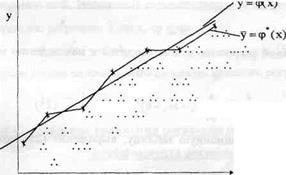
Рис. 1
1.5. Метод наименьших квадратов
Сущность метода наименьших квадратов состоит в выборе линии регрессии таким образом, чтобы сумма квадратов отклонений 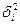 выборочных значений
выборочных значений  от аппроксимирующей функции
от аппроксимирующей функции 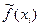 была наименьшей (рис.2).
была наименьшей (рис.2).
|
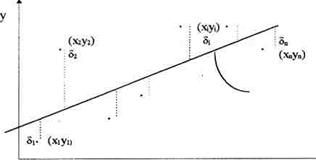
Рис. 2
Для линейной регрессии задача сводится к нахождению минимума функции
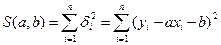 (25)
(25)
Используя корреляционную таблицу, выражение (25) можно переписать в виде:
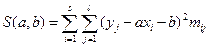 (26)
(26)
Надо подобрать a и b таким образом, чтобы сумма S(a, b) имела наименьшее значение, т.е. a и b должны удовлетворять системе уравнений:
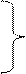
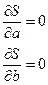 (27)
(27)
Дифференцируя (26) по a и b, систему (27) перепишем:
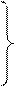
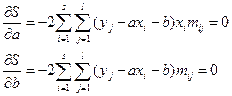 (28)
(28)
После упрощения система (28) примет вид:
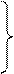
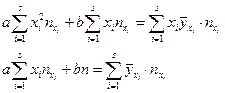 (29)
(29)
Систему линейных алгебраических уравнений (29) иногда называют нормальной. Решая (29) относительно a и b, найдем эмпирическую функцию регрессии Y на x, то есть
 (30)
(30)
Аналогично можно получить эмпирическую функцию регрессии X на y:
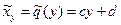 (31)
(31)
1.6. Составление уравнения регрессии путем вычисления коэффициента регрессии.
Для системы линейных алгебраических уравнений (29) найдено решение в общем виде, а именно:
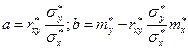 (32)
(32)
С учетом (32) уравнение регрессии Y на x может быть записано в виде:
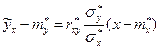 (33)
(33)
Аналогично, для регрессии X на y можно получить:
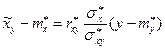 (34)
(34)
Число 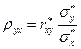 (35)
(35)
Называют коэффициентом регрессии Y на x.
Число 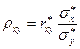 (36)
(36)
- коэффициент регрессии X на y.
Таким образом, нахождение эмпирической функции регрессии может быть сведено к вычислению коэффициентов регрессии 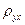 и
и 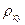 .
.
2. Задание.
Используя двумерную выборку своего варианта, выполнить:
- Составить корреляционную таблицу.
- Построить корреляционное поле.
- Найти выборочные функции регрессии (в табличной форме):
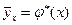 и
и 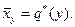
- Нанести выборочные линии регрессии на корреляционное поле (ломаная линия).
- Методом наименьших квадратов найти эмпирические функции линейной регрессии:
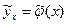 и
и 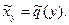
- Найти те же функции
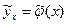 и
и 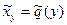 путем вычисления коэффициентов регрессии.
путем вычисления коэффициентов регрессии. - Нанести эмпирические функции регрессии на корреляционное поле.
3. Пример выполнения работы (решение варианта 0)
- Используя двумерную выборку варианта 0, составим корреляционную таблицу:
Таблица 5
| y x | 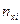
| |||||
| - | - | - | - | |||
| - | - | - | ||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | - | - | |||
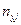
|
- Найдем минимальные и максимальные значения случайных величин X и y. Имеем
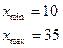
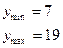
Корреляционное поле представляет собой изображение значений (вариантов) пар чисел в виде точек на плоскости. Корреляционное поле целесообразно строить на миллиметровой бумаге. На осях изобразить только тот промежуток, где находятся значения соответствующей случайной величины. Масштаб выбирается так, чтобы корреляционное поле заполнило целиком лист бумаги. Возле точек, изображающих двумерный вариант, проставить частоты этих вариантов. Корреляционное поле варианта 0 изображено на рис. 3.
- Для нахождения выборочных функций регрессии используем формулы (19) и (23).
Результаты вычислений сведем в таблицы:
Таблица 6
| X | ||||||
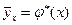
| 8, 71 | 13, 14 | 14, 4 | 15, 61 |
Таблица 7
| Y | |||||
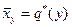
| 12, 5 | 25, 11 | 25, 2 | 29, 29 |
- Значения выборочных функций регрессии
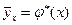 и
и 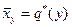 , содержащиеся в таблицах 6 и 7, изображаем в виде точек на корреляционном поле и соединяем последовательные точки отрезками прямых. Целесообразно выборочные функции регрессии изобразить разными цветами (см. рис.3).
, содержащиеся в таблицах 6 и 7, изображаем в виде точек на корреляционном поле и соединяем последовательные точки отрезками прямых. Целесообразно выборочные функции регрессии изобразить разными цветами (см. рис.3). - Для нахождения эмпирической функции регрессии Y на x необходимо решить систему линейных алгебраических уравнений (29) относительно неизвестных величин a и b. Предварительно необходимо вычислить коэффициенты при неизвестных (a и b) и свободные члены. Расчеты удобно свести в таблицу (см. таблицу 8).
Подставив коэффициенты и свободные члены в (29), получим:
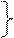
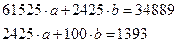 (36)
(36)
a и b находим по формулам Крамера.
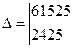
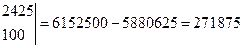
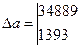
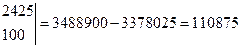
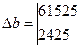
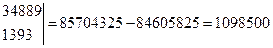
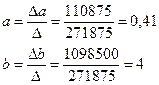 (37)
(37)
Таким образом эмпирическая функция регрессии Y на x имеет вид:
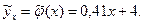 (38)
(38)
Проделав аналогичную работу, получим эмпирическую функцию регрессии X на y:
 (39)
(39)
4. Найдем те же функции 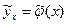 и
и 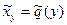 путем вычисления коэффициентов регрессии. Для этого воспользуемся формулами (9.1), (10.1), (11.2), (12.2), (15.1), (18),
путем вычисления коэффициентов регрессии. Для этого воспользуемся формулами (9.1), (10.1), (11.2), (12.2), (15.1), (18),
(32) – (36).
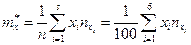
Таблица 8
| i | 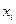
| 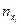
| 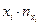
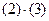
| 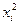
| 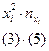
| 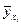
| 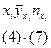
| 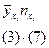
|
| 8, 71 | 914, 55 | 60, 97 | ||||||
| 13, 14 | 5518, 8 | 275, 94 | ||||||
| 14, 4 | 619, 2 | |||||||
| 15, 61 | 10770, 9 | 359, 03 | ||||||
| ∑ | 34889, 25 | 1393, 14 |
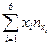
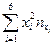

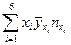




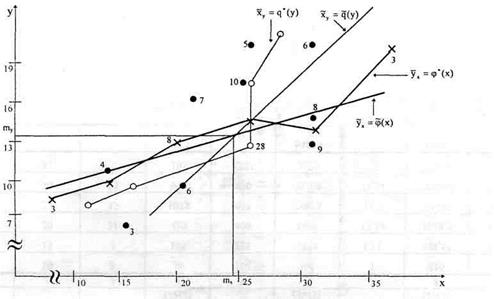
РИС. 3
Сумму 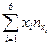 берем их из таблицы 8, получим
берем их из таблицы 8, получим 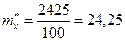 .
.
Аналогично:
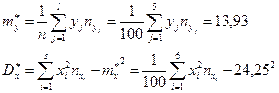
Сумму 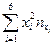 берем из таблицы 8, получим:
берем из таблицы 8, получим:
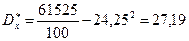
Аналогично:
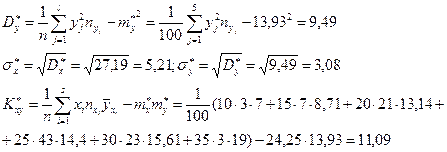
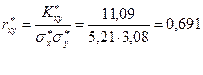
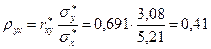
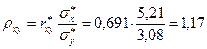
Используя формулы (33) и (34), запишем уравнения регрессии.
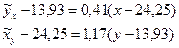
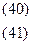
Чтобы убедиться в идентичности полученных результатов с эмпирическими функциями регрессии, полученным методом наименьших квадратов, разрешим выражения (40) и (41) относительно 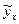 и
и 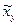 . Получим:
. Получим:
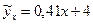 (42)
(42)
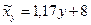 (43)
(43)
Сопоставляя выражения (42) и (43) с (38) и (39) соответственно, убеждаемся в правильности произведенных расчетов.
7.Изобразим графики эмпирических функций регрессии на корреляционном поле (см. рис. 3).
- Варианты исходных данных (выборок)
Вариант 0
| X | Y | X | Y | X | Y | X | Y | X | Y |
Вариант 1
| X | Y | X | Y | X | Y | X | Y | X | Y |
Вариант 2
| X | Y | X | Y | X | Y | X | Y | X | Y |
Вариант 3
| X | Y | X | Y | X | Y | X | Y | X | Y |
Вариант 4
| X | Y | X | Y | X | Y | X | Y | X | Y |
Вариант 5
| X | Y | X | Y | X | Y | X | Y | X | Y |
Вариант 6
| X | Y | X | Y | X | Y | X | Y | X | Y |
Вариант 7
| X | Y | X | Y | X | Y | X | Y | X | Y |
Вариант 8
| X | Y | X | Y | X | Y | X | Y | X | Y |
|