
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проверка значимости коэффициентов регрессии и всего уравнения в целом.
|
|
Этапы построения регрессионной модели, предпосылки регрессионного анализа.
1. Формулировка цели исследования, которая включает в себя отбор результативного показателя y и постановку задачи;
2. Отбор на содержательном уровне объясняющих переменных, оказывающих наибольшее влияние на результативный показатель y;
3. Сбор необходимой статистической информации, т.е. регистрация для каждого наблюдения значений результативного и объясняющих переменных, входящих в модель
4. Выбор вида функции регрессии f(X).
5. Идентификация модели. Оценивание неизвестных параметров регрессионной модели по исходным статистическим данным.
6. Верификация модели. Анализ адекватности модели, уровня согласованности исходных и модельных значений результативного показателя.
Предпосылки регрессионного анализа:
1. Зависимая переменная yi (возмущение ε i) – случайная величина, а объясняющая переменная xi – неслучайная величина
2. М(ε i)=0;
3. Дисперсия случайных остатков постоянна для любого i: D(ε i)=σ 2
4. Переменные ε i и ε j не коррелированы: M(ε i ε j)=0
5. Зависимая переменная yi (возмущение ε i) имеет нормальный закон распределения N(μ, σ)
Проверка значимости коэффициентов регрессии и всего уравнения в целом.
Проверка значимости уравнения регрессии т.е. гипотезы H0: β 1=0
Используется F-критерий, основанный на статистике:
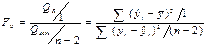
По таб.4 F-распределения Фишера-Снедекора находится Fкр (α; ν 1=1; ν 2=n-2).
Если Fн > Fкр, то гипотеза H0 отвергается с вероятностью ошибки и уравнение регрессии считается значимым.
Проверка значимости коэффициентов регрессии проводится по t-критерию. Нулевая гипотеза β i=0
Рассчитывается статистика
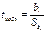
tкр = t (α; n-2).
Если наблюдаемое больше критического, то нулевая гипотеза отвергается, коэффициент значим.
Если меньше – не отвергается, коэффициент не значим.