Методы, используемые для оценки неизвестных параметров уравнения регрессии

Для нахождения оценок параметров уравнения регрессии чаще всего используется метод наименьших квадратов (МНК).

Обозначим оценки параметров уравнения регрессии β ₀ и β ₁ как b₀ и b₁.

В соответствии с методом наименьших квадратов (МНК) оценки b₀ и b₁ можно получить из условия минимизации суммы квадратов ошибок оценивания, т.е. минимизации суммы квадратов отклонений фактических значений зависимой переменной от расчетных ее значений, полученных на основе уравнения регрессии.

МНК: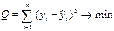

y_i – фактические значения зависимой переменной,

ŷ _i - расчётные значения, полученные на основе уравнения регрессии.

Разность 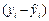называется остатком и дает количественную оценку значения ошибки, т.е. показывает воздействие возмущающей переменной.

МНК позволяет получить несмещённые оценки, а в случае линейной модели – оценки с минимальной дисперсией, дающие хорошее приближение оценок b_j к истинным значениям коэффициентов регрессии β _j.

Для оценки неизвестных параметров уравнения помимо МНК используют следующие критерии адекватности (функции потерь):

• Метод наименьших модулей;

• Метод минимакса.

Согласно МНМ минимизируется сумма абсолютных отклонений наблюдаемых значений результативного показателя 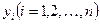от модельных значений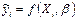

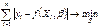
Получаемая регрессия называется среднеабсолютной (медианной).

Метод минимакса сводится к минимизации максимума модуля отклонения наблюдаемого значения результативного показателя 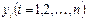от модельных значений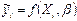

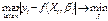
Получаемая регрессия называется минимаксной.